Слайд 21 способ графического решения уравнений с одним неизвестным
Пусть дано уравнение f(x)=g(x).
Приведем это

уравнение к виду f(x)-g(x)=0
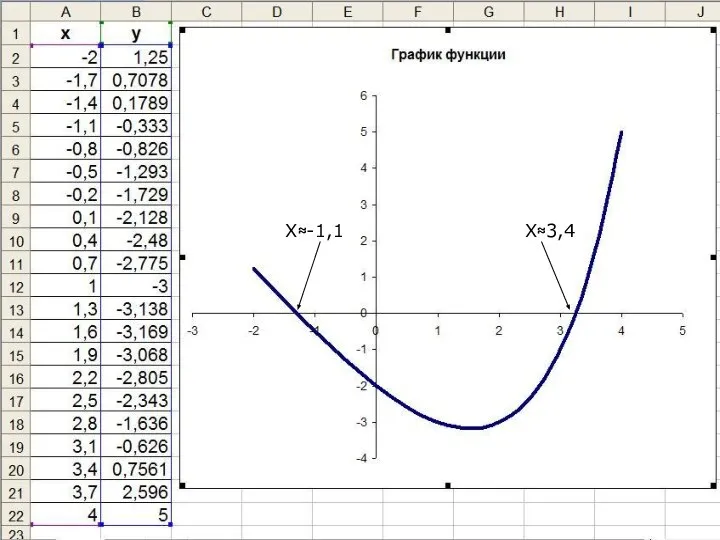
Введем функцию у=f(x)-g(x). Построим график этой функции
Количество точек пересечения графика с осью абсцисс дает число корней уравнения
Абсциссы точек пересечения и есть решения данного уравнения
Слайд 42 способ графического решения уравнений с одним неизвестным
Пусть дано уравнение f(x)=g(x).
Введем функции

у= f(x) и у =g(x).
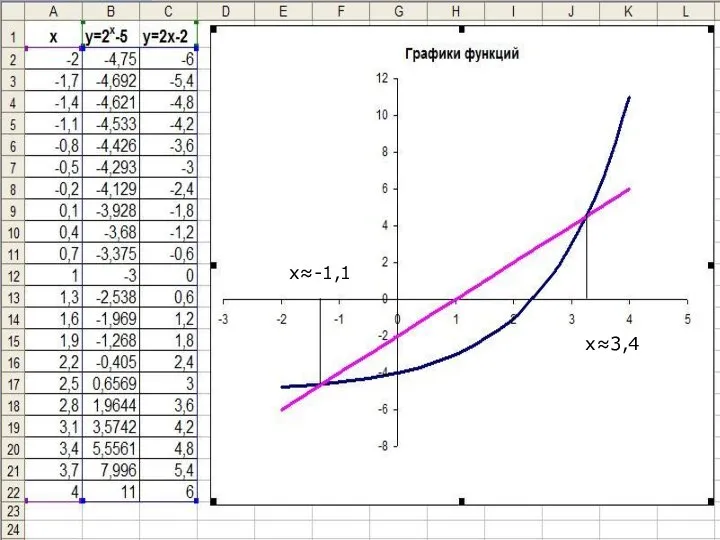
Построим графики этих функций в одной системе координат.
Количество точек пересечения дает число корней уравнения.
Абсциссы точек пересечения и есть решения данного уравнения.
Слайд 6
Алгоритм использования команды Подбор параметра:
Решить нужную задачу с каким – либо начальным

значение параметра;
Выбрать команду Подбор параметра в меню Сервис;
В появившемся окне диалога Подбор параметра в поле Установить в ячейке указывается адрес ячейки, значение в которой нужно изменить (такая ячейка называется целевой);
В поле Значение – то числовое значение, которое должно появиться в целевой ячейке;
В поле Изменяя значение ячейки ввести ссылку на ячейку с параметром
Слайд 7Использование надстройки Подбор параметра для 1 способа
По графику видно, что ближайший аргумент

к точке пересечения оси Х с графиком функции равен -1,1. По таблице значений функции можно определить, что этот аргумент функции хранится в ячейке А5
Выделить ячейку В5 со значением функции и выполним команду [Сервис-Подбор параметра….]
В диалоговом окне в поле Значение: ввести требуемое значение функции (0). В поле Изменяя значение ячейки: ввести адрес $A$5, в который будет производится подбор значения аргумента. Кнопка ОК
В ячейке аргумента A5 появится подобранное значение – 1,296. Корень уравнения найден с заданной точностью.
Слайд 8Графическое решение систем уравнений с двумя неизвестными
Пусть дана система уравнений
f(x,y)=0

и y(x,y)=0
1. Рассмотрим каждое из них в виде y=f(x) и y=u(x);
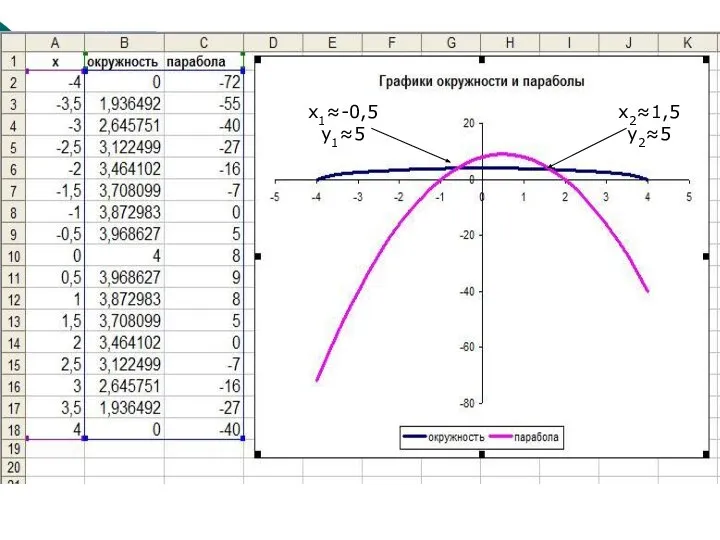
2. Построим эти кривые на одном графике;
3. Определим координаты точек их пересечения, что будет являться решением исходной системы уравнений.





 Действительные числа и преобразования алгебраических выражений (домашнее задание)
Действительные числа и преобразования алгебраических выражений (домашнее задание) Презентация на тему Цилиндр
Презентация на тему Цилиндр  Would you rather: thanksgiving edition
Would you rather: thanksgiving edition Теорема Пифагора. Чертеж к доказательству Пифагора
Теорема Пифагора. Чертеж к доказательству Пифагора Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Единицы, десятки
Единицы, десятки Лекция№7
Лекция№7 Координатная плоскость. (2). Игра Морской бой
Координатная плоскость. (2). Игра Морской бой Деление. Неправильные дроби
Деление. Неправильные дроби Порог чувствительности средства измерений
Порог чувствительности средства измерений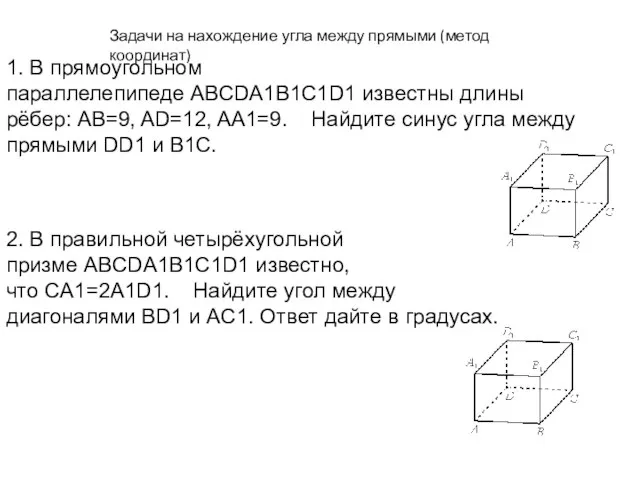 Задачи на нахождение угла между прямыми (метод координат)
Задачи на нахождение угла между прямыми (метод координат) Метод координат в пространстве
Метод координат в пространстве Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения Эконометрика. Цели преподавания дисциплины
Эконометрика. Цели преподавания дисциплины Дополнительные свойства вычисления пределов для дробно - рациональных функций
Дополнительные свойства вычисления пределов для дробно - рациональных функций Скрещивающиеся прямые
Скрещивающиеся прямые Презентация на тему Виды многогранников
Презентация на тему Виды многогранников  Весёлая математика. А ну-ка посчитай
Весёлая математика. А ну-ка посчитай Интегральное исчисление. Функция. Предел функции
Интегральное исчисление. Функция. Предел функции Треугольные узоры. Правильный треугольник
Треугольные узоры. Правильный треугольник Игра-тренажер. Веселая математика - геометрические фигуры
Игра-тренажер. Веселая математика - геометрические фигуры Функция y = x2 и её график
Функция y = x2 и её график Свойства функции
Свойства функции Математическая викторина В гостях у мудрой совы 2 класс
Математическая викторина В гостях у мудрой совы 2 класс Тетраэдр и параллелепипед. Геометрия 10 класс
Тетраэдр и параллелепипед. Геометрия 10 класс Чертёж призмы
Чертёж призмы Интегральная оценка угрозы биотерроризма. Цели, методы, задачи
Интегральная оценка угрозы биотерроризма. Цели, методы, задачи Правильные многоугольники
Правильные многоугольники