Содержание
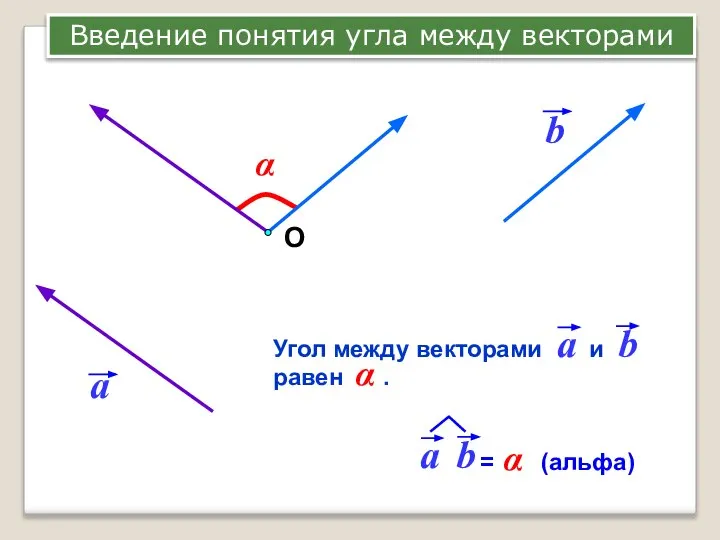
- 2. α О Введение понятия угла между векторами
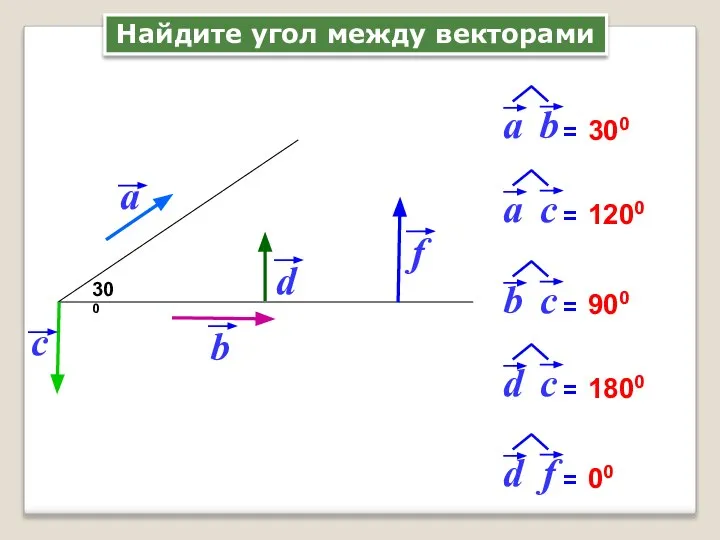
- 3. 300 300 1200 900 1800 00 Найдите угол между векторами
- 4. Скалярное произведение векторов – число (скаляр). Скалярным произведением двух векторов называется произведение их длин на косинус
- 5. = 0 Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
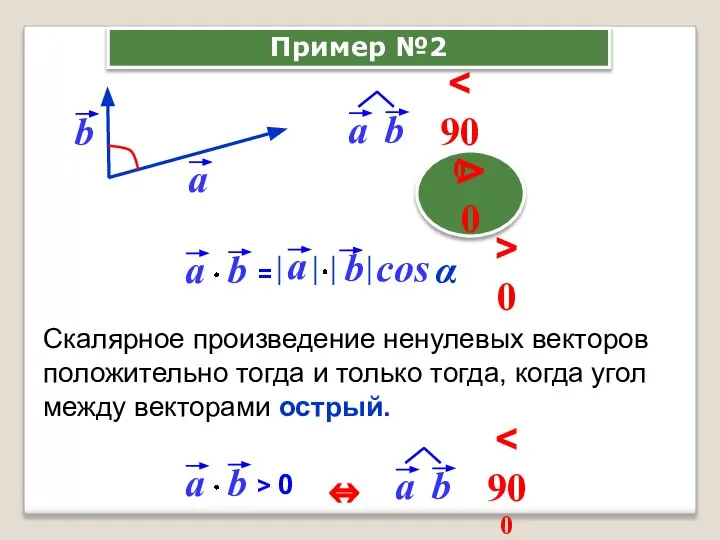
- 6. Скалярное произведение ненулевых векторов положительно тогда и только тогда, когда угол между векторами острый. cos α
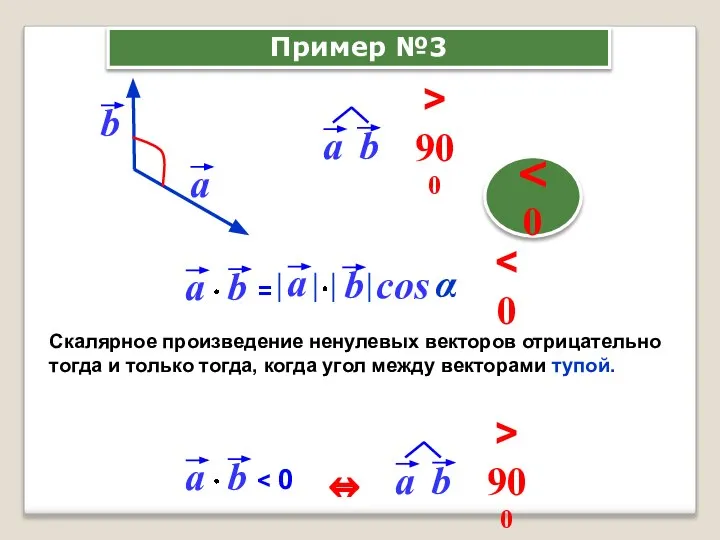
- 7. Скалярное произведение ненулевых векторов отрицательно тогда и только тогда, когда угол между векторами тупой. cos α
- 8. cos 00 1 cos1800 -1 Пример №4
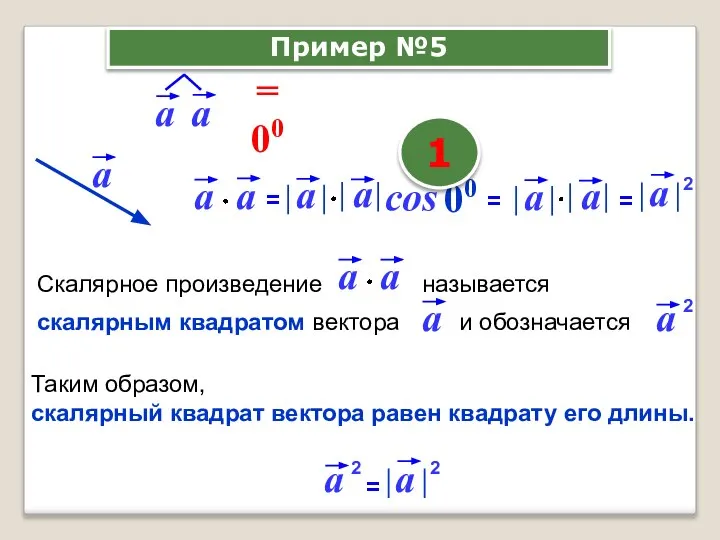
- 9. cos 00 1 Таким образом, скалярный квадрат вектора равен квадрату его длины. Пример №5 2 2
- 10. ИТОГО: – скалярный квадрат вектора
- 13. Скалярное произведение двух векторов равно сумме произведений их соответствующих координат.
- 14. б) решите самостоятельно
- 16. Скачать презентацию








 Деление обыкновенных дробей
Деление обыкновенных дробей Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 3
Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 3 Касательная к окружности. 8 класс
Касательная к окружности. 8 класс Путь и перемещение
Путь и перемещение Презентация на тему Умножение десятичных дробей на натуральные числа
Презентация на тему Умножение десятичных дробей на натуральные числа  Деление суммы на число
Деление суммы на число Обобщение. Высказывания. Ориентирование на местности
Обобщение. Высказывания. Ориентирование на местности Интерактивная игра для детей дошкольного возраста Путешествие в страну Математика
Интерактивная игра для детей дошкольного возраста Путешествие в страну Математика Подготовка к блиц-турниру
Подготовка к блиц-турниру Таблицы умножения и деления на 2 и 3
Таблицы умножения и деления на 2 и 3 Множення десяткових дробів. 5 клас
Множення десяткових дробів. 5 клас Степенная функция и её график
Степенная функция и её график Многогранники. Розв'язування задач
Многогранники. Розв'язування задач Обыкновенные дифференциальные уравнения. Вариант 4
Обыкновенные дифференциальные уравнения. Вариант 4 Решение уравнений (урок 3). 6 класс
Решение уравнений (урок 3). 6 класс Понятия и свойства функции. Предел функции
Понятия и свойства функции. Предел функции Число 0. Цифра 0
Число 0. Цифра 0 Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии Теорема Пифагора
Теорема Пифагора Презентация на тему Изображение пространственных фигур
Презентация на тему Изображение пространственных фигур 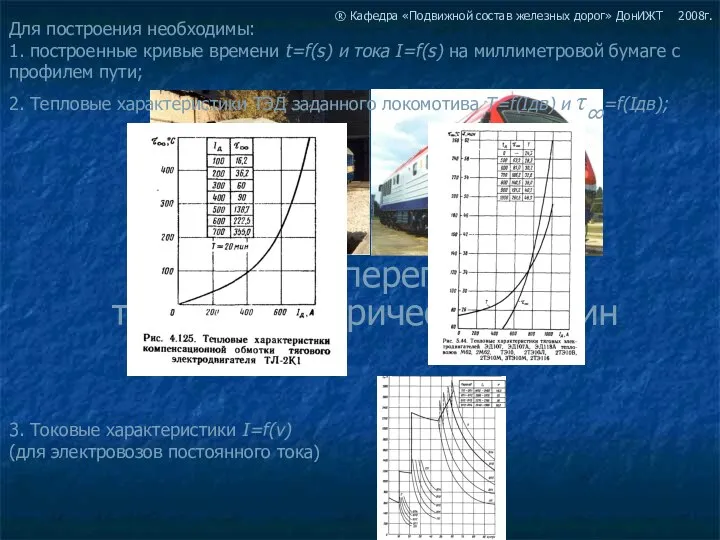 Расчет перегрева тяговых электрических машин
Расчет перегрева тяговых электрических машин Степенные функции, их свойства и графики
Степенные функции, их свойства и графики Введение в фармакологию
Введение в фармакологию Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Функции и их графики
Функции и их графики Производная произведения. Производная частного
Производная произведения. Производная частного Сечение куба, призмы, пирамиды
Сечение куба, призмы, пирамиды Параллельный перенос и поворот
Параллельный перенос и поворот