обратные тригонометрические функции

Содержание
Функция y = arcsin x и ее свойства
Функция y = arccos x и ее свойства
Функция y = arctg x и ее свойства
Функция y = arcctg x и ее свойства

Функция y=arcsin x и ее свойства
Если |а| ‌‌≤ 1, то arcsin а – это такое число из отрезка [-π/2; π/2], синус которого равен а.

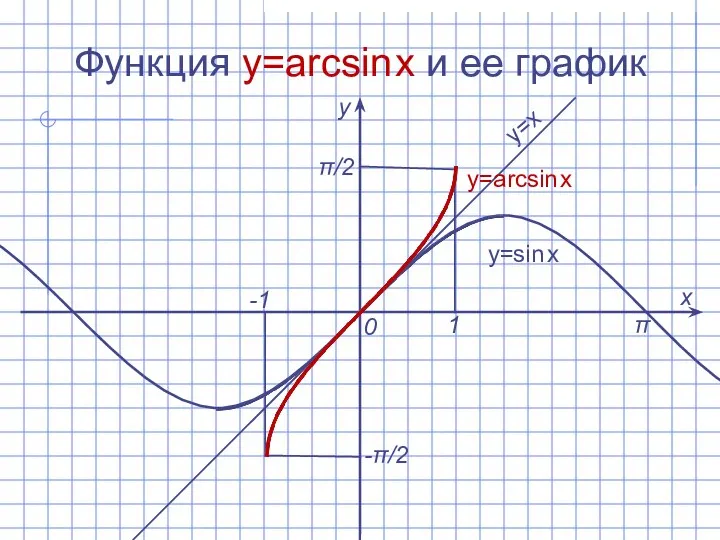
Функция y=arcsin x и ее график
х
у
0
1
-1
y=arcsin x
y=x
y=sin x
π/2
-π/2
π

Функция y=arcsin x и ее свойства
D(y) = [-1; 1].
E(y) = [-π/2; π/2].
arcsin (-x) = - arcsin x – функция нечетная.
Функция возрастает на [-1; 1].
Функция непрерывна.

Функция y=arccos x и ее свойства
Если |а| ‌‌≤ 1, то arccos а – это такое число из отрезка [0; π], косинус которого равен а.

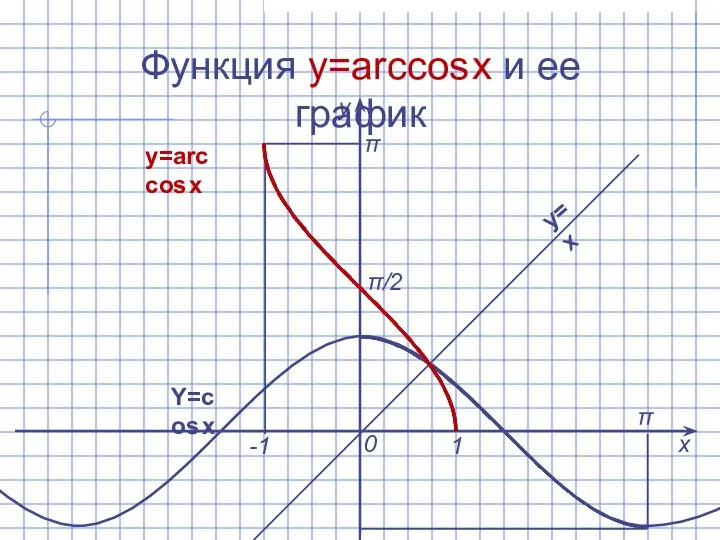
Функция y=arccos x и ее график
х
у
0
1
-1
π
y=arccos x
y=x
Y=cos x
π/2
π

Функция y=arccos x и ее свойства
D(y) = [-1; 1].
E(y) = [0; π].
Функция не является ни четной, ни нечетной.
Функция убывает на [-1; 1].
Функция непрерывна.

Функция y=arctg x и ее свойства
arctg а – это такое число из интервала (-π/2; π/2), тангенс которого равен а.

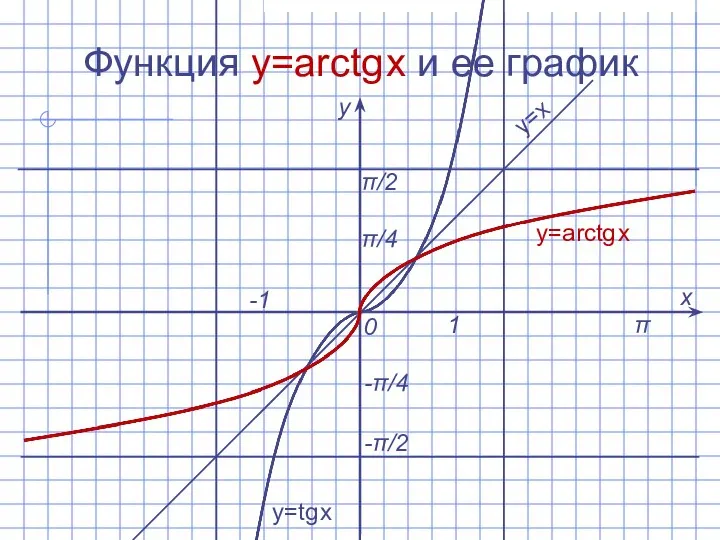
Функция y=arctg x и ее график
х
у
0
1
-1
y=arctg x
y=x
y=tg x
π/2
-π/2
π
π/4
-π/4

Функция y=arctg x и ее свойства
D(y) = (- ∞; +∞).
E(y) = (-π/2; π/2).
arctg (-x) = - arctg x – функция нечетная.
Функция возрастает на (- ∞; +∞).
Функция непрерывна.

Функция y=arcctg x и ее свойства
arcсtg а – это такое число из интервала (0; π), котангенс которого равен а.

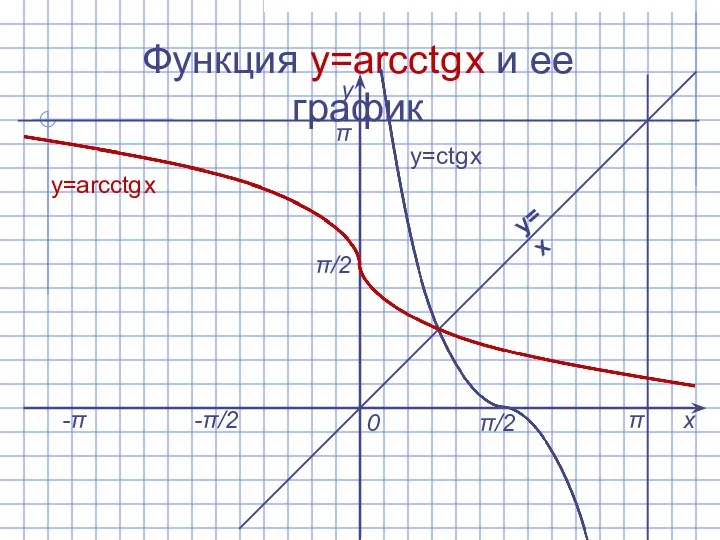
Функция y=arcctg x и ее график
х
у
0
y=arcсtg x
y=x
y=сtg x
-π/2
π/2
π
π/2
π
-π