Слайд 2Тема урока
Применение производной при решении
задач ЕГЭ

Слайд 3«Лишь дифференциальное исчисление даёт естествознанию возможность изображать математически не только состояния, но

и процессы движения.» Ф. Энгельс
Слайд 4Общие задания:
Зачем нужна производная?
2. Где мы встречаемся с производной и используем её?
3.

Можно ли без неё обойтись в математике и не только?
Слайд 5Вывод:
Производная - одно из самых важных понятий математического анализа. Знание производной необходимо

инженерам-технологам, конструкторам, экономистам, физикам, учёным.
Слайд 6Устный счёт.
По карточкам в парах проверяем основные формулы дифференцирования функций.
2. Находим производные

представленных функций.
Слайд 7Найти производную:
f(x) = cos 3x 2) f(x) = 4x3 –x2
3) f(x)

= е2х 4) f(x) = 2x
5) f(x) = ln (5-x) 6) f(x) = 12 sin 3 x
7) f(x) = 78 π x 8)(4х-2)3
Слайд 8Ответы:
1. -3sin3х
2. 12х2-2х
3. 2е2х
4. 2
5. - 1/(5-х)
6. 36cos3х
7. 12(4х-2) 2

Слайд 9Задания по группам:
1 группа: Применение производной для нахождения наибольшего и наименьшего значений

функции на указанном промежутке.
Слайд 10Задания по группам:
2 группа: Применение производной для нахождения наибольшего и наименьшего значений

функции без указания числового промежутка.
Слайд 11Задания по группам:
3 группа: Применение производной для нахождения точек экстремума функции.

Слайд 12Физ.пауза.
1.Наклон головы вперёд-назад.
2.Наклон головы влево- вправо.
3.Описать головой полукруг.
4.Руки вперёд, кисти «замком»,

повороты сцепленными руками влево- вправо.
5.Руки вниз, поднимаем и опускаем плечи.
Слайд 13Работа в группах
Найти наименьшее значение функции у=(х2+25)/х на отрезке (-10;-1)

Слайд 15Работа в группах
Определите точку минимума функции
У=(2х2-16х+16)е28-х

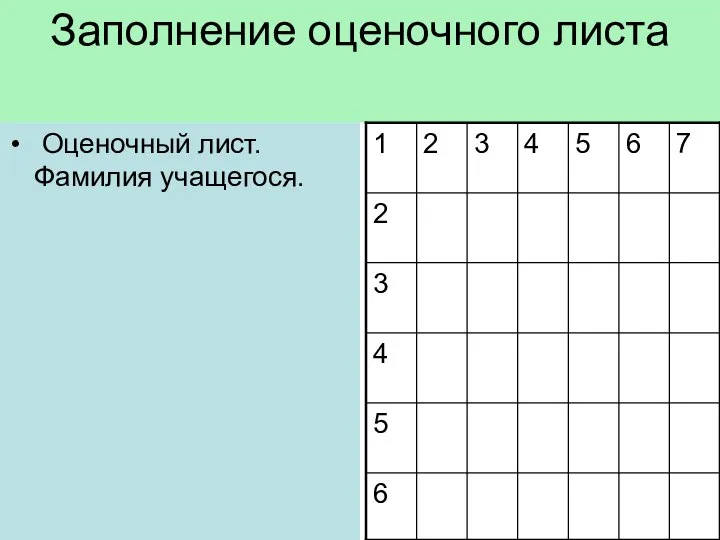
Слайд 17Заполнение оценочного листа
Оценочный лист. Фамилия учащегося.
















 Число 10
Число 10 Сумма углов в треугольнике
Сумма углов в треугольнике Перестановочные тесты и бутстреп анализ
Перестановочные тесты и бутстреп анализ Старинные меры длины на Руси
Старинные меры длины на Руси Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью
Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью Устный счёт для дошкольников
Устный счёт для дошкольников Расчёт надёжности систем с использованием экспоненциального закона распределения функции надёжности
Расчёт надёжности систем с использованием экспоненциального закона распределения функции надёжности Графическое решение уравнений
Графическое решение уравнений Презентация на тему Типы параллелепипеда
Презентация на тему Типы параллелепипеда  Первый признак равенства треугольников. 7 класс
Первый признак равенства треугольников. 7 класс Трапеция. Задачи по готовым чертежам
Трапеция. Задачи по готовым чертежам Морфизмы алгебр
Морфизмы алгебр Дополни до 10
Дополни до 10 Решение уравнений (2 класс)
Решение уравнений (2 класс) Задачи. вариант 3
Задачи. вариант 3 Презентация на тему Дроби и проценты
Презентация на тему Дроби и проценты  Стереометрические задачи повышенной сложности
Стереометрические задачи повышенной сложности Векторы
Векторы Свойства и графики тригонометрических функций
Свойства и графики тригонометрических функций Взаимное пересечение двух поверхностей. Лекция 9
Взаимное пересечение двух поверхностей. Лекция 9 Начальные понятия геометрии
Начальные понятия геометрии Применение метода интервалов для решения неравенств. 8 класс
Применение метода интервалов для решения неравенств. 8 класс Конструирование пирамиды. Пирамиды в архитектуре и в повседневной жизни
Конструирование пирамиды. Пирамиды в архитектуре и в повседневной жизни Преобразование обыкновенных дробей в десятичные
Преобразование обыкновенных дробей в десятичные Числа 1,2. Цифры 1,2
Числа 1,2. Цифры 1,2 Теорія ймовірностей, ймовірнісні процеси і математична статистика
Теорія ймовірностей, ймовірнісні процеси і математична статистика Презентация на тему Арифметические действия с десятичными дробями
Презентация на тему Арифметические действия с десятичными дробями 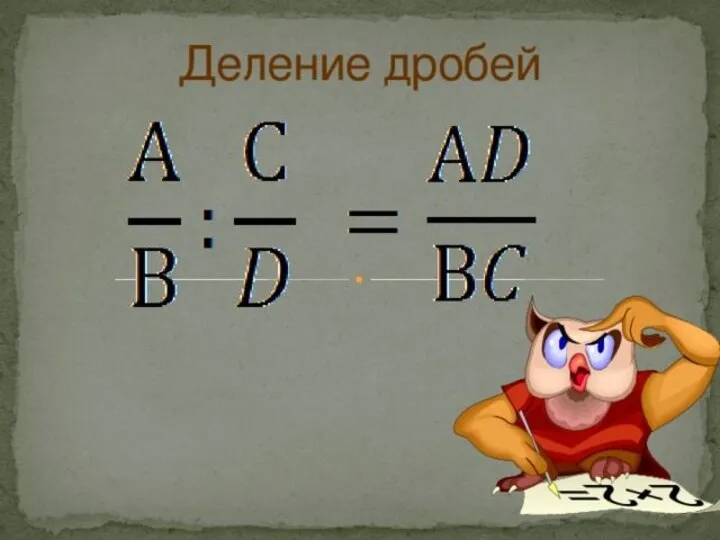 Деление дробей
Деление дробей