Aproximarea numerică a funcţiilor. Metode numerice – curs 11

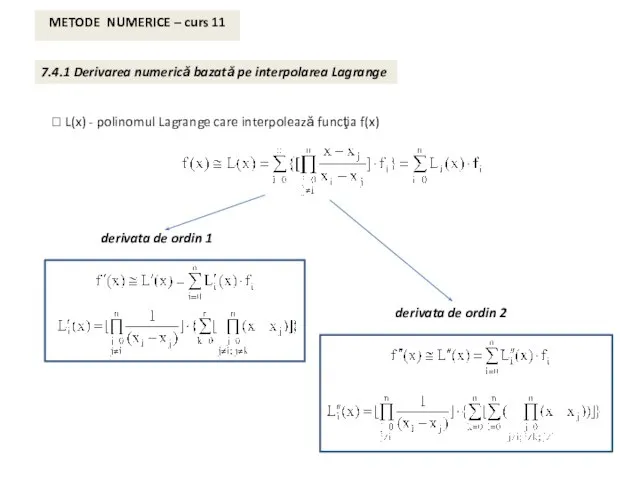
METODE NUMERICE – curs 11
7.4.1 Derivarea numerică bazată pe interpolarea Lagrange
⮚ L(x) - polinomul Lagrange care interpolează funcţia f(x)
derivata de ordin 1
derivata de ordin 2

METODE NUMERICE – curs 11
7.4.2 Formule de derivare numerică bazate pe interpolarea cu funcţii spline cubice
⮚ pentru aproximarea derivatelor de ordin superior, se folosesc funcţii spline de ordin mai mare decât 3 pentru aproximarea funcţiei f

METODE NUMERICE – curs 11
7.5 Cuadratura numerică
⮚ problema de calculul → determinarea valoarii integralei definite
⮚ spre deosebire de operaţia de derivare numerică, cuadratura tinde să “netezească” sau să diminueze erorile ce afectează datele.
Definiţii:
✧ Se numeşte regulă (elementară) de cuadratură, o formulă simplă care aproximează valorile integralelor elementare .
✧ Se numeşte regulă compusă de cuadratură, o formulă care aproximează valoarea integralei definite , ca o sumă a regulilor (elementare) de cuadratură.

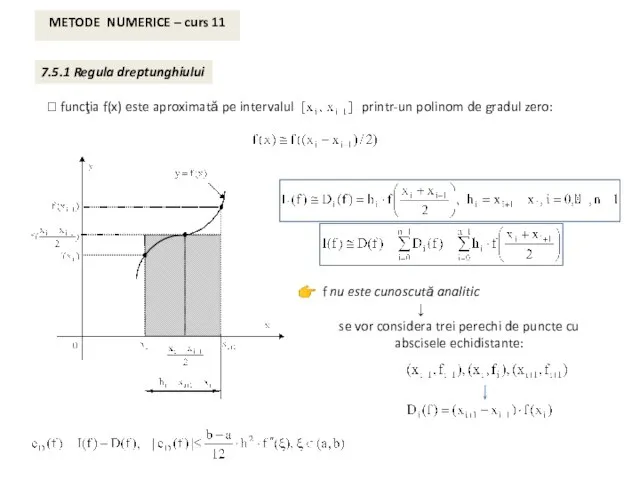
METODE NUMERICE – curs 11
7.5.1 Regula dreptunghiului
f nu este cunoscută analitic
↓
se vor considera trei perechi de puncte cu abscisele echidistante:

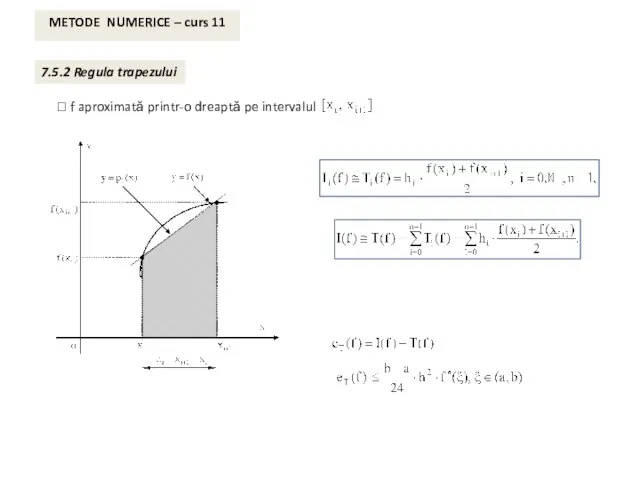
METODE NUMERICE – curs 11
7.5.2 Regula trapezului
⮚ f aproximată printr-o dreaptă pe intervalul

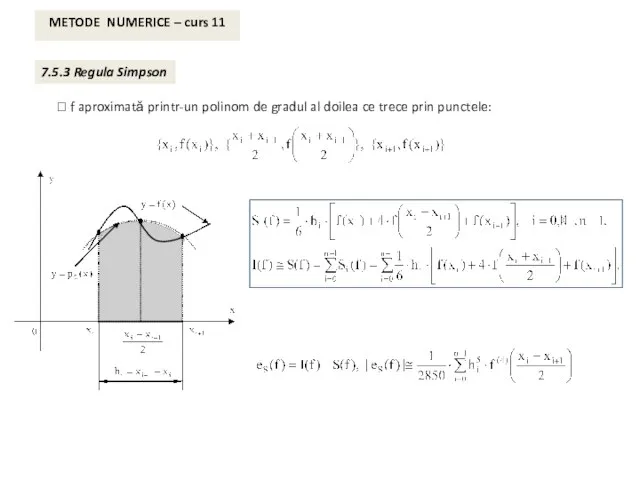
METODE NUMERICE – curs 11
7.5.3 Regula Simpson
⮚ f aproximată printr-un polinom de gradul al doilea ce trece prin punctele:

METODE NUMERICE – curs 11
f nu este cunoscută analitic
↓
se vor considera trei perechi de puncte cu abscisele echidistante:
? se consideră divizarea intervalului [a, b] ca fiind formată din puncte echidistante:
dezvoltări particulare:
▪ n - impar
▪ n - par
regula 1/3 Simpson
regula 3/8 Simpson

METODE NUMERICE – curs 11
7.5.4 Cuadratura bazată pe interpolarea cu funcţii spline cubice
⮚ se utilizează rezultatele aproximării funcţiei f prin interpolare cu funcţii spline cubice (naturale)
? ţinând cont de expresiile coeficienţilor ai, bi, ci, di:
faţă de formula trapezului, apare în plus termenul
creşte precizia aproximării

METODE NUMERICE – curs 11
Cap. 8 Ecuaţii diferenţiale ordinare cu condiţii iniţiale
8.1 Formularea problemei
8.1.1 Ecuaţii diferenţiale ordinare de ordinul întâi
⮚ fie o funcţie reală de două variabile reale:
- variabilă independentă
- variabilă dependentă
⮚ se consideră ecuaţia diferenţială de ordinul întâi de forma:
condiţia iniţială
⮚ Problema de calcul → determinarea soluţiei (aproximative), y(t), a ecuaţiei diferenţiale (1), cu condiţia iniţială (2), pentru orice valoare a argumentului
(1)
(2)
problema Cauchy

METODE NUMERICE – curs 11
Teoremă:
Fie ecuaţia (1) şi condiţia iniţială (2). Dacă sunt îndeplinite condiţiile:
funcţia f este continuă în raport cu argumentul ;
funcţia f este lipschitziană în raport cu argumentul , anume astfel încât este îndeplinită relaţia:
atunci există şi este unică o soluţie a problemei Cauchy.
? metodele numerice de rezolvare a problemei Cauchy discretizează intervalul [a,b] într-o reţea de puncte distincte şi anume:
? prin anumite formule de recurenţă se calculează yi, drept aproximaţii ale soluţiei exacte y(ti), având drept punct de start valoarea precizată y0:
soluţia numerică a problemei Cauchy
paşi de integrare
pas de observare

METODE NUMERICE – curs 11
8.1.2 Ecuaţii diferenţiale ordinare de ordin superior
? ecuaţii diferenţiale ordinare de ordinul n
condiţiile iniţiale cunoscute
cunoscută analitic sau printr-un şir de valori
? pentru rezolvarea numerică a acestei ecuaţii → se transformă într-un sistem de n ecuaţii diferenţiale ordinare, fiecare ecuaţie fiind de ordinul întâi
↓
metodele pentru rezolvarea ecuaţiilor diferenţiale de ordinul întâi se extind la cazul sistemelor de ecuaţii diferenţiale
(3)

METODE NUMERICE – curs 11
? ecuaţia (3) se rescrie sub forma:
? notaţii:
? se definesc urmoarele variabile de lucru: