позволяет значительно упростить вычисление криволинейного интеграла.
Формула Остроградского – Грина устанавливает связь между криволинейным интегралом и двойным интегралом, т.е. дает выражение интеграла по замкнутому контуру через двойной интеграл по области, ограниченной этим контуром.
Будем считать, что рассматриваемая область односвязная, т.е. в ней нет исключенных участков.
Если участки АВ и CD контура принять за произвольные кривые, то, проведя соответствующие преобразования, получим формулу для контура произвольной формы:
Область, ограниченная
контуром








 Угол между прямыми
Угол между прямыми Неопределённый интеграл
Неопределённый интеграл Вычисление площадей и объемов. Лекция 5
Вычисление площадей и объемов. Лекция 5 Прямоугольный параллелепипед
Прямоугольный параллелепипед Построение цилиндра в изометрической проекции
Построение цилиндра в изометрической проекции Построение графика функции
Построение графика функции Ряд Тейлора функции многих переменных. Лекция 19
Ряд Тейлора функции многих переменных. Лекция 19 Презентация на тему Решение задач В10 (ЕГЭ 2012)
Презентация на тему Решение задач В10 (ЕГЭ 2012)  Преобразование рациональных выражений
Преобразование рациональных выражений Биматричные игры
Биматричные игры Сочетательное и распределительное свойство умножения. Урок 1
Сочетательное и распределительное свойство умножения. Урок 1 Математическая игра Счастливое число 7!
Математическая игра Счастливое число 7!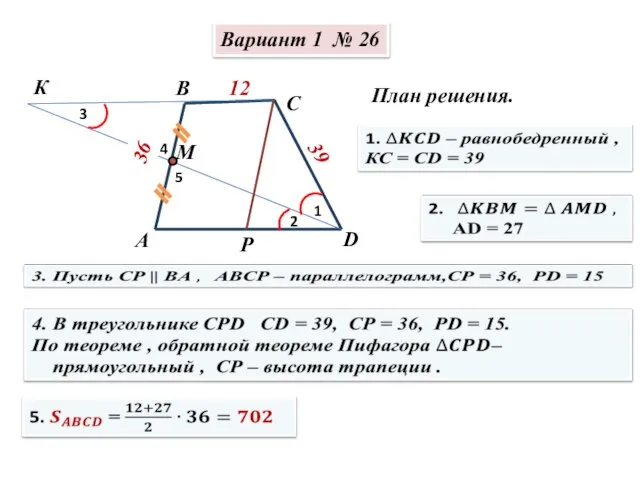 Сборник И.В. Ященко. Решение заданий №26
Сборник И.В. Ященко. Решение заданий №26 Сложение и вычитание. Закрепление. Урок математики, 1 класс
Сложение и вычитание. Закрепление. Урок математики, 1 класс Сравнение множеств. Отображения множеств
Сравнение множеств. Отображения множеств Луч. Отрезок. Путешествие точки
Луч. Отрезок. Путешествие точки Презентация на тему Биссектриса угла в треугольнике
Презентация на тему Биссектриса угла в треугольнике  08_ ОТС_ Основы теории СП-2
08_ ОТС_ Основы теории СП-2 Сложение и вычитание многочленов
Сложение и вычитание многочленов Чётность и нечётность, периодичность тригонометрических функций с изменениями
Чётность и нечётность, периодичность тригонометрических функций с изменениями Случаи вычитания 17 -
Случаи вычитания 17 - Интерактивный тест Степень. Свойства степени
Интерактивный тест Степень. Свойства степени Модели пирамид
Модели пирамид Математика задача. Решение задачи уч. Стр.92 №2
Математика задача. Решение задачи уч. Стр.92 №2 Математика в профессии повара
Математика в профессии повара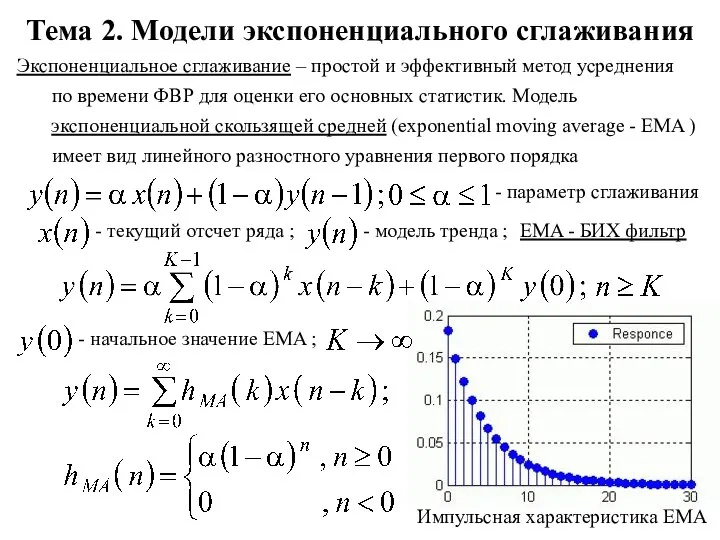 Модели экспоненциального сглаживания. Тема 2
Модели экспоненциального сглаживания. Тема 2 Презентация на тему Касательная к графику функции
Презентация на тему Касательная к графику функции  Треугольник. Виды треугольников
Треугольник. Виды треугольников