- Главная
- Математика
- Применение теории графов

Содержание
- 2. Развитие теории графов в основном обязано большому числу всевозможных приложений. По-видимому, из всех математических объектов графы
- 3. ГРАФЫ И ХИМИЯ За последние десятилетия в теоретической химии широкое распространение получили представления топологии и теории
- 4. ГРАФЫ И БИОЛОГИЯ Элементы теории графов используются и в экологии. Природные сообщества обладают сложным строением: несколькими
- 5. ГРАФЫ И ИНФОРМАЦИЯ Двоичные деревья играют весьма важную роль в теории информации. Предположим, что определенное число
- 6. ГРАФЫ И ФИЗИКА Еще недавно одной из наиболее сложных и утомительных задач для радиолюбителей было конструирование
- 7. ГРАФЫ И ТРАНСПОРТ Теория графов находит широкое применение в транспортных и коммуникационных системах. Приведём пример, связанный
- 8. ГРАФЫ И ТРАНСПОРТ Кроме обработки входящих запросов и нахождения области местоположения на основе координат пользователя, а
- 9. ГРАФЫ И ТРАНСПОРТ Представим этот сегмент в виде графа. Это неориентированный взвешенный граф. Чтобы найти кратчайший
- 10. ГРАФЫ И ТРАНСПОРТ Алгоритм действий Отметим все вершины непосёщенными. Присвоим каждой вершине значение расстояния до неё.
- 12. Скачать презентацию
Слайд 2Развитие теории графов в основном обязано большому числу всевозможных приложений. По-видимому, из
Развитие теории графов в основном обязано большому числу всевозможных приложений. По-видимому, из

Графы нашли применение практически во всех отраслях научных знаний: физике, биологии, химии, математике, истории, лингвистике, социальных науках, технике и т.п. Наибольшей популярностью теоретико-графовые модели используются при исследовании коммуникационных сетей, систем информатики, химических и генетических структур, электрических цепей и других систем сетевой структуры.
Слайд 3ГРАФЫ И ХИМИЯ
За последние десятилетия в теоретической химии широкое распространение получили представления
ГРАФЫ И ХИМИЯ
За последние десятилетия в теоретической химии широкое распространение получили представления
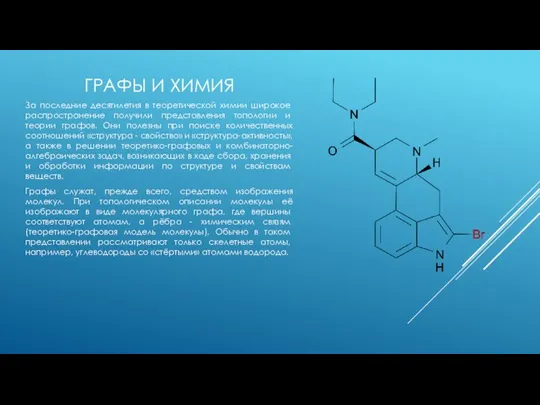
Графы служат, прежде всего, средством изображения молекул. При топологическом описании молекулы её изображают в виде молекулярного графа, где вершины соответствуют атомам, а рёбра - химическим связям (теоретико-графовая модель молекулы). Обычно в таком представлении рассматривают только скелетные атомы, например, углеводороды со «стёртыми» атомами водорода.
Слайд 4ГРАФЫ И БИОЛОГИЯ
Элементы теории графов используются и в экологии. Природные сообщества обладают
ГРАФЫ И БИОЛОГИЯ
Элементы теории графов используются и в экологии. Природные сообщества обладают
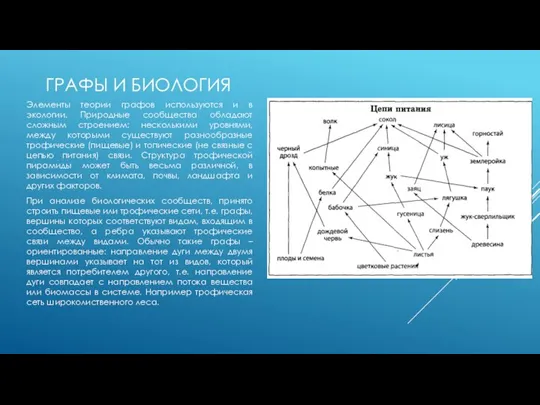
При анализе биологических сообществ, принято строить пищевые или трофические сети, т.е. графы, вершины которых соответствуют видам, входящим в сообщество, а ребра указывают трофические связи между видами. Обычно такие графы – ориентированные: направление дуги между двумя вершинами указывает на тот из видов, который является потребителем другого, т.е. направление дуги совпадает с направлением потока вещества или биомассы в системе. Например трофическая сеть широколиственного леса.
Слайд 5ГРАФЫ И ИНФОРМАЦИЯ
Двоичные деревья играют весьма важную роль в теории информации. Предположим,
ГРАФЫ И ИНФОРМАЦИЯ
Двоичные деревья играют весьма важную роль в теории информации. Предположим,

Двоичные кодовые деревья допускают интерпретацию в рамках теории поиска. Каждой вершине при этом сопоставляется вопрос, ответить на который можно либо "да", либо "нет". Утвердительному и отрицательному ответу соответствуют два ребра, выходящие из вершины. "Опрос" завершается, когда удается установить то, что требовалось.
Таким образом, если кому-то понадобится взять интервью у различных людей, и ответ на очередной вопрос будет зависеть от заранее неизвестного ответа на предыдущий вопрос, то план такого интервью можно представить в виде двоичного дерева.
Слайд 6ГРАФЫ И ФИЗИКА
Еще недавно одной из наиболее сложных и утомительных задач для
ГРАФЫ И ФИЗИКА
Еще недавно одной из наиболее сложных и утомительных задач для

Печатной схемой называют пластинку из какого-либо диэлектрика (изолирующего материала), на которой в виде металлических полосок вытравлены дорожки. Пересекаться дорожки могут только в определенных точках, куда устанавливаются необходимые элементы (диоды, триоды, резисторы и другие), их пересечение в других местах вызовет замыкание электрической цепи.
В ходе решения этой задачи необходимо вычертить плоский граф, с вершинами в указанных точках.
Слайд 7ГРАФЫ И ТРАНСПОРТ
Теория графов находит широкое применение в транспортных и коммуникационных системах.
ГРАФЫ И ТРАНСПОРТ
Теория графов находит широкое применение в транспортных и коммуникационных системах.
Серверная часть должна обрабатывать миллионы пользовательских запросов, отправляя каждый из запросов одному или нескольким водителям поблизости. Хоть проще и иногда даже рациональнее отправлять запрос пользователя всем водителями, находящимся поблизости, всё же потребуется предварительная обработка.
Слайд 8ГРАФЫ И ТРАНСПОРТ
Кроме обработки входящих запросов и нахождения области местоположения на основе
ГРАФЫ И ТРАНСПОРТ
Кроме обработки входящих запросов и нахождения области местоположения на основе
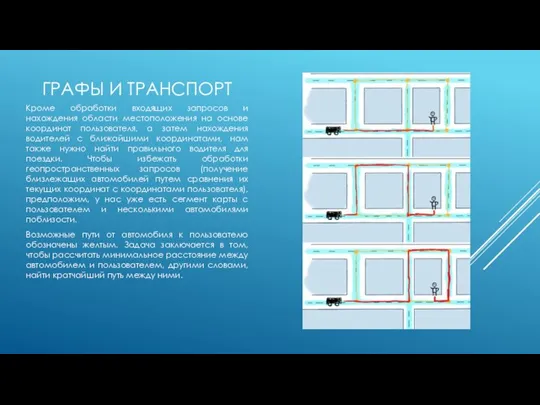
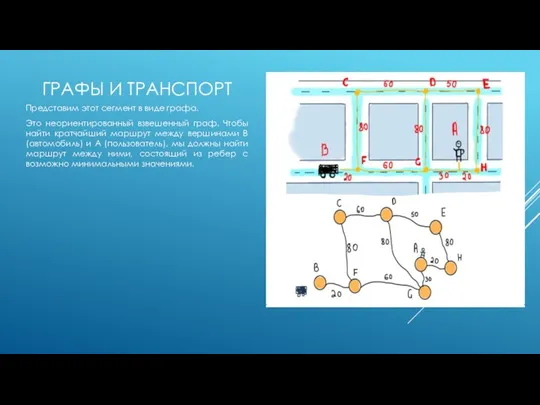
Возможные пути от автомобиля к пользователю обозначены желтым. Задача заключается в том, чтобы рассчитать минимальное расстояние между автомобилем и пользователем, другими словами, найти кратчайший путь между ними.
Слайд 9ГРАФЫ И ТРАНСПОРТ
Представим этот сегмент в виде графа.
Это неориентированный взвешенный граф. Чтобы
ГРАФЫ И ТРАНСПОРТ
Представим этот сегмент в виде графа.
Это неориентированный взвешенный граф. Чтобы
Слайд 10ГРАФЫ И ТРАНСПОРТ
Алгоритм действий
Отметим все вершины непосёщенными.
Присвоим каждой вершине значение расстояния до
ГРАФЫ И ТРАНСПОРТ
Алгоритм действий
Отметим все вершины непосёщенными.
Присвоим каждой вершине значение расстояния до
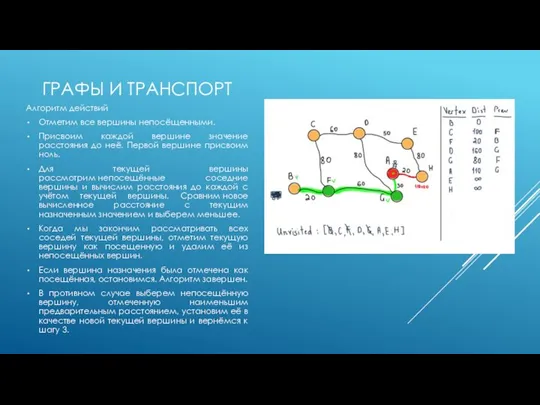
Для текущей вершины рассмотрим непосещённые соседние вершины и вычислим расстояния до каждой с учётом текущей вершины. Сравним новое вычисленное расстояние с текущим назначенным значением и выберем меньшее.
Когда мы закончим рассматривать всех соседей текущей вершины, отметим текущую вершину как посещенную и удалим её из непосещённых вершин.
Если вершина назначения была отмечена как посещённая, остановимся. Алгоритм завершен.
В противном случае выберем непосещённую вершину, отмеченную наименьшим предварительным расстоянием, установим её в качестве новой текущей вершины и вернёмся к шагу 3.
 Геометрический конструктор: Развивающая игра Танграм
Геометрический конструктор: Развивающая игра Танграм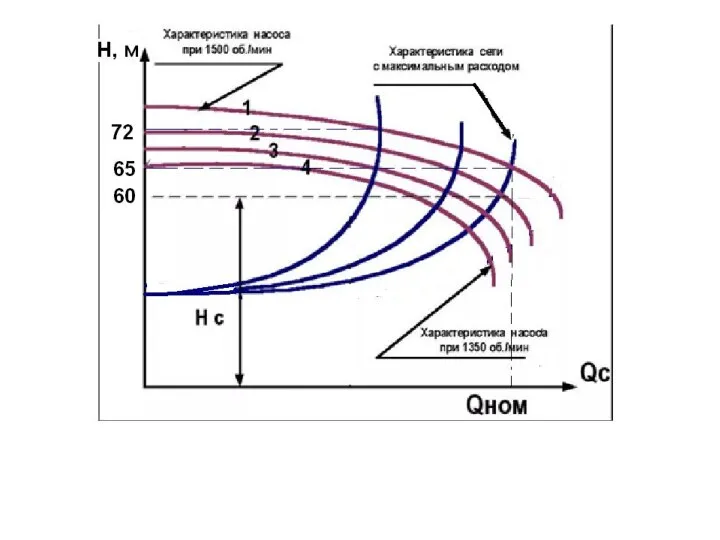 Модель частотно-регулируемого привода. (Тема 8)
Модель частотно-регулируемого привода. (Тема 8) Веселый счет. Викторина
Веселый счет. Викторина Производная сложной функции
Производная сложной функции Старинные задачи с использованием дробей
Старинные задачи с использованием дробей Обобщение и систематизация знаний и умений по теме Взаимное расположение прямых в пространстве. Параллельные прямые
Обобщение и систематизация знаний и умений по теме Взаимное расположение прямых в пространстве. Параллельные прямые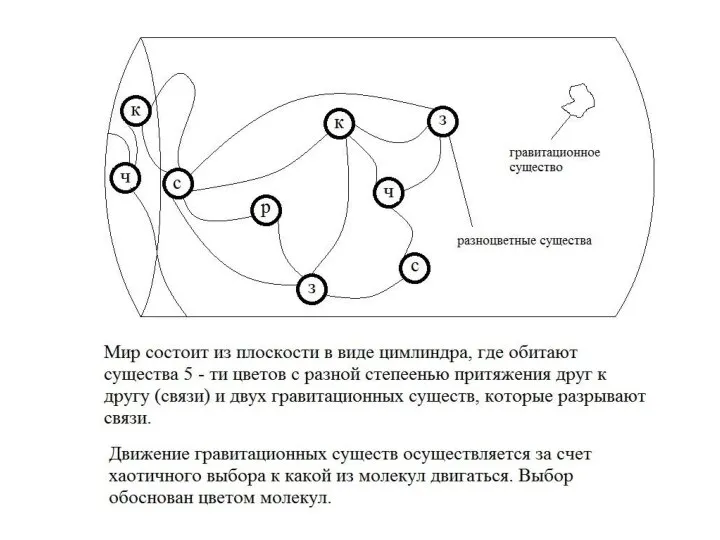 Мир в поверхности цилиндра
Мир в поверхности цилиндра Сложение чисел с разными знаками
Сложение чисел с разными знаками Многоугольники. Их формы
Многоугольники. Их формы Синус, косинус, тангенс и котангенс
Синус, косинус, тангенс и котангенс Развёртка куба
Развёртка куба Математика в танце
Математика в танце Линейное уравнение с одной переменной (7 класс)
Линейное уравнение с одной переменной (7 класс) Прямоугольник. Квадрат. Периметр многоугольника
Прямоугольник. Квадрат. Периметр многоугольника Естественный отбор. Бинарный урок по биологии и математике (часть 3)
Естественный отбор. Бинарный урок по биологии и математике (часть 3) Понятие обыкновенной дроби. Упражнения
Понятие обыкновенной дроби. Упражнения Урок математики. 1 класс
Урок математики. 1 класс Ответы для самопроверки
Ответы для самопроверки Квадратный корень и его свойства
Квадратный корень и его свойства Математика в кинематографии
Математика в кинематографии Решение задач на готовых чертежах. Геометрия. 9 класс
Решение задач на готовых чертежах. Геометрия. 9 класс Презентация на тему Окружность и круг (5 класс)
Презентация на тему Окружность и круг (5 класс)  Работа над ошибками
Работа над ошибками Алгоритм вычисления площади с помощью палетки
Алгоритм вычисления площади с помощью палетки ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ
ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ Презентация на тему Параллелепипед (9 класс)
Презентация на тему Параллелепипед (9 класс)  Алгоритм фронта волны
Алгоритм фронта волны Числовая последовательность. Арифметическая прогрессия и геометрическая прогрессия
Числовая последовательность. Арифметическая прогрессия и геометрическая прогрессия