Слайд 2Цель
Изучение признаков параллелограмма и трапеции.

Слайд 3Свойства сторон, углов и диагоналей параллелограмма
АВ || CD
BC || AD
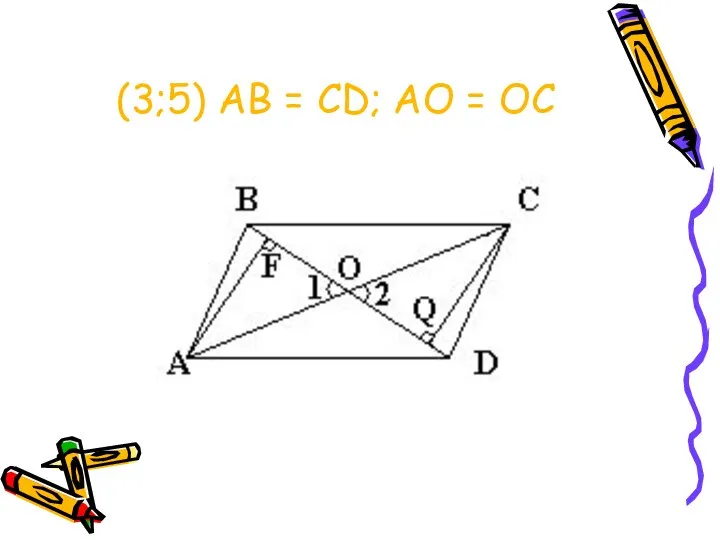
AB = CD
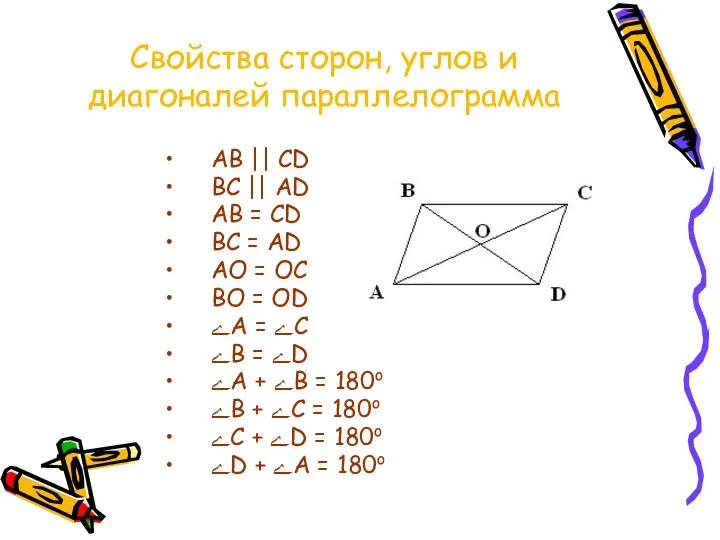
BC = AD
AO = OC
BO = OD
ےA = ےC
ےB = ےD
ےA + ےB = 180o
ےB + ےC = 180o
ےC + ےD = 180o
ےD + ےA = 180o
Слайд 4Группировка свойств параллелограмма
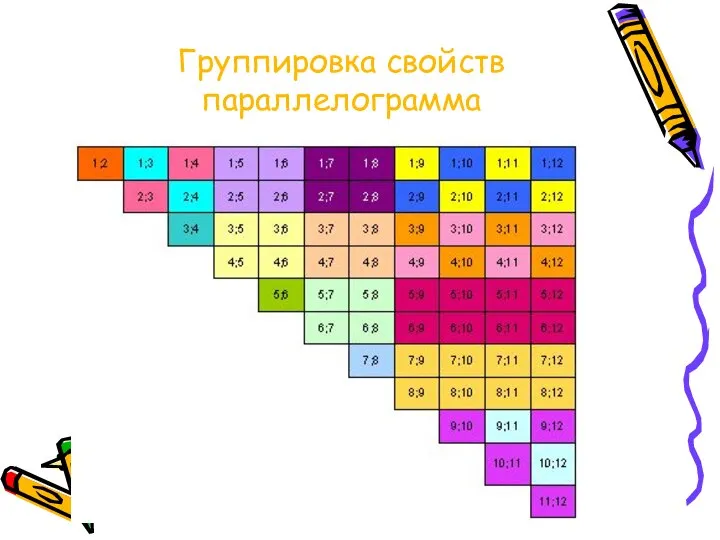
Слайд 6Признаки параллелограмма
Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник

– параллелограмм.
Если в четырёхугольнике две стороны параллельны и диагонали точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.
Если в четырёхугольнике две стороны параллельны и два противоположных угла равны, то этот четырёхугольник – параллелограмм.
Если в четырёхугольнике две стороны параллельны и два смежных угла, принадлежащих одной из сторон, в сумме дают 180o, то этот четырёхугольник – параллелограмм.
Слайд 7Если в четырёхугольнике противоположные стороны соответственно равны, то этот четырёхугольник – параллелограмм.
Если

в четырёхугольнике две стороны равны и диагонали точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.
Если в четырёхугольнике две стороны равны и два смежных угла, принадлежащих одной из сторон, в сумме дают 180o, то этот четырёхугольник – параллелограмм.
Если в четырёхугольнике диагонали точкой пересечения делятся пополам и два смежных угла, принадлежащих одной из сторон, в сумме дают 180o, то этот четырёхугольник – параллелограмм.
Если в четырёхугольнике смежные углы одной стороны и другой, не противоположной, в сумме дают 180o, то этот четырёхугольник – параллелограмм.
Слайд 8Свойства трапеции
ВС || АD
АВ СD
ےA + ےB = 180o
ےC + ےD =
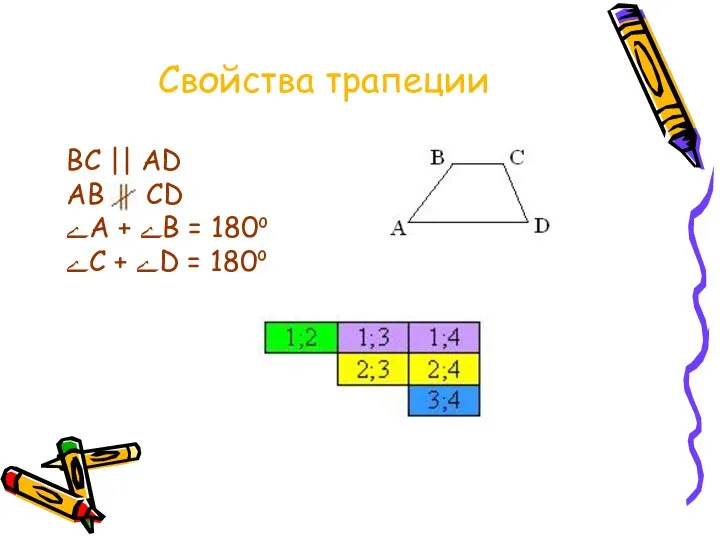
180o
Слайд 9Признак трапеции
Если в четырёхугольнике две стороны не параллельны, сумма двух прилежащих к

одной стороне углов равна 180o, то этот четырёхугольник – трапеция.
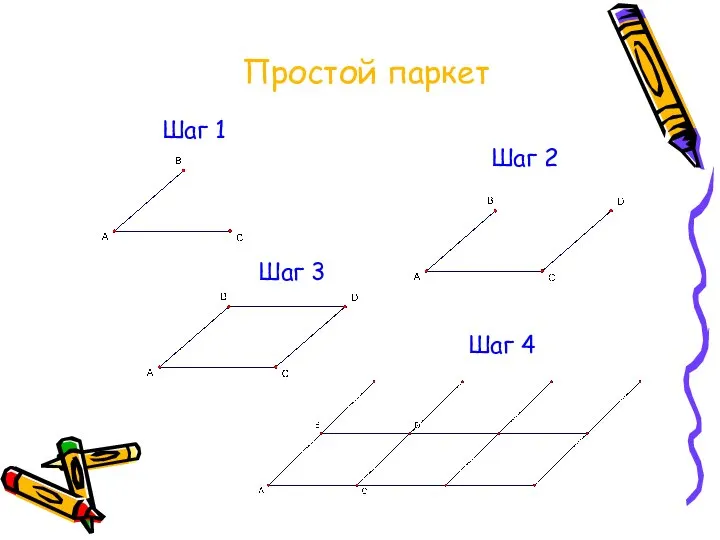
Слайд 13Шаг 1
Шаг 2
Шаг 3
Шаг 4
Простой паркет
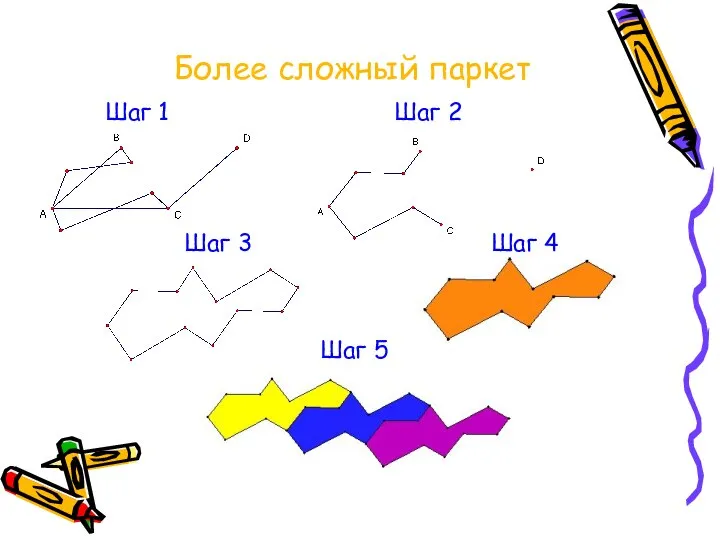
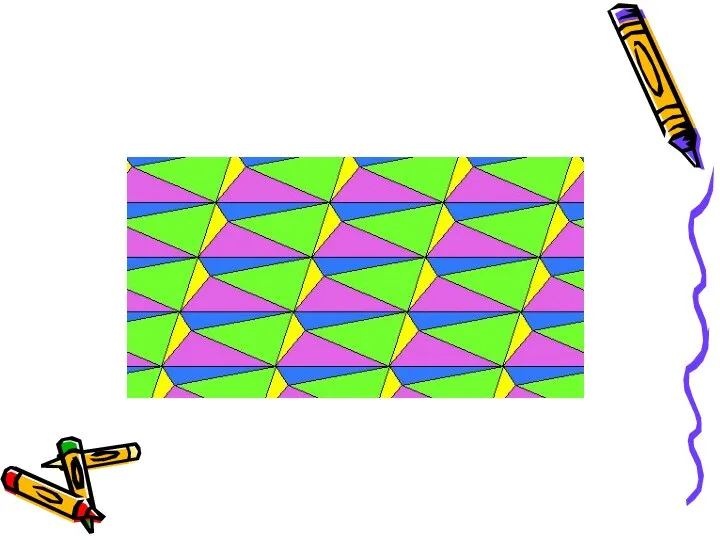
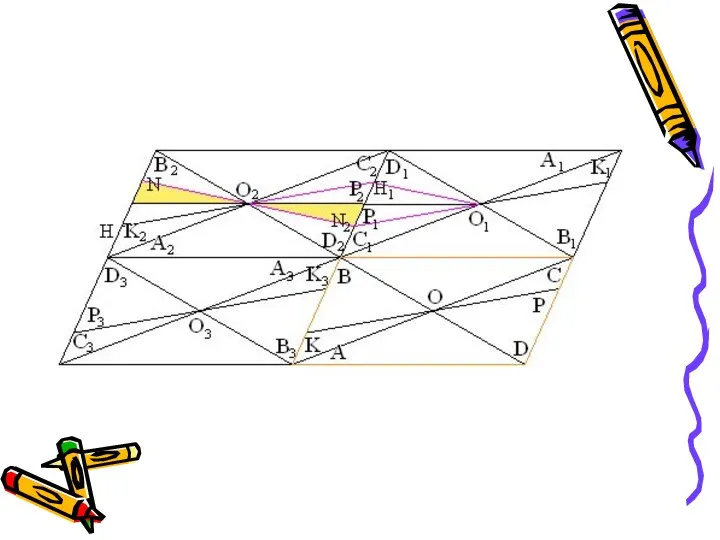
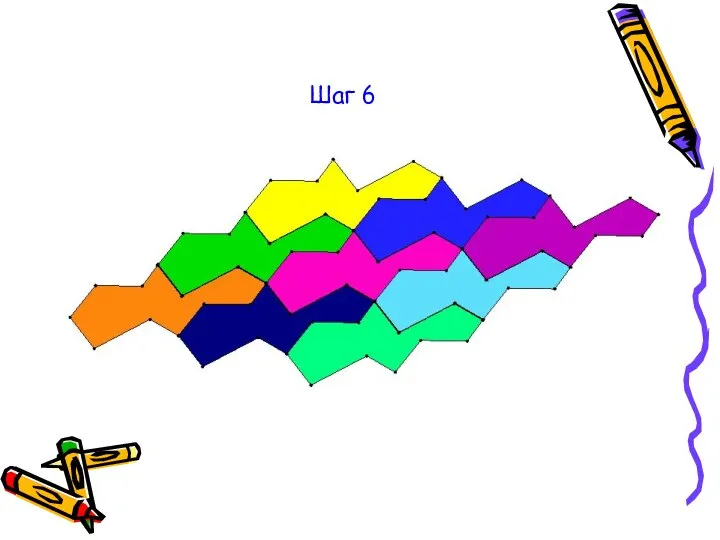
Слайд 14Более сложный паркет
Шаг 1
Шаг 2
Шаг 3
Шаг 4
Шаг 5










 Разность и её значение
Разность и её значение Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Числительные. Количественные числительные
Числительные. Количественные числительные Оценочная и сравнительная классификация алгоритмов
Оценочная и сравнительная классификация алгоритмов Движение в пространстве
Движение в пространстве Эйлеровы графы. Лекция 08
Эйлеровы графы. Лекция 08 Перпендикулярные прямые в пространстве
Перпендикулярные прямые в пространстве Решение квадратных уравнений с параметрами. Метод плавающей параболы
Решение квадратных уравнений с параметрами. Метод плавающей параболы Понятие неравенство
Понятие неравенство Степень с отрицательным показателем
Степень с отрицательным показателем Математическая логика
Математическая логика Презентация на тему Простейшие задачи в координатах (9 класс)
Презентация на тему Простейшие задачи в координатах (9 класс)  Построение 3 видов группы геометрических тел
Построение 3 видов группы геометрических тел Занимательные головоломки
Занимательные головоломки Сложение однозначных чисел с переходом через десяток вида * + 6
Сложение однозначных чисел с переходом через десяток вида * + 6 Правила комбинаторики. Практическое занятие
Правила комбинаторики. Практическое занятие Случаи вычитания 18 -
Случаи вычитания 18 - Сумма углов в треугольнике
Сумма углов в треугольнике Функции у=|x| и ей график
Функции у=|x| и ей график Косвенные измерения
Косвенные измерения Azərbaycan Dövlət Neft və Sənaye Universiteti Optimal Control
Azərbaycan Dövlət Neft və Sənaye Universiteti Optimal Control Решение задач геометрия
Решение задач геометрия Координаты
Координаты Графики функции
Графики функции Раскрытие скобок
Раскрытие скобок Первый признак равенства треугольников
Первый признак равенства треугольников Презентация на тему Прибавление числа 5 (1 класс)
Презентация на тему Прибавление числа 5 (1 класс)  Золотое сечение и симметрия
Золотое сечение и симметрия