Содержание
- 2. * Технологическая карта дистанционного занятия по математике 10 а класс (09.11.2021) Учитель: Чернова Т.В.
- 3. Использование равносильных переходов. Рассматрим решение неравенств, содержащих переменную под знаком квадратного корня. Некоторые методы решения иррациональных
- 4. Использование равносильных переходов. Некоторые методы решения иррациональных неравенств.
- 5. Использование равносильных переходов. Выведем схемы решения трех основных типов иррациональных неравенств используя свойства числовых неравенств и
- 6. Использование равносильных переходов. Следует отметить, что данные переходы справедливы и для нестрогих неравенств. => f(x) ≥0
- 7. Пример №1 Из учебника пример 1 страница 123, записать решение в тетрадь (попробовать решить самостоятельно, а
- 8. Использование равносильных переходов. Условие, при котором неравенство может иметь решения: Тогда: Незначительно отличается переход для нестрогого
- 9. Пример 2. Использование равносильных переходов. функция не имеет нулей при любом х Методы Переходы
- 10. Решение примера 2 из учебника стр 123 (попробовать решить самостоятельно, а затем проверить по учебнику) *
- 11. Использование равносильных переходов. Тогда неравенство выполнено при любом х ϵ ОДЗ Решения у такого неравенства могут
- 12. Пример 3. 1 система Использование равносильных переходов. Методы Переходы
- 13. Пример 3. 2 система Объединение решений Использование равносильных переходов. Методы Переходы
- 14. Решение примера 3 из учебника стр 124 (попробовать решить самостоятельно, а затем проверить по учебнику) *
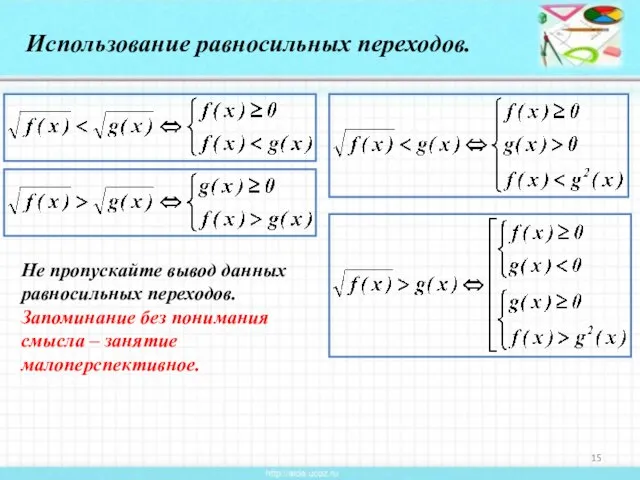
- 15. Использование равносильных переходов. Не пропускайте вывод данных равносильных переходов. Запоминание без понимания смысла – занятие малоперспективное.
- 16. УРОК за 9 ноября закончен!!! Домашнее задание: Прочитать теоремы о равносильности неравенств ( учебник стр. 122-123)
- 17. Учебное занятие на 10 ноября (смотрите технологическую карту на 10 ноября в сетевом городе) *
- 18. Запишите тему: Введение новой переменной.
- 19. Пример 1. Метод введения новой переменной (явная замена). правая и левая части неравенства неотрицательны => имеем
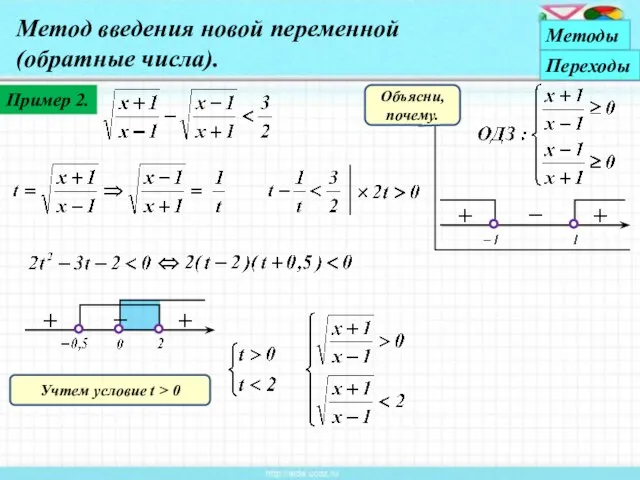
- 20. Пример 2. Метод введения новой переменной (обратные числа). Объясни, почему. Методы Переходы Учтем условие t >
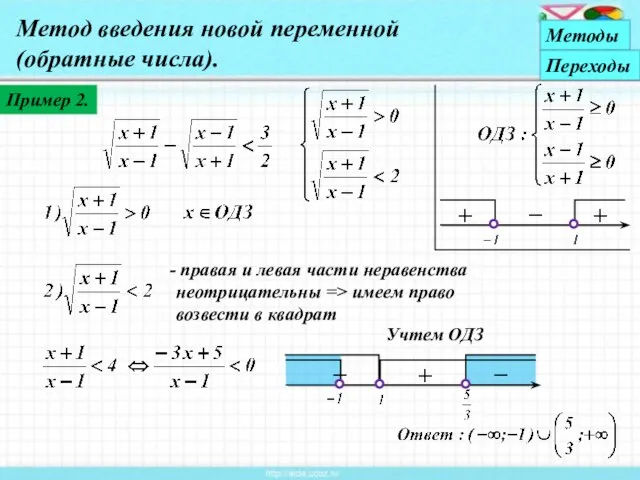
- 21. Пример 2. правая и левая части неравенства неотрицательны => имеем право возвести в квадрат Учтем ОДЗ
- 22. Пример 3. Объясни, почему. Учтем ОДЗ Метод введения новой переменной. Часто, даже если вы не видите
- 24. Скачать презентацию


















 Решение задач по теме Теорема Пифагора
Решение задач по теме Теорема Пифагора Памятка по оформлению краткой записи к задачам
Памятка по оформлению краткой записи к задачам Путь и перемещение
Путь и перемещение Основные сведения о матрицах. Операции над матрицами
Основные сведения о матрицах. Операции над матрицами Элементы нелинейного функционального анализа Глава 1. Дифференциальное исчисление в нормированных пространствах
Элементы нелинейного функционального анализа Глава 1. Дифференциальное исчисление в нормированных пространствах Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3
Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3 Делители числа
Делители числа Золотое сечение
Золотое сечение Найдите производную функции. Практическая работа
Найдите производную функции. Практическая работа Число Пи
Число Пи Движение
Движение Способ группировки
Способ группировки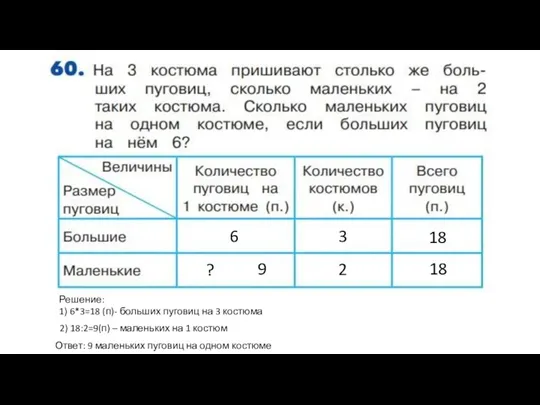 Задача о костюмах
Задача о костюмах Л11 Производная функции
Л11 Производная функции Задачи. Самостоятельная работа
Задачи. Самостоятельная работа Частное целых чисел. 6 класс
Частное целых чисел. 6 класс Исчисление высказываний
Исчисление высказываний Сложение чисел с переходом через десяток в пределах 20
Сложение чисел с переходом через десяток в пределах 20 Функции многих переменных: частные производные, дифференциалы. Лекция 2
Функции многих переменных: частные производные, дифференциалы. Лекция 2 Умножение одночлена на многочлен
Умножение одночлена на многочлен Площади поверхностей и объёмы тел вращения
Площади поверхностей и объёмы тел вращения Октаэдр
Октаэдр В мире цветов и плодов. Интегрированный урок биологии и математики
В мире цветов и плодов. Интегрированный урок биологии и математики Золотой треугольник и много интересного
Золотой треугольник и много интересного Презентация на тему Масштаб и его практическое применение
Презентация на тему Масштаб и его практическое применение  Принак подобия треугольников. Урок 33
Принак подобия треугольников. Урок 33 Симетричні фігури
Симетричні фігури Математические головоломки и игры
Математические головоломки и игры