Параллельность_прямых_в_пространстве_2019

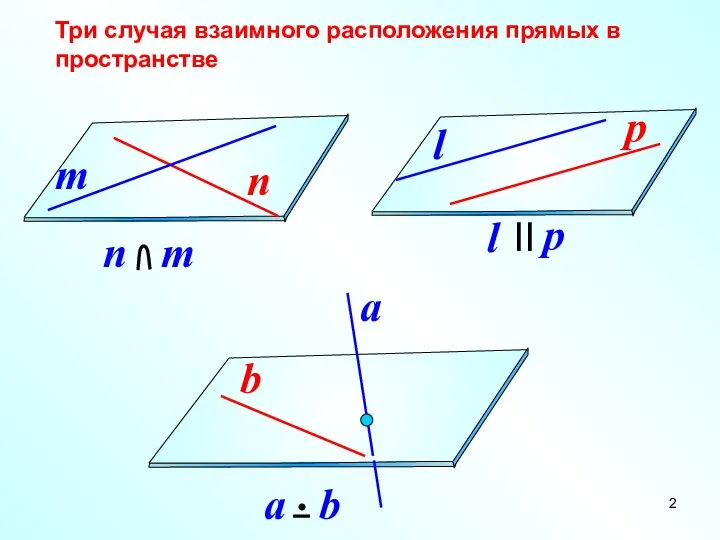
Три случая взаимного расположения прямых в пространстве

Планиметрия
Стереометрия
Две прямые на плоскости называются параллельными, если они не пересекаются.
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
aIIb
aIIb

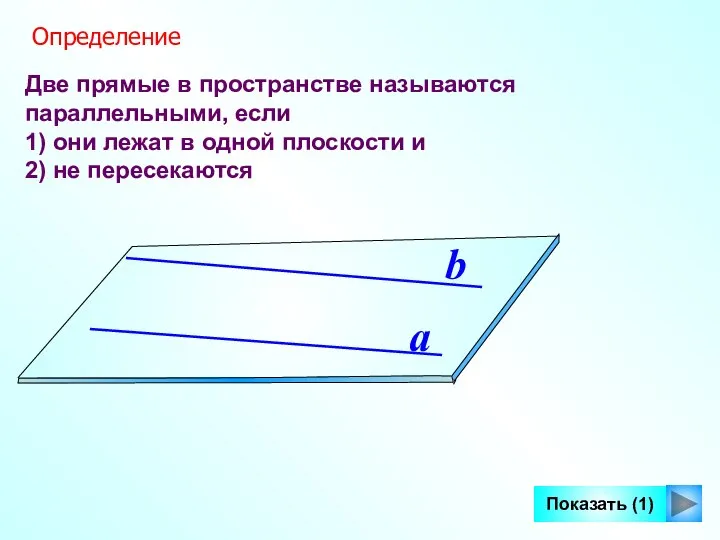
Две прямые в пространстве называются параллельными, если
1) они лежат в одной плоскости и
2) не пересекаются
a
b
Определение
Показать (1)

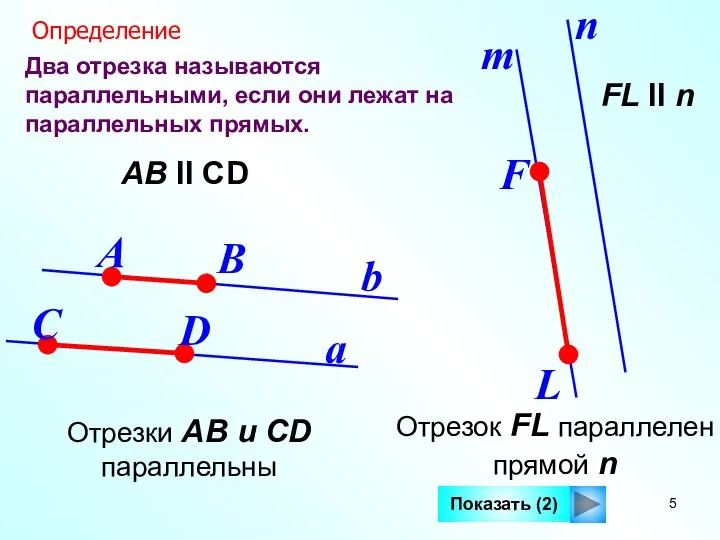
Два отрезка называются параллельными, если они лежат на параллельных прямых.
a
b
Определение
АВ II СD
FL II n
Показать (2)
Отрезок FL параллелен
прямой n
Отрезки АВ и СD параллельны

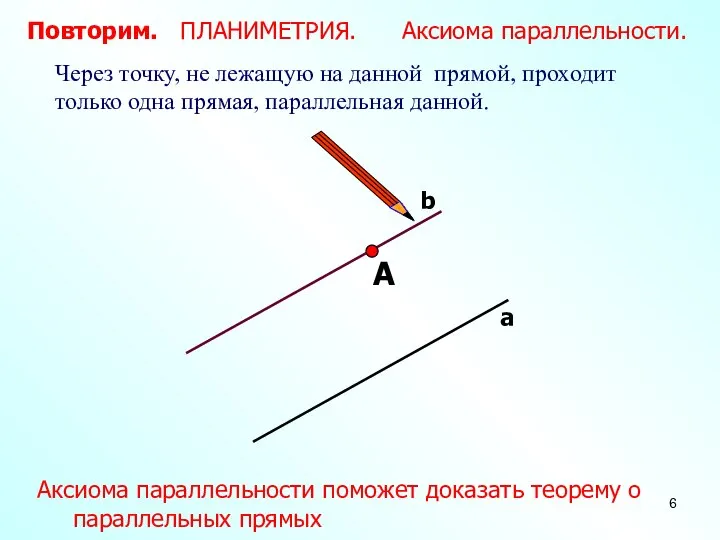
А
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Повторим. ПЛАНИМЕТРИЯ. Аксиома параллельности.
а
b
Аксиома параллельности поможет доказать теорему о параллельных прямых

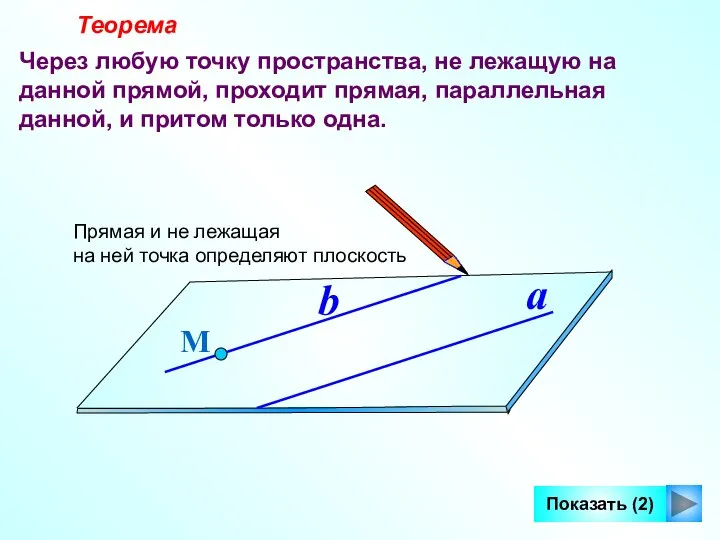
Теорема
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
М
a
b
Прямая и не лежащая
на ней точка определяют плоскость
Показать (2)

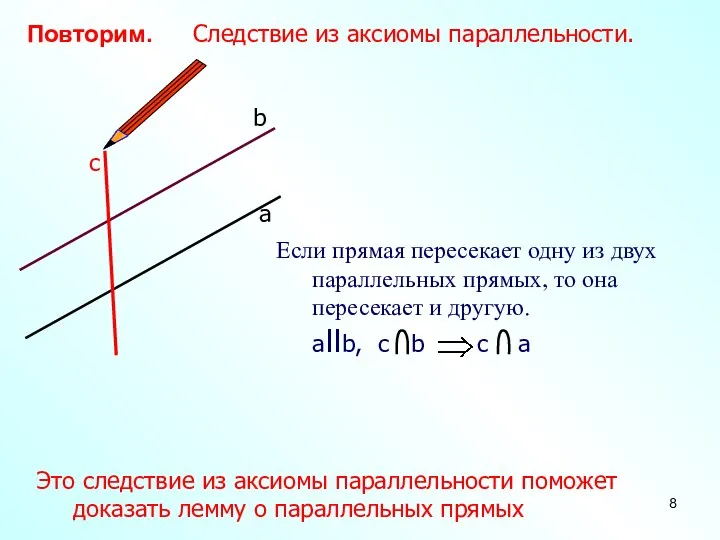
Повторим. Следствие из аксиомы параллельности.
а
c
b
Это следствие из аксиомы параллельности поможет доказать лемму о параллельных прямых

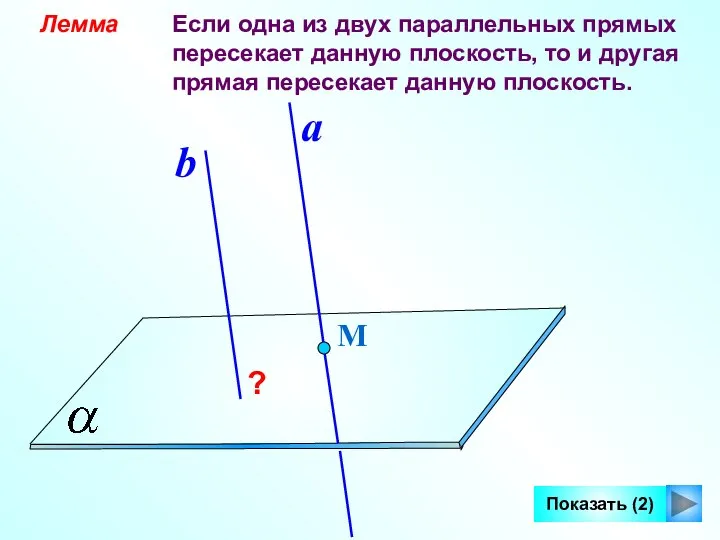
Лемма
Если одна из двух параллельных прямых
пересекает данную плоскость, то и другая
прямая пересекает данную плоскость.
М
Показать (2)
a
?

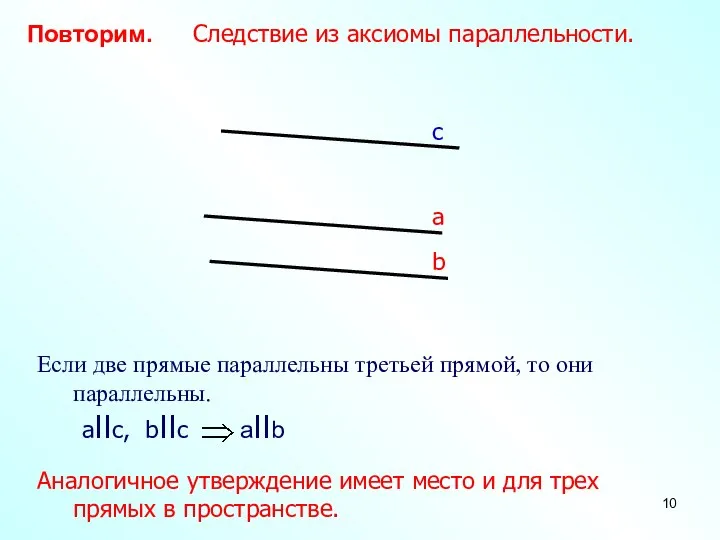
Повторим. Следствие из аксиомы параллельности.
Аналогичное утверждение имеет место и для трех прямых в пространстве.

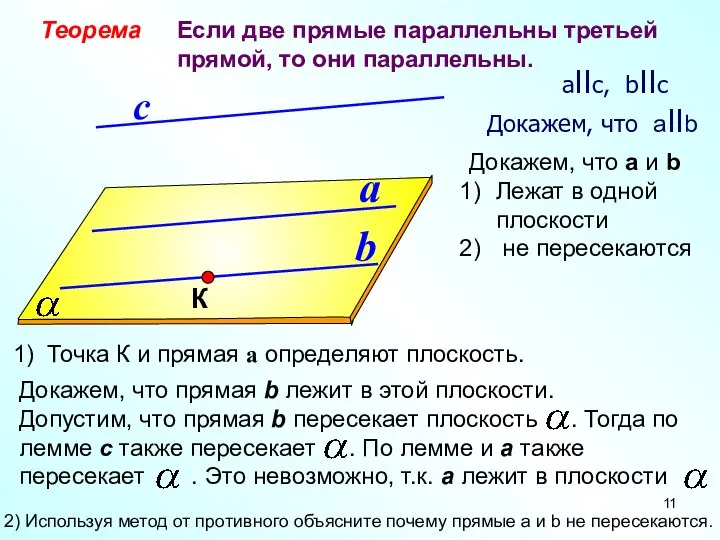
a
b
с
Теорема
Если две прямые параллельны третьей прямой, то они параллельны.
aIIс, bIIс
Докажем, что aIIb
1) Точка К и прямая а определяют плоскость.
Докажем, что а и b
Лежат в одной плоскости
не пересекаются
2) Используя метод от противного объясните почему прямые а и b не пересекаются.

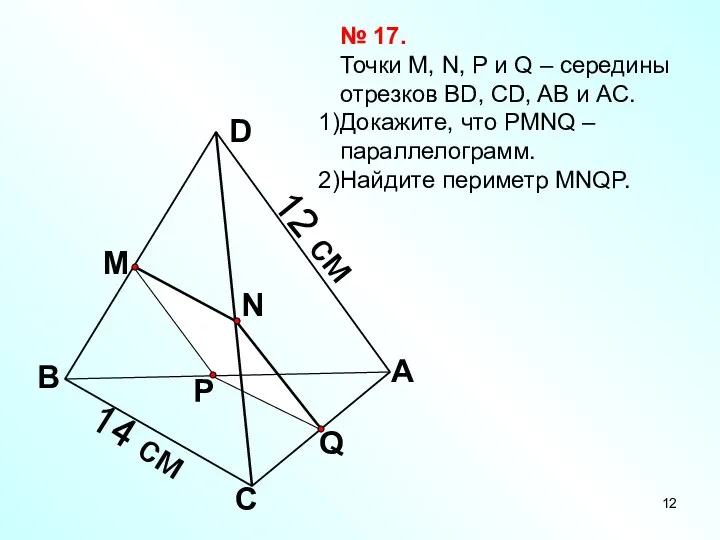
Q
А
С
В
D
N
M
P
№ 17.
Точки М, N, P и Q – середины отрезков BD, CD, AB и АС.
Докажите, что PMNQ – параллелограмм.
Найдите периметр MNQP.
12 см
14 см

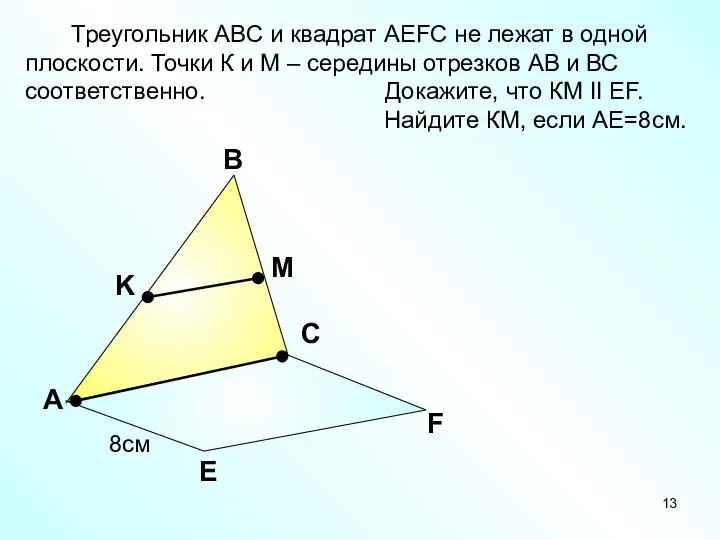
А
В
С
Е
F
K
M
Треугольник АВС и квадрат АEFC не лежат в одной
плоскости. Точки К и М – середины отрезков АВ и ВС соответственно. Докажите, что КМ II EF.
Найдите КМ, если АЕ=8см.
8см

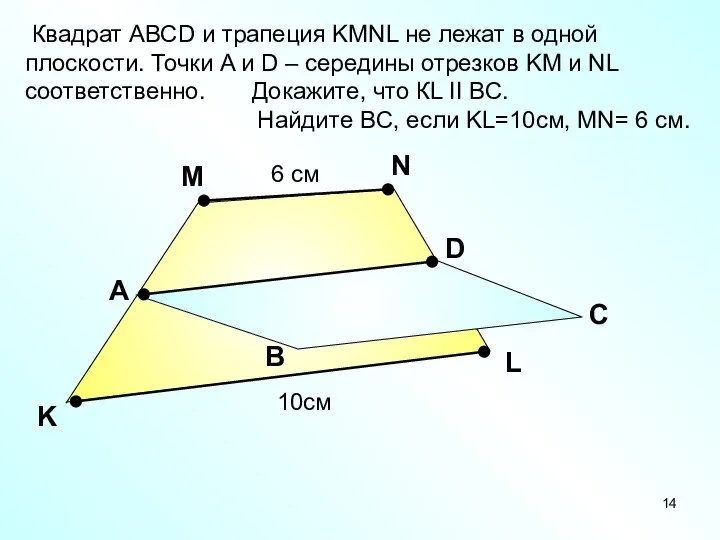
А
В
С
С
D
K
M
Квадрат АВСD и трапеция KMNL не лежат в одной
плоскости. Точки A и D – середины отрезков KM и NL соответственно. Докажите, что КL II BC.
Найдите BC, если KL=10см, MN= 6 см.
N
L
10см
6 см