Содержание
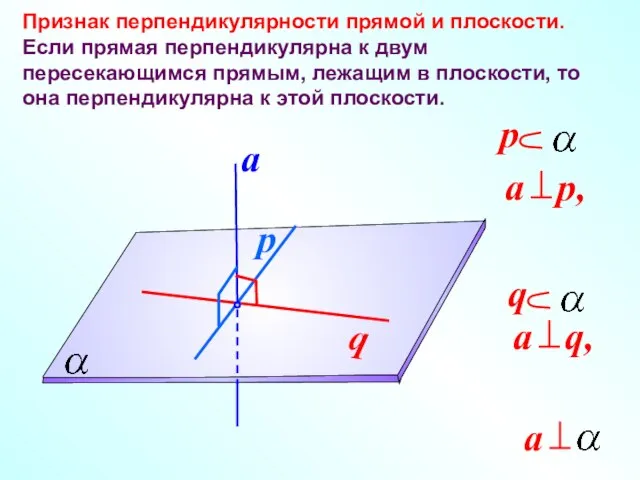
- 2. Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то
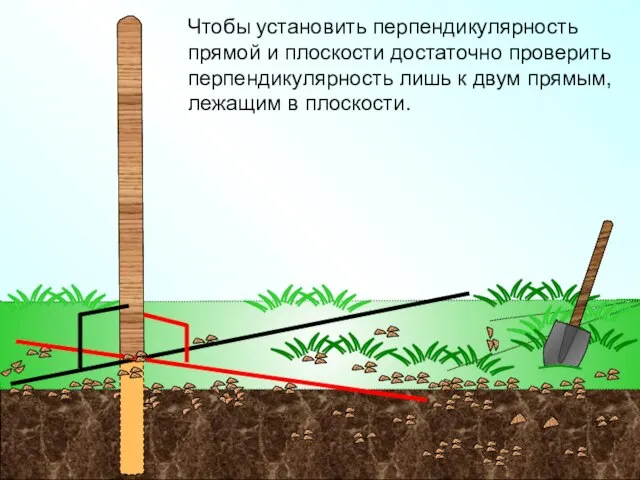
- 3. Чтобы установить перпендикулярность прямой и плоскости достаточно проверить перпендикулярность лишь к двум прямым, лежащим в плоскости.
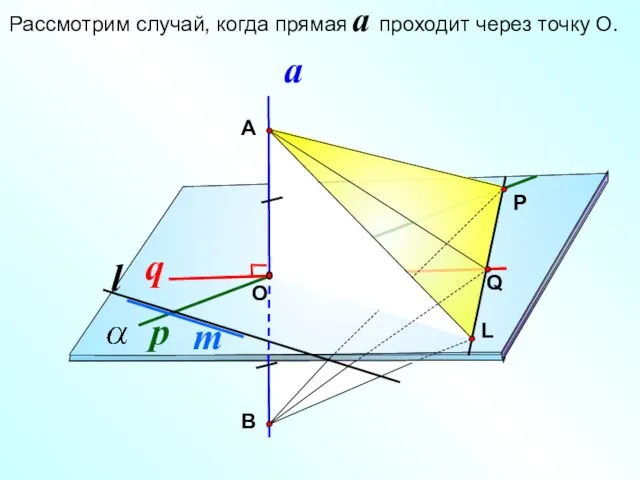
- 5. О Рассмотрим случай, когда прямая a проходит через точку О.
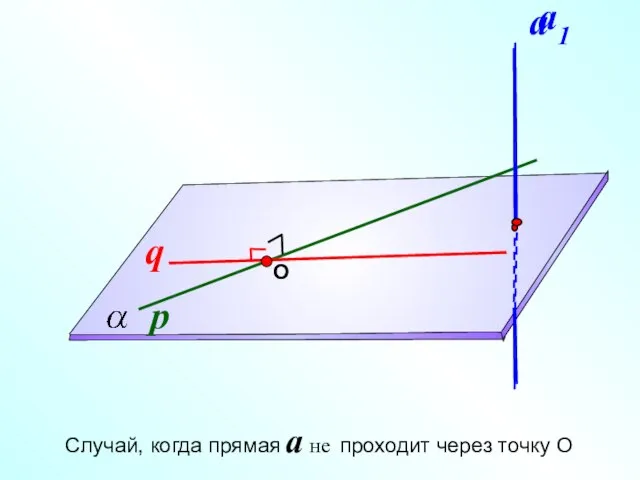
- 6. О Случай, когда прямая a не проходит через точку О
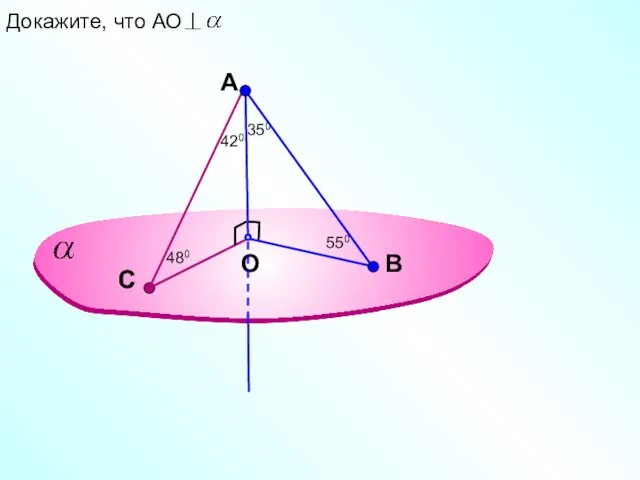
- 7. A O В Докажите, что АО С С 350 550 420 480
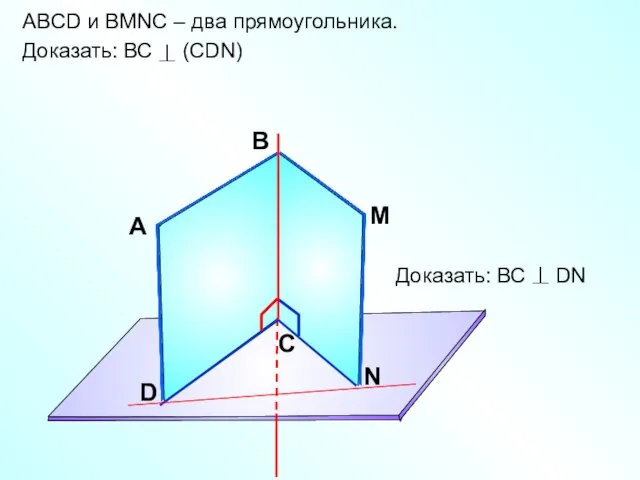
- 8. ABCD и ВMNС – два прямоугольника. Доказать: ВС (СDN) А В С D M N
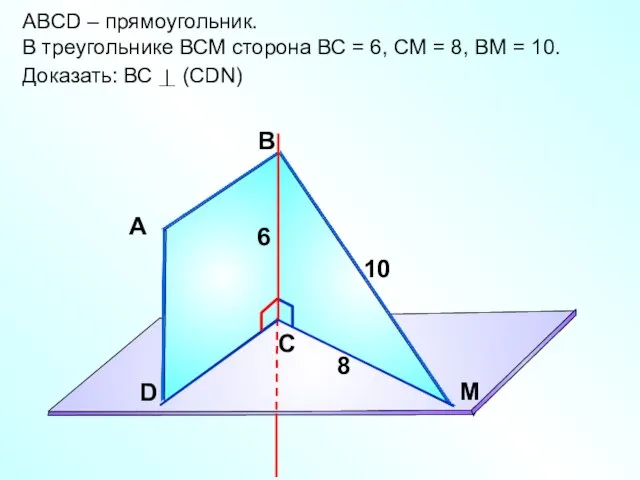
- 9. ABCD – прямоугольник. В треугольнике ВСМ сторона ВС = 6, СМ = 8, ВМ = 10.
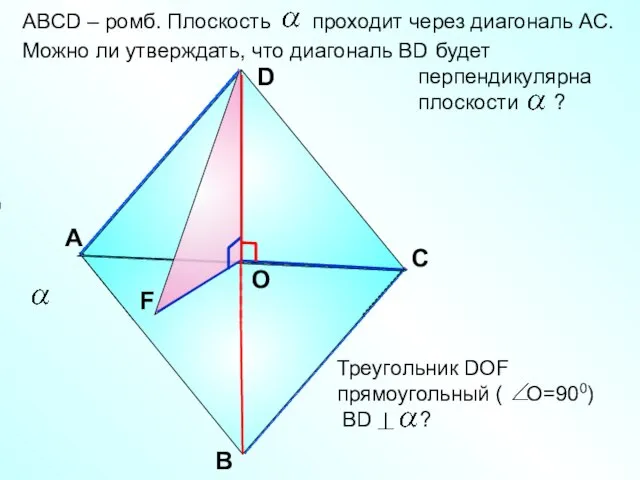
- 10. ABCD – ромб. Плоскость проходит через диагональ АС. Можно ли утверждать, что диагональ ВD будет перпендикулярна
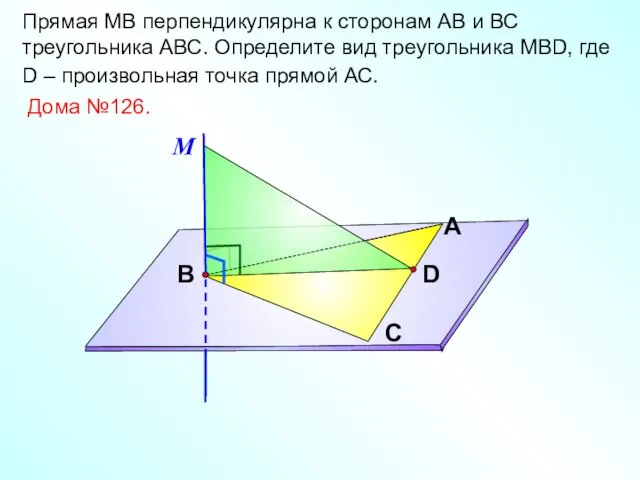
- 11. Прямая МВ перпендикулярна к сторонам АВ и ВС треугольника АВС. Определите вид треугольника МВD, где D
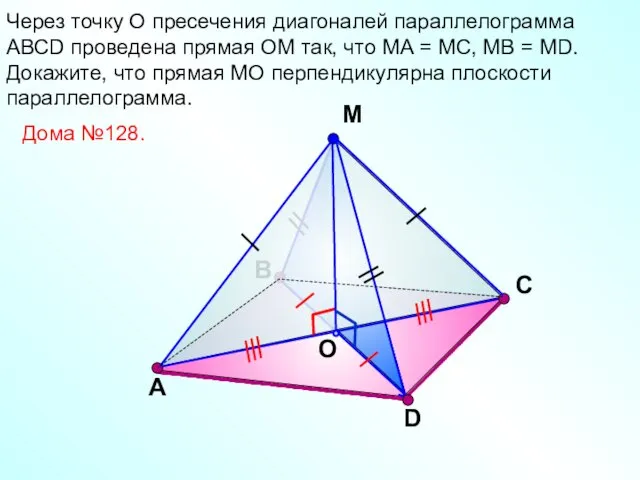
- 12. В М O С Через точку О пресечения диагоналей параллелограмма АВСD проведена прямая ОМ так, что
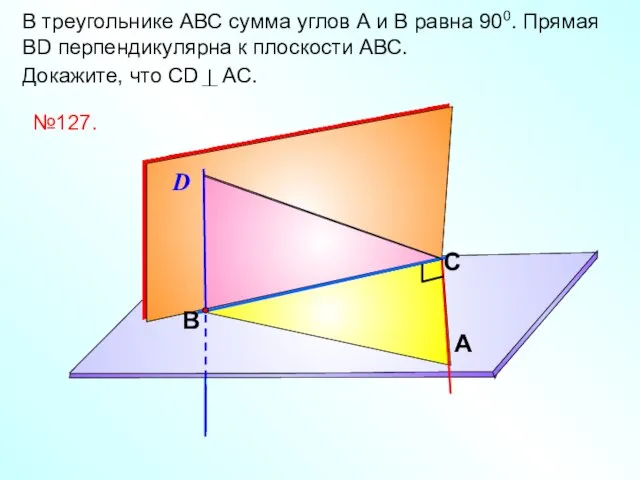
- 13. В треугольнике АВС сумма углов А и В равна 900. Прямая ВD перпендикулярна к плоскости АВС.
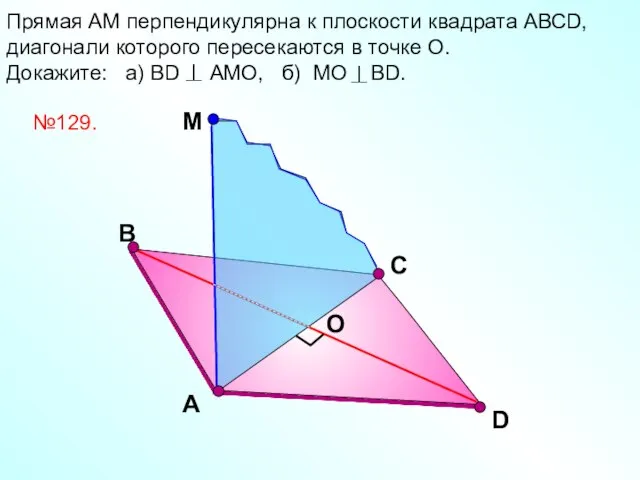
- 14. D Прямая АМ перпендикулярна к плоскости квадрата АВСD, диагонали которого пересекаются в точке О. Докажите: а)
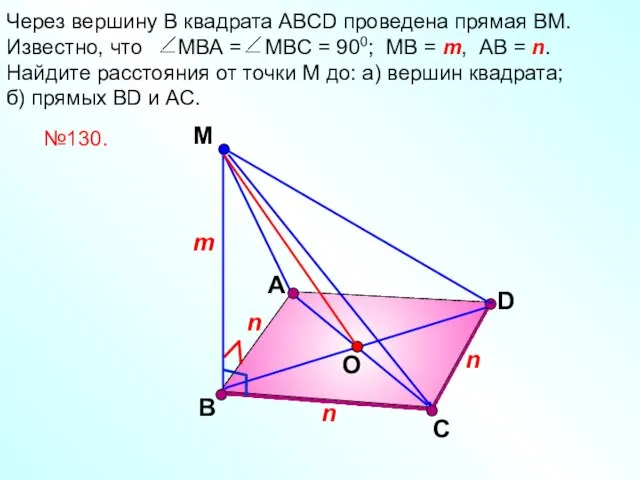
- 15. А М D Через вершину В квадрата АВСD проведена прямая ВМ. Известно, что МВА = МВС
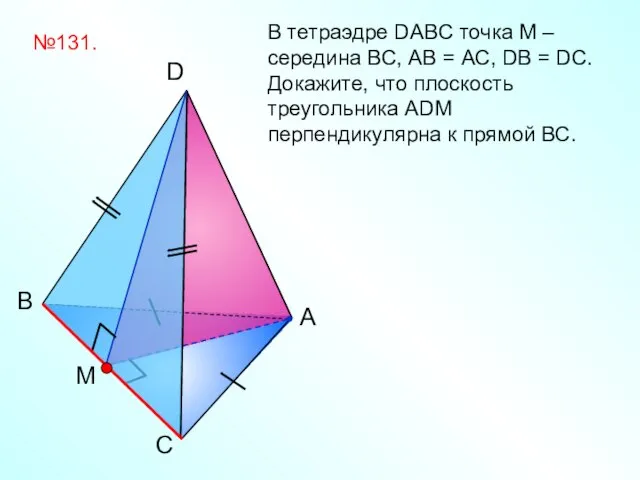
- 16. С B A D В тетраэдре DABC точка М – середина BС, АB = АС, DВ
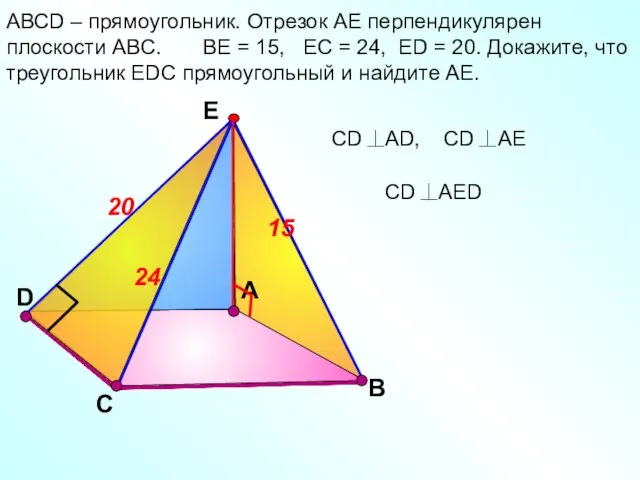
- 17. D А АВСD – прямоугольник. Отрезок АЕ перпендикулярен плоскости АВС. ВЕ = 15, ЕС = 24,
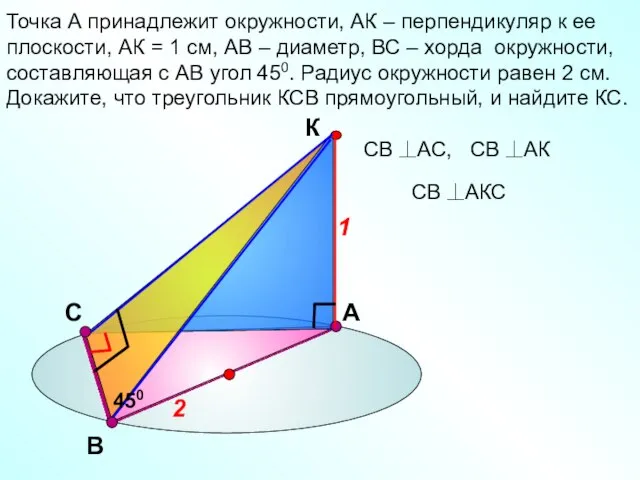
- 18. С Точка А принадлежит окружности, АК – перпендикуляр к ее плоскости, АК = 1 см, АВ
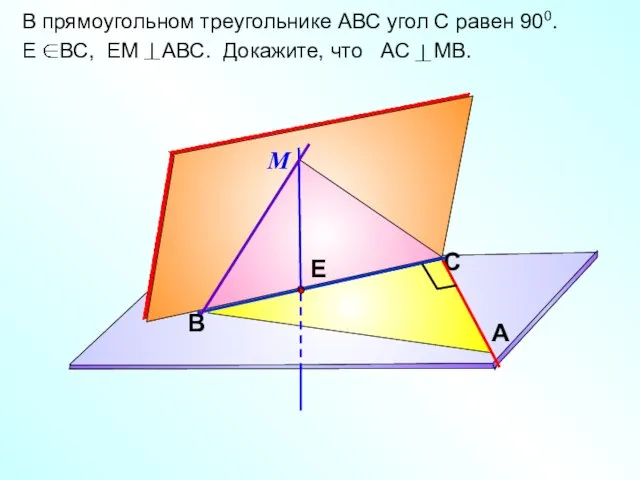
- 19. В прямоугольном треугольнике АВС угол С равен 900. Е ВС, ЕМ АВС. Докажите, что АС МВ.
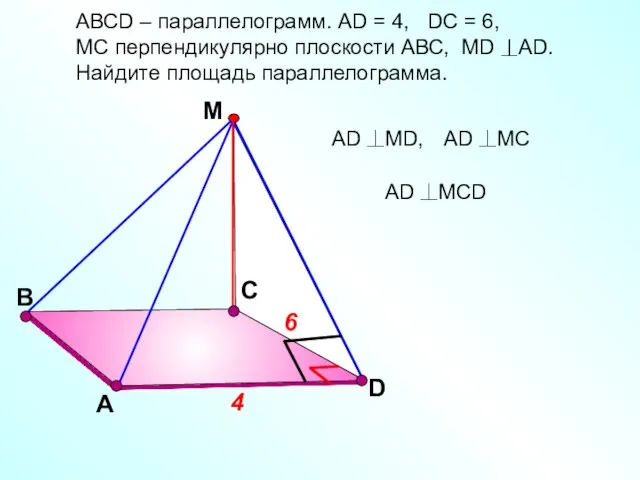
- 20. В С А М 6 4 D
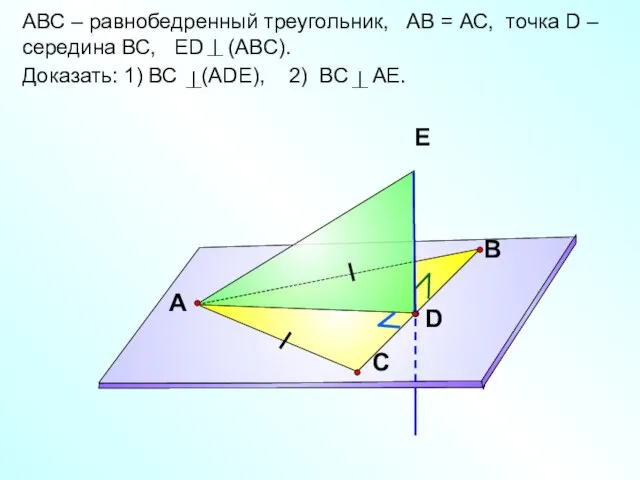
- 21. АВС – равнобедренный треугольник, АВ = АС, точка D – середина ВС, ЕD (ABC). Доказать: 1)
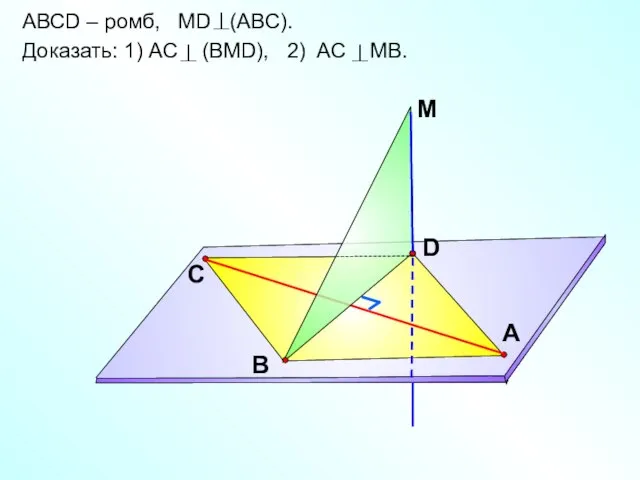
- 22. АВСD – ромб, МD (ABC). Доказать: 1) AС (BMD), 2) AС MB. D С А B
- 24. Скачать презентацию

 Многогранники
Многогранники Интервальные оценки
Интервальные оценки Презентация на тему Квадратный дециметр (3 класс)
Презентация на тему Квадратный дециметр (3 класс)  Формальные логические теории
Формальные логические теории Методика изучения времени. Время
Методика изучения времени. Время Презентация на тему Функция у=х^3 и её график
Презентация на тему Функция у=х^3 и её график  Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Презентация на тему Элементы статистики
Презентация на тему Элементы статистики  Путешествие по стране высшей математики
Путешествие по стране высшей математики Признаки параллельности прямых
Признаки параллельности прямых Презентация по математике "Использование информационных технологий в преподавании математики" -
Презентация по математике "Использование информационных технологий в преподавании математики" -  Математика. Прогулка в осенний лес. 2 класс
Математика. Прогулка в осенний лес. 2 класс Итоговое повторение. Алгебра. 8 класс
Итоговое повторение. Алгебра. 8 класс Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Площадь фигур. Решение задач
Площадь фигур. Решение задач Вторая производная функции и ее физической смысл
Вторая производная функции и ее физической смысл Окружности. Центр окружности
Окружности. Центр окружности Число 10
Число 10 Формулы сокращённого умножения
Формулы сокращённого умножения Гипотенуза и катеты в треугольнике. Задачи
Гипотенуза и катеты в треугольнике. Задачи Лекция 0
Лекция 0 Вычисление вероятностей событий с использованием формулы полной вероятности и формулы Байеса
Вычисление вероятностей событий с использованием формулы полной вероятности и формулы Байеса Сантиметр - единица измерения длины
Сантиметр - единица измерения длины Уравнение cosx = a
Уравнение cosx = a Площадь фигур. Решение задач по готовым чертежам
Площадь фигур. Решение задач по готовым чертежам Векторная алгебра. Векторы на плоскости и в трехмерном пространстве, линейные операции над ними
Векторная алгебра. Векторы на плоскости и в трехмерном пространстве, линейные операции над ними Вычитание вида 13
Вычитание вида 13 Урок алгебры в 8 классе
Урок алгебры в 8 классе