Содержание
- 2. Джон Непер - изобретатель системы логарифмов, основанной на установ- лении соответствия между арифмети- ческой и геометрической
- 3. Основное логарифмическое тождество
- 4. Логарифмом положительного числа b по основанию а, где а>0, а≠1, называется показатель степени, в которую надо
- 5. Определение логарифма Из определения логарифма следует, что нахождение x = logab равносильно решению уравнения ax =
- 6. 4log45 = Используя основное логарифмическое тождество, найдите значения выражения 5 3log317 = 17 132log1316 = 256
- 7. Логарифмирование Логарифмированием называют действие нахождения логарифма числа. Читается: логарифм b по основанию a. log525=2, log4(1/16)=-2, log1/327
- 8. Найдите значения выражения log5626= log327= log0,54= log100,001= log111= log381= 4 3 -3 -2 0 4
- 9. Логарифмирование Найти логарифмы чисел b по основанию а Ответ: 2,25 Ответ: 1,5 Ответ: -5
- 10. Логарифмирование Найти x По определению логарифма Так как Откуда то
- 11. При каких значениях х существует логарифм Не существует
- 12. Доказательство основных свойств логарифмов
- 13. Логарифм произведения положительных чисел равен сумме логарифмов множителей Логарифм произведения Пусть а>0, a=1, c>0. Тогда Докажем
- 14. Логарифм произведения Известно: Перемножим почленно равенства (2) и (3) (2) (3) Формула (1) доказана
- 15. Логарифм произведения
- 16. Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя Логарифм частного Пусть а>0, a=1,
- 17. Логарифм частного Известно: Разделим почленно равенства (2) и (3) (2) (3) Формула (1) доказана
- 18. Логарифм частного
- 19. Логарифм степени с положительным основанием равен показателю степени, умноженному на логарифм основания степени Логарифм степени Пусть
- 20. Логарифм степени Возводя основание логарифмического тождества в степень r получаем: откуда по определению логарифма следует формула
- 21. Логарифм степени
- 22. Переход к новому основанию Для перехода от логарифма по одному основанию к логарифму по другому основанию
- 23. Переход к новому основанию Запишем основное логарифмическое тождество Возьмем от обеих его частей логарифмы по основанию
- 24. Переход к новому основанию Следствие. При b=c –происходит перестановка основания и логарифмируемого выражения
- 25. Переход к новому основанию
- 26. Свойства логарифмов
- 27. 1) 3log317 = 17; 132log1316 = 256 (13log1316)2= =162 = Примеры: a>0, a≠1, b>0
- 28. 2) 1 Пример: 1 3) 0 Пример: 0 a>0, a≠1 a>0, a≠1
- 29. 4) Пример: 5) Пример: a>0, a≠1, b>0 a>0, a≠1, b>0, r-любое действительное число
- 30. 6) Пример: a>0, a≠1, b>0, r - любое действительное число
- 31. 7) Пример: a>0, a≠1, b>0,c>0
- 32. 8) Пример: a>0, a≠1, b>0,c>0
- 33. 9) Пример: a>0, a≠1, b>0,c ≠1
- 34. 10) Пример: a>0, a≠1, b>0, b ≠1
- 35. 11) Пример: a>0, a≠1, c>0
- 36. 12) Пример: a>0, a≠1, b>0
- 38. Скачать презентацию

























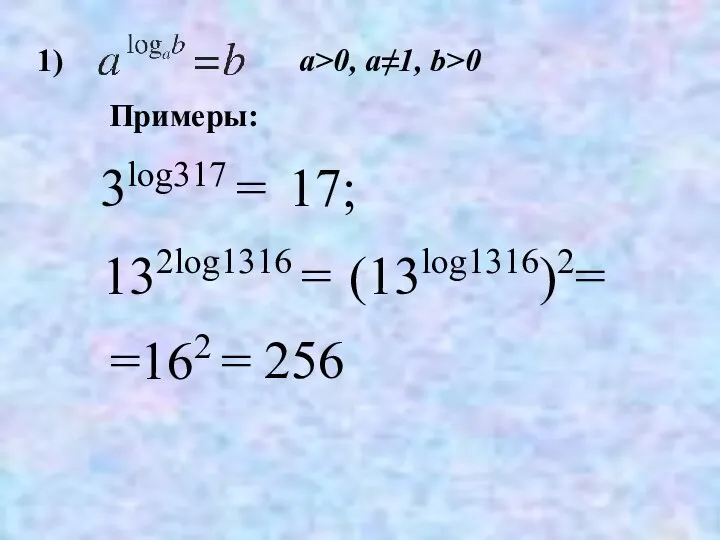
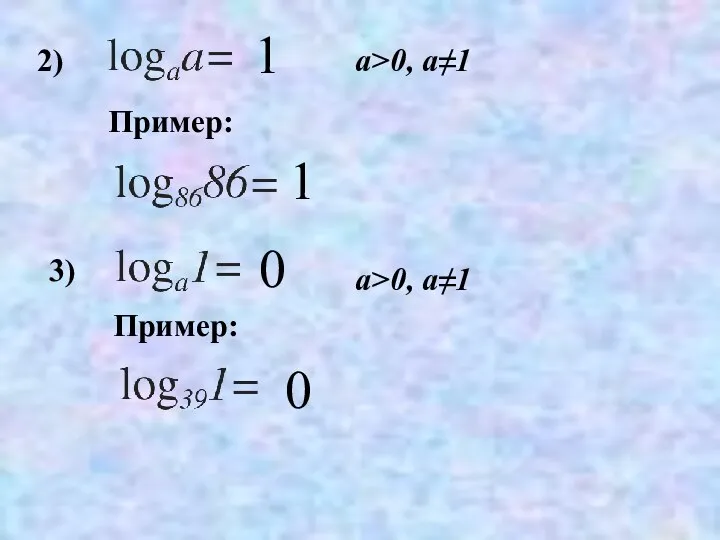

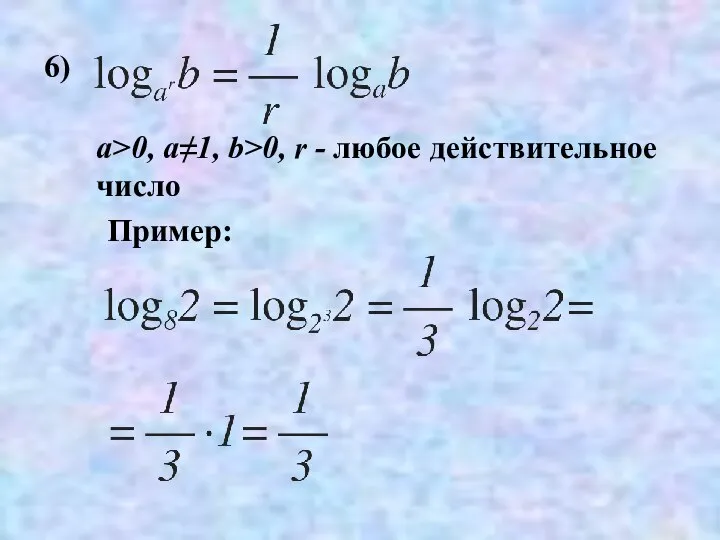
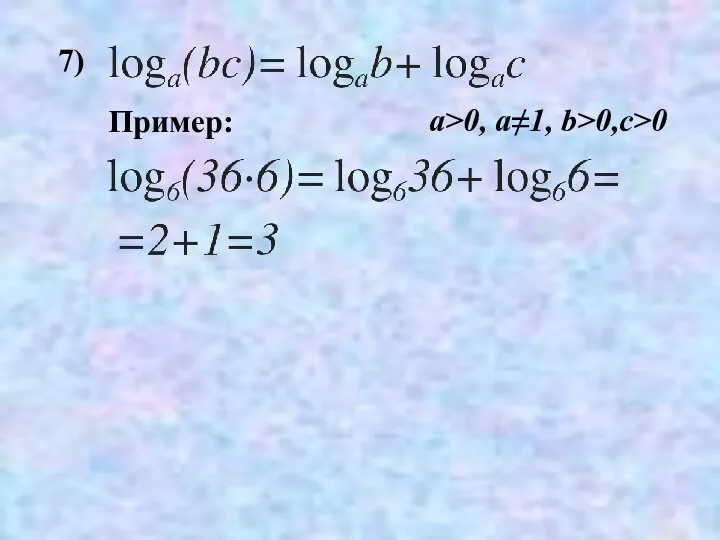
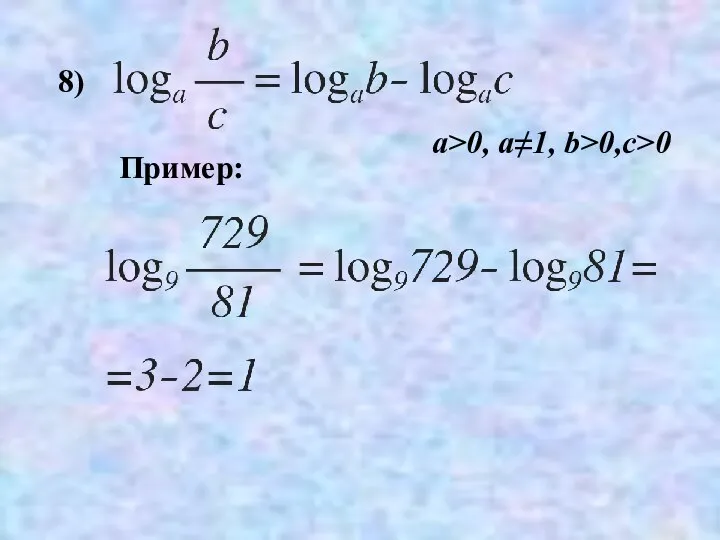
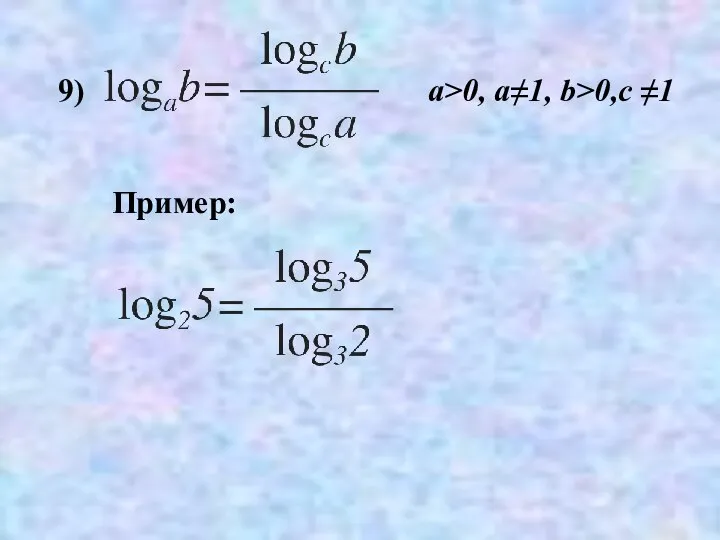
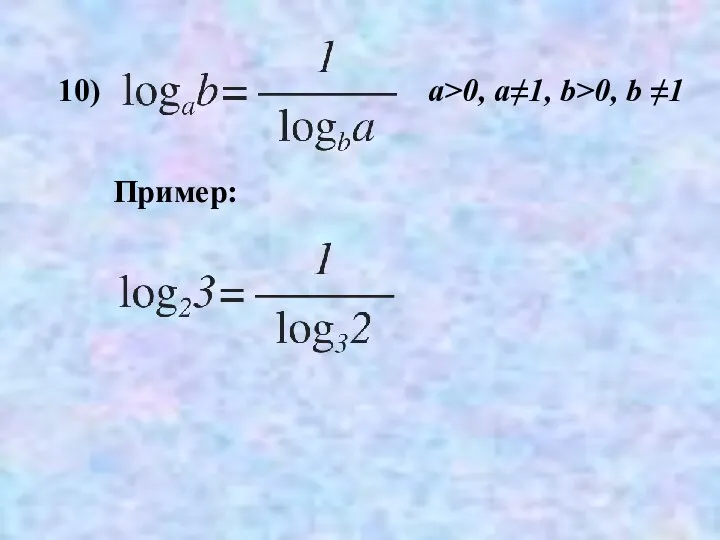
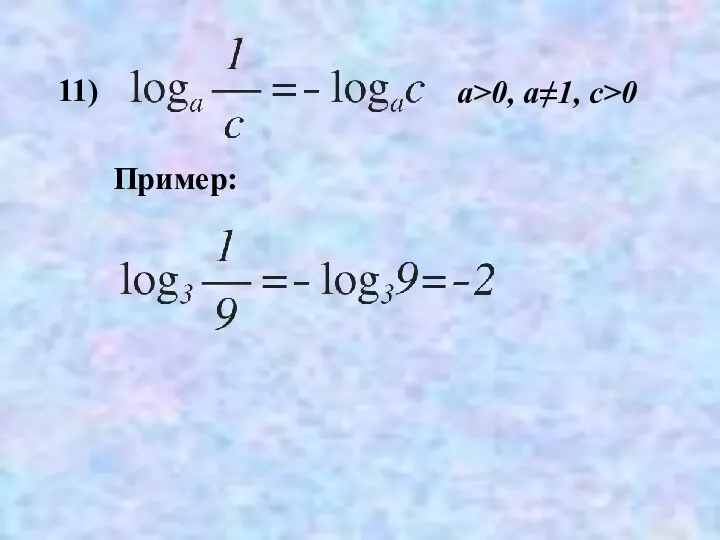
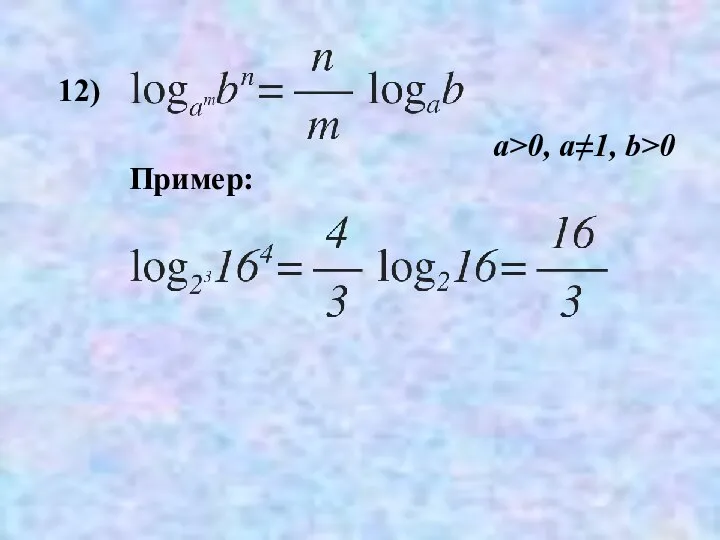
 Сложение векторов
Сложение векторов Среднее арифметическое. 5 класс
Среднее арифметическое. 5 класс Презентация на тему Решение уравнений графическим способом
Презентация на тему Решение уравнений графическим способом  Начальные понятия геометрии
Начальные понятия геометрии Алгебра. Число. Уравнение. Тождество. Функция
Алгебра. Число. Уравнение. Тождество. Функция Неравенства и их системы
Неравенства и их системы Решение тригонометрических уравнений
Решение тригонометрических уравнений Многоугольники (n-угольники)
Многоугольники (n-угольники) Интегрированный урок: Многогранники вокруг нас
Интегрированный урок: Многогранники вокруг нас Формулы площади
Формулы площади Презентация на тему Описательная статистика
Презентация на тему Описательная статистика  Робот Гоша ведёт занятие по ФЭМП
Робот Гоша ведёт занятие по ФЭМП Системы случайных величин
Системы случайных величин Векторы в пространстве. Понятие вектора
Векторы в пространстве. Понятие вектора Презентация на тему Метод координат в пространстве
Презентация на тему Метод координат в пространстве  Задания по математике (5 класс, часть 6)
Задания по математике (5 класс, часть 6) Производная функции. Тест 1
Производная функции. Тест 1 Равенство геометрических фигур
Равенство геометрических фигур Theorem of rational root with integral coefficients
Theorem of rational root with integral coefficients Презентация на тему Задачи на увеличение и уменьшение числа (1 класс)
Презентация на тему Задачи на увеличение и уменьшение числа (1 класс)  Состав числа 10
Состав числа 10 Симметрия в пространстве
Симметрия в пространстве Про Федота стрельца, аглицкого посла и геометрию! Сказка в 4-х действиях
Про Федота стрельца, аглицкого посла и геометрию! Сказка в 4-х действиях Математика и физика здоровья
Математика и физика здоровья Школа олимпийского резерва. (задача)
Школа олимпийского резерва. (задача) Презентация на тему ЛОГАРИФМ ЧИСЛА
Презентация на тему ЛОГАРИФМ ЧИСЛА  Синтез автоматов без памяти
Синтез автоматов без памяти Формирование элементарных математических представлений
Формирование элементарных математических представлений