Содержание
- 2. Выполните задание Для каждой функции определите производную и первообразную 0 ошибок – оценка «5»; 1 ошибка
- 3. Проверим ответы 1-д-ж 2-в-г 3-е-а 4-ж-в 5-а-б 6-г-е 7-б-д
- 4. Вопросы для повторения Что значит решить уравнение? Каков алгоритм решения уравнений? Какие виды уравнений вы умеете
- 5. Тема: «Дифференциальные уравнения первого порядка. Дифференциальные уравнения с разделяющимися переменными»
- 6. Определение дифференциального уравнения Дифференциальное уравнение – это уравнение, в которое наряду с неизвестной функцией входит и
- 7. Автономное уравнение Вид уравнения: Умножим обе части уравнения на dx, Метод решения: Таким образом, проинтегрируем обе
- 8. Уравнение с разделяющимися переменными Вид уравнения: Метод решения: Это уравнение сводится к системе В первом уравнении
- 9. Однородное уравнение Вид уравнения: Линейное однородное уравнение Вид уравнения: Линейное уравнение Вид уравнения: .
- 10. Пример 1. Найдите общее решение дифференциального уравнения
- 11. Пример 2. Найдите общее решение дифференциального уравнения
- 13. Скачать презентацию










 Формирование знаковой культуры на уроках
Формирование знаковой культуры на уроках Математический квест (8 класс)
Математический квест (8 класс) Задачи на нахождение площади прямоугольника и трапеции
Задачи на нахождение площади прямоугольника и трапеции Задачи. 4 класс
Задачи. 4 класс Памятка по оформлению краткой записи к задачам (1 класс)
Памятка по оформлению краткой записи к задачам (1 класс)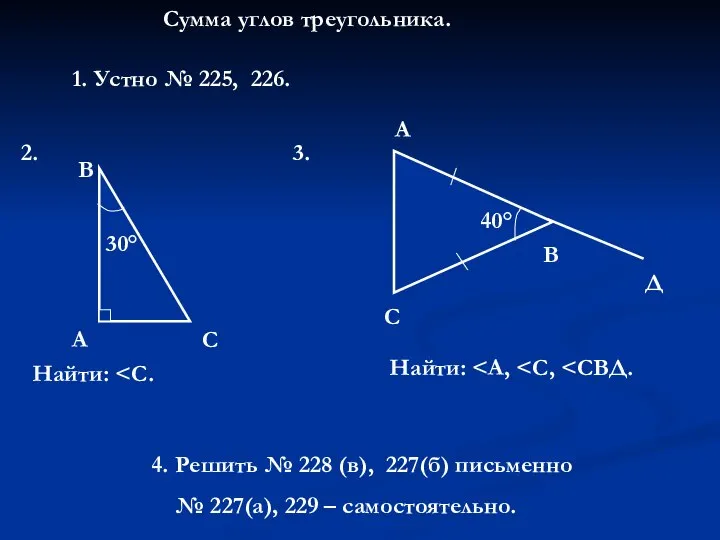 Сумма углов треугольника
Сумма углов треугольника Презентация на тему Буквенные выражения (2 класс)
Презентация на тему Буквенные выражения (2 класс)  Презентация на тему Дробные выражения (6 класс)
Презентация на тему Дробные выражения (6 класс)  ЕГЭ. Экономические задачи IV
ЕГЭ. Экономические задачи IV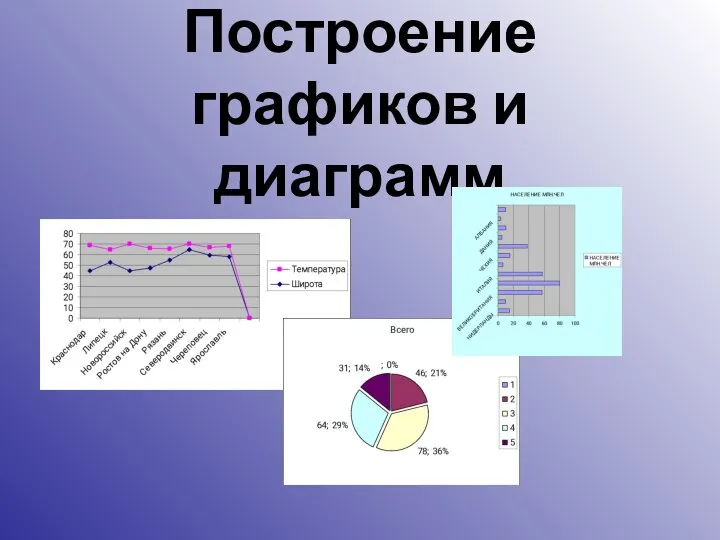 Электронные таблицы. Построение графиков и диаграмм
Электронные таблицы. Построение графиков и диаграмм тригонометрические неравенства
тригонометрические неравенства Случайные величины
Случайные величины Элементы математической логики
Элементы математической логики Числа 1 – 10. Сложение и вычитание
Числа 1 – 10. Сложение и вычитание Решение тригонометрических уравнений приводимых к алгебраическим
Решение тригонометрических уравнений приводимых к алгебраическим Касательная к окружности. 8 класс
Касательная к окружности. 8 класс Линейная алгебра. Система линейных однородных уравнений. Фундаментальная система решений
Линейная алгебра. Система линейных однородных уравнений. Фундаментальная система решений Урок математики в 1 классе
Урок математики в 1 классе Основы стереометрии. Прямая и плоскость. Построение сечений. Угол между прямыми
Основы стереометрии. Прямая и плоскость. Построение сечений. Угол между прямыми Примеры. Карточки, счет +-10, 11, 12
Примеры. Карточки, счет +-10, 11, 12 Многочлен и его стандартный вид
Многочлен и его стандартный вид Обобщение пропорции и лекарственные растения Сибири
Обобщение пропорции и лекарственные растения Сибири Презентация на тему Сложение и вычитание натуральных чисел (5 класс)
Презентация на тему Сложение и вычитание натуральных чисел (5 класс)  Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Периметр многоугольника
Периметр многоугольника Кут. Вимірювання кутів. Рівність кутів. Бісектриса кута
Кут. Вимірювання кутів. Рівність кутів. Бісектриса кута Презентация на тему ИСТОРИЯ ВОЗНИКНОВЕНИЯ ЧАСОВ
Презентация на тему ИСТОРИЯ ВОЗНИКНОВЕНИЯ ЧАСОВ  Раскрытие скобок
Раскрытие скобок