Содержание
- 2. Перпендикулярные прямые в пространстве Две прямые в пространстве называются перпендикулярными (взаимно перпендикуляр-ными), если угол между ними
- 3. Перпендикулярные прямые в пространстве Теорема. Если две пересекающиеся прямые в пространстве параллельны соответственно двум перпендикулярным прямым,
- 4. Перпендикулярность прямой и плоскости Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей
- 5. Свойства : 1. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна другой прямой.
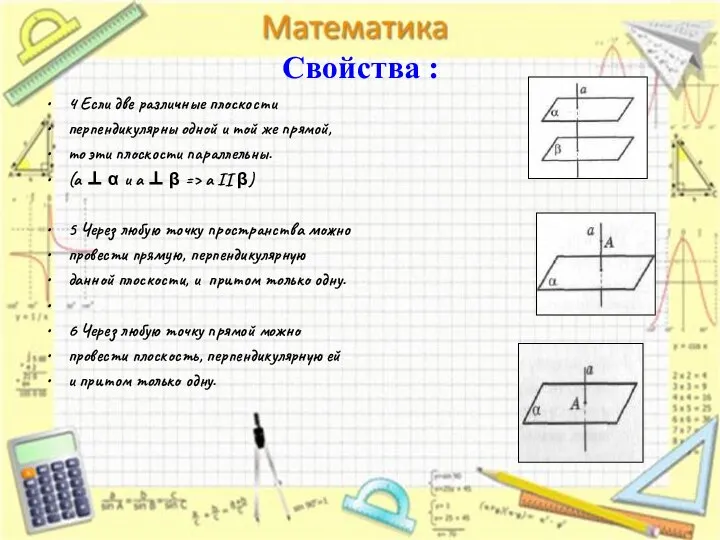
- 6. Свойства : 4 Если две различные плоскости перпендикулярны одной и той же прямой, то эти плоскости
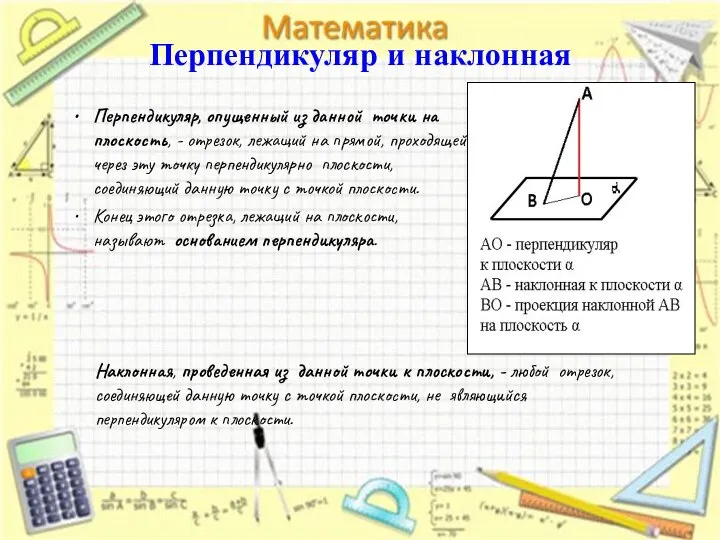
- 7. Перпендикуляр и наклонная Перпендикуляр, опущенный из данной точки на плоскость, - отрезок, лежащий на прямой, проходящей
- 8. Перпендикуляр и наклонная Конец отрезка, лежащий на плоскости, называют основанием наклонной. Отрезок, соединяющий основания перпендикуляра и
- 9. Перпендикуляр и наклонная. 3. Если из одной точки к одной плоскости проведены перпендикуляр и две наклонные,
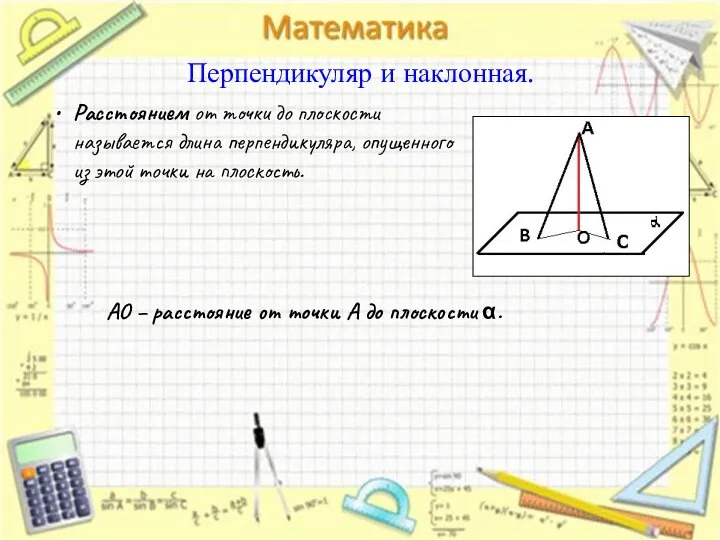
- 10. Перпендикуляр и наклонная. Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на
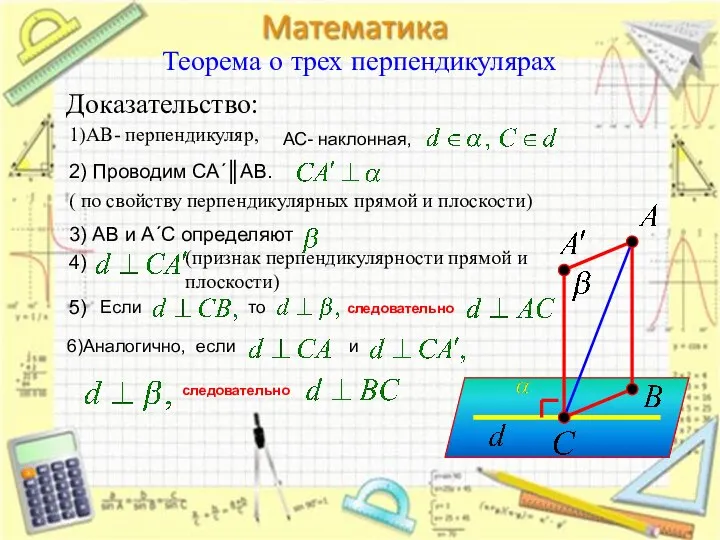
- 11. Теорема о трех перпендикулярах Если прямая, проведенная на плоскости, перпендикулярна проекции наклонной, то она перпендикулярна наклонной
- 12. Теорема о трех перпендикулярах Доказательство: 1)АВ- перпендикуляр, 2) Проводим СА´║АВ. ( по свойству перпендикулярных прямой и
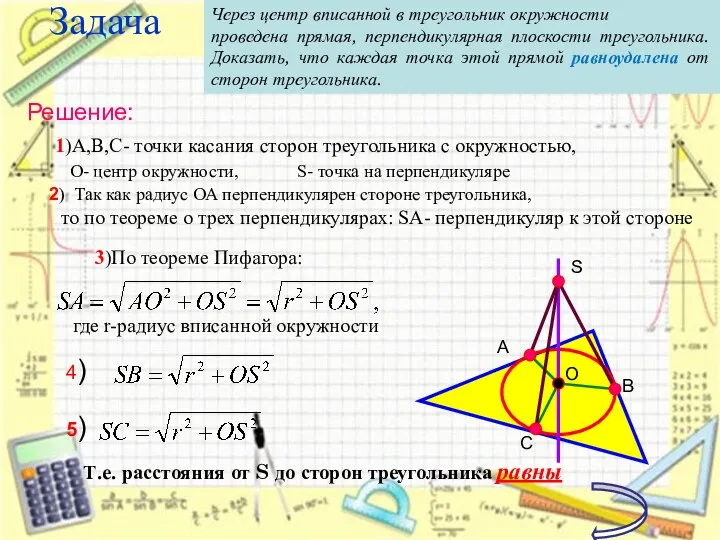
- 13. Задача Т.е. расстояния от S до сторон треугольника равны Через центр вписанной в треугольник окружности проведена
- 14. Перпендикулярность двух плоскостей Перпендикулярные плоскости – две пересекающиеся плоскости, для которых выполняется условие, что третья плоскость,
- 15. Признак перпендикулярности плоскостей Если прямая, лежащая в одной плоскости, перпендикулярна другой плоскости, то эти плоскости перпендикулярны
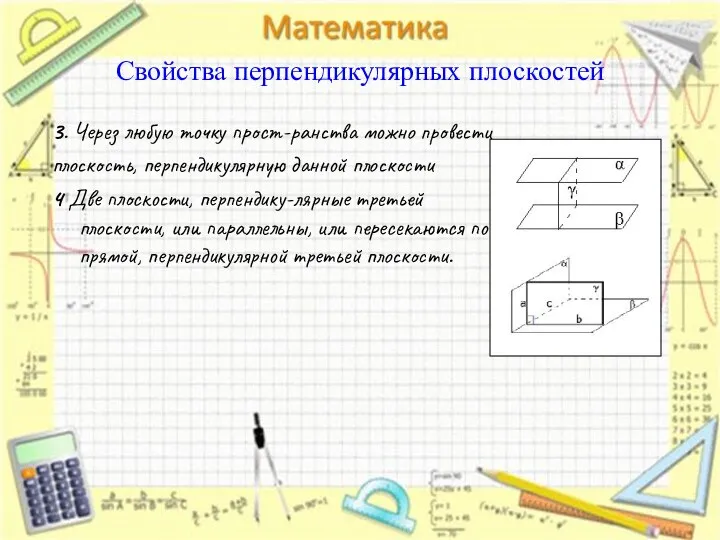
- 16. Свойства перпендикулярных плоскостей 1.Любая плоскость, перпендикуляр-ная прямой пересечения перпенди-кулярных плоскостей, пересекает их по перпендикулярным прямым. (если
- 17. 3. Через любую точку прост-ранства можно провести плоскость, перпендикулярную данной плоскости 4 Две плоскости, перпендику-лярные третьей
- 18. 5. Три попарно перпендику-лярные плоскости пересе-каются по трем перпенди-кулярным прямым (eсли α ⊥β, β ⊥ y,
- 19. Двугранный угол – фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими
- 20. Двугранные углы. Линейный угол двугранного угла – угол, являющийся разрезом этого двугранного угла плоскостью, перпендикулярной ребру
- 21. Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра Общим перпендикуляром двух скрещивающихся прямых называют отрезок
- 23. Скачать презентацию














 Показательная и логарифмическая функции
Показательная и логарифмическая функции Комплексные числа и действия над ними
Комплексные числа и действия над ними Связь деления и умножения
Связь деления и умножения Анализ и синтез как методы научного познания, их применение при обучении математике
Анализ и синтез как методы научного познания, их применение при обучении математике Задания 15 и 4
Задания 15 и 4 Окружность, круг, их элементы и части. Центральный угол
Окружность, круг, их элементы и части. Центральный угол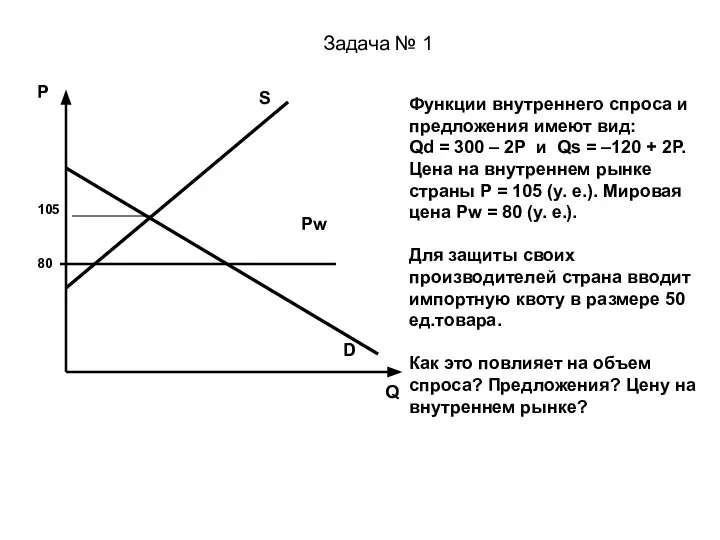 Функции внутреннего спроса и предложения. Разбор задач
Функции внутреннего спроса и предложения. Разбор задач Конус. Виды конусов. Сечения конуса. Площадь боковой поверхности конуса. Площадь полной поверхности конуса
Конус. Виды конусов. Сечения конуса. Площадь боковой поверхности конуса. Площадь полной поверхности конуса Metode numerice. Mulţimea F, de numere în virgulă mobilă este. Curs13
Metode numerice. Mulţimea F, de numere în virgulă mobilă este. Curs13 Розв'язування типових задач
Розв'язування типових задач Презентация на тему Прямоугольник
Презентация на тему Прямоугольник  Презентация на тему Лобачевский и его геометрия
Презентация на тему Лобачевский и его геометрия  Таблица умножения и деления с числом 3
Таблица умножения и деления с числом 3 Логарифмы
Логарифмы ЕГЭ по профильной математике. Прототипы №3
ЕГЭ по профильной математике. Прототипы №3 Индексы пригодности процессов
Индексы пригодности процессов Сфера и шар
Сфера и шар Задания к занятию 1
Задания к занятию 1 Графы. ЕГЭ задание 15. Урок 11 А
Графы. ЕГЭ задание 15. Урок 11 А Алгоритмы. Понятие и свойства алгоритмов
Алгоритмы. Понятие и свойства алгоритмов Нуль без палочки. Математический турнир
Нуль без палочки. Математический турнир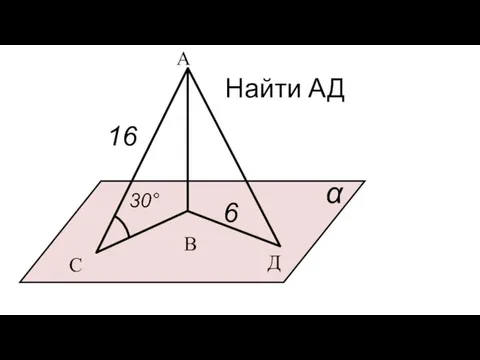 Решение задач
Решение задач Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 3
Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 3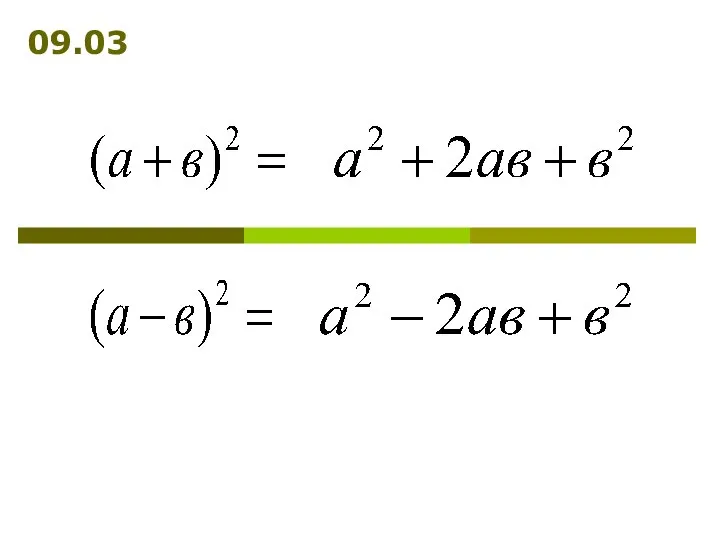 Преобразование многочленов с помощью формул сокращённого умножения
Преобразование многочленов с помощью формул сокращённого умножения Путешествие в звездную математическую страну
Путешествие в звездную математическую страну Решение заданий с параметром. Занятие №1
Решение заданий с параметром. Занятие №1 Практическая работа. Вычислить значения функции в критических точках и на концах отрезка
Практическая работа. Вычислить значения функции в критических точках и на концах отрезка Делители и кратные
Делители и кратные