Содержание
- 2. Числовая окружность на координатной плоскости. ЧТО БУДЕМ ИЗУЧАТЬ: Определение. Важные координаты числовой окружности. Как искать координату
- 3. Определение. Числовая окружность на координатной плоскости. Расположим числовую окружность в координатной плоскости так, чтобы центр окружности
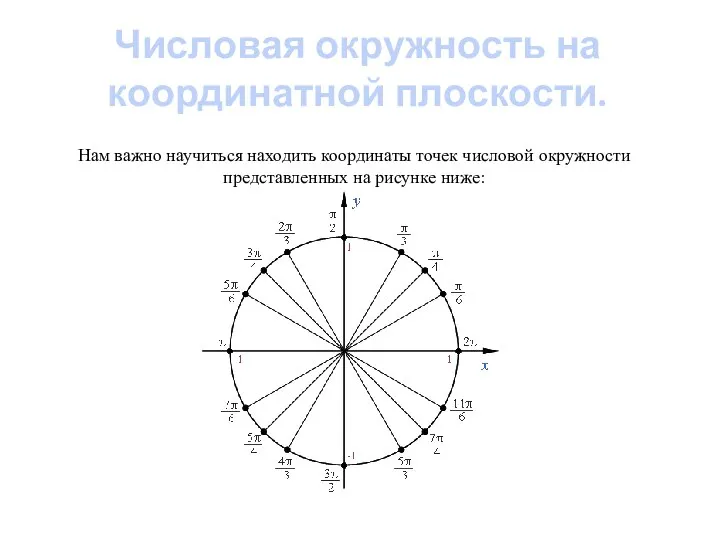
- 4. Числовая окружность на координатной плоскости. Нам важно научиться находить координаты точек числовой окружности представленных на рисунке
- 5. Числовая окружность на координатной плоскости. Найдем координату точки π/4: Точка М(π/4) — середина первой четверти. Опустим
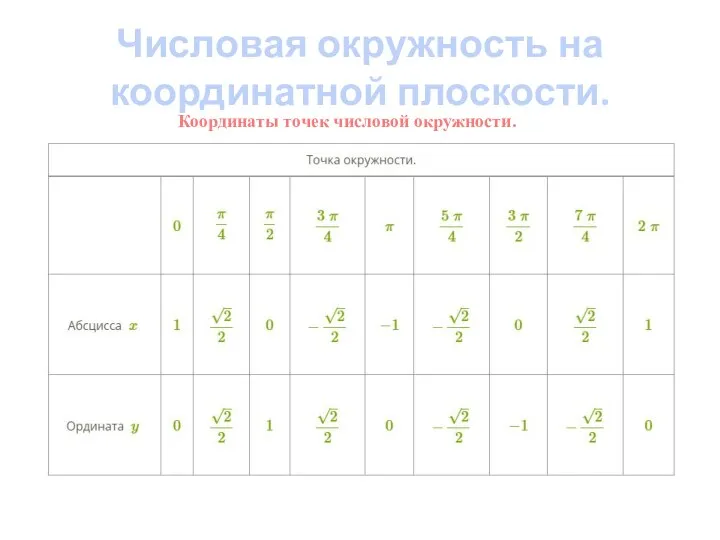
- 6. Координаты точек числовой окружности. Числовая окружность на координатной плоскости.
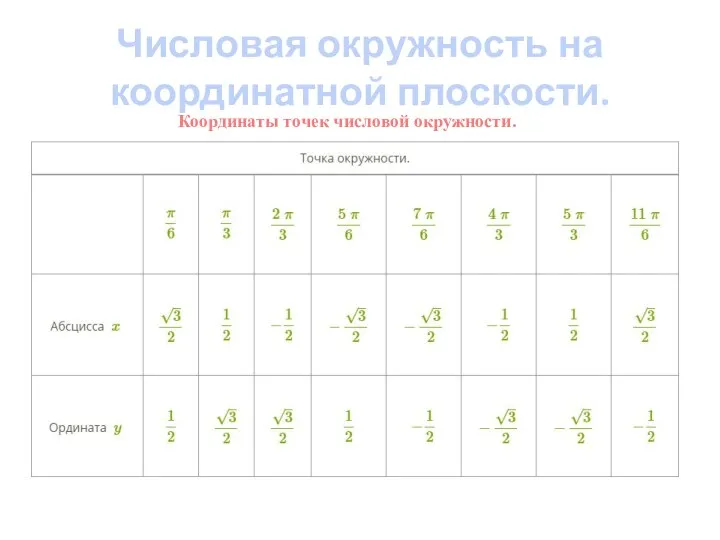
- 7. Координаты точек числовой окружности. Числовая окружность на координатной плоскости.
- 8. Пример Найти координату точки числовой окружности: Р(45π/4) Решение: Т.к. числам t и t+2π•k (k-целое число) соответствует
- 9. Пример Найти координату точки числовой окружности: Р(-37π/3) Решение: Т.к. числам t и t+2π•k (k-целое число) соответствует
- 10. Найти на числовой окружности точки с ординатой у = 1/2 и записать, каким числам t они
- 11. Пример Найти на числовой окружности точки с абсциссой x≥ и записать, каким числам t они соответствуют.
- 13. Скачать презентацию







 Квадратичная функция и ее график
Квадратичная функция и ее график Классификация систем массового обслуживания
Классификация систем массового обслуживания Deterministic finite automata. Nondeterministic finite automata
Deterministic finite automata. Nondeterministic finite automata Математическая интеллектуальная игра для всей семьи
Математическая интеллектуальная игра для всей семьи urok_1_10_klass_geom
urok_1_10_klass_geom Формулы площади
Формулы площади Множество и его элементы
Множество и его элементы Статистический опрос жителей Санкт-Петербурга о применении ими пиротехнических изделий
Статистический опрос жителей Санкт-Петербурга о применении ими пиротехнических изделий Презентация на тему Приемы доказательства неравенств, содержащих переменные
Презентация на тему Приемы доказательства неравенств, содержащих переменные 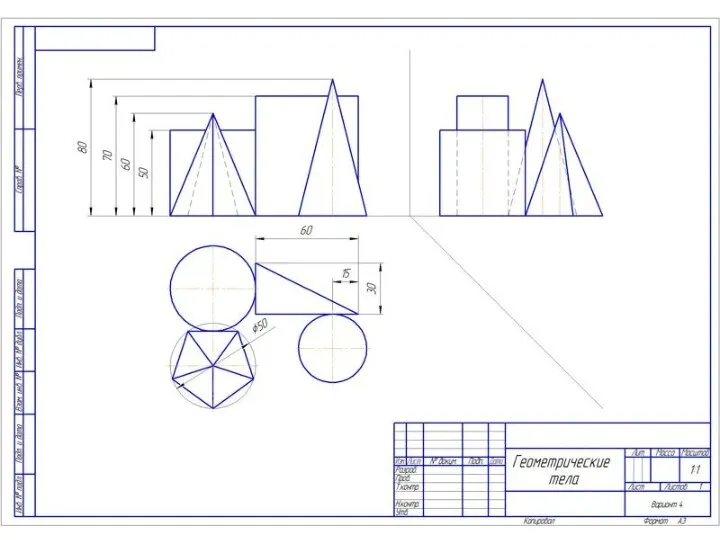 Геометрические тела. 9 класс
Геометрические тела. 9 класс Статистика оплаты труда. Статистическое изучение фонда заработной платы и фонда материального поощрения
Статистика оплаты труда. Статистическое изучение фонда заработной платы и фонда материального поощрения Режим поступления заявок
Режим поступления заявок Презентация на тему Письменное умножение на двузначное число (4 класс)
Презентация на тему Письменное умножение на двузначное число (4 класс)  Основы тригонометрии. Упражнения
Основы тригонометрии. Упражнения Римские Числа Копылова Ольга 6 класс
Римские Числа Копылова Ольга 6 класс Морское путешествие
Морское путешествие Вероятность случайного события. Математика
Вероятность случайного события. Математика Час занимательной математики
Час занимательной математики Частные случаи длины дуги. Лекция №10
Частные случаи длины дуги. Лекция №10 Законы булевой алгебры
Законы булевой алгебры Свойство описанного четырехугольника
Свойство описанного четырехугольника Производная элементарных функций
Производная элементарных функций 20140130_dekada
20140130_dekada Решение уравнений
Решение уравнений Критические точки функции
Критические точки функции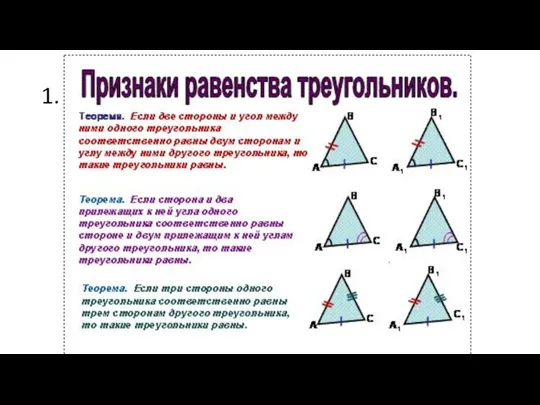 Признаки равенства треугольников
Признаки равенства треугольников Рациональные дроби и их свойства
Рациональные дроби и их свойства Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число