Содержание
- 2. это произведение одинаковых множителей. Выражение αn называют степенью α – n – Степень - основание степени
- 3. Вспомним правила ! Если показатель степени четное число, то значение степени αn всегда ... Если показатель
- 4. Вспомним правила ! Если показатель четное число, то значение степени всегда положительное.
- 5. Вспомним правила ! Если показатель четное число, то значение степени всегда положительное. Если показатель нечетное число,
- 6. Вспомним правила ! Если показатель четное число, то значение степени всегда положительное. отрицательное. Если показатель нечетное
- 7. Вычислите устно 72 23 (-4)2 -42 15 07 33- 52 102 + 82 (10 - 7)3
- 8. Вычислите устно 72 = 49 23 = 8 (-4)2 = 16 -42 = - 16 =
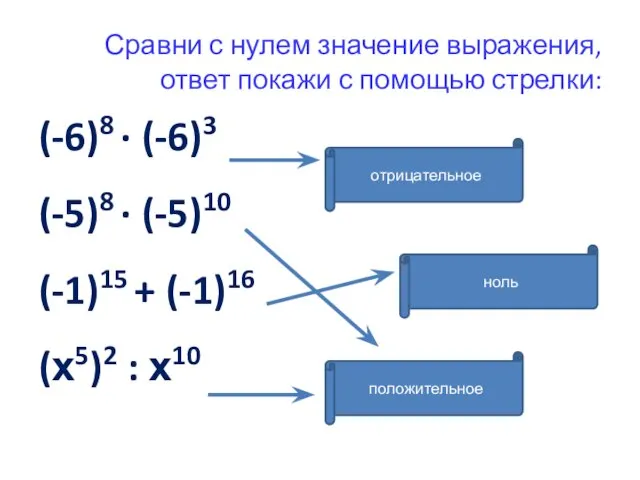
- 9. Сравни с нулем значение выражения, ответ покажи с помощью стрелки: (-6)8 ∙ (-6)3 (-5)8 ∙ (-5)10
- 10. Найди значения выражений Вариант 1. Вариант 2.
- 11. Вариант 1. Вариант 2. Проверь себя = -5 · 9 = - 45 = (- 15)²
- 12. Найдите значение выражений , выберите букву, соответствующую правильному ответу и запишите ее в квадратик: b2 –
- 13. а показатели степеней сложить. аn · аk = аn+k Вспомним свойства степени! 1. Произведение степеней :
- 14. а показатели вычесть. а n : а k = а n - k 2. Частное степеней
- 15. а показатели степеней перемножить. (аn)к = аnk 3. Возведение степени в степень (п.20) При возведении степени
- 16. 4. Возведение в степень произведения (п.20) возвести в эту степень каждый множитель
- 17. Представьте выражение в виде степени ( упростите ). х5 ∙ х7 (a3)5 5 ∙ 52 (3х2)3
- 18. Проверьте . х5 ∙ х7 = х¹²; (a3)5= a¹5 ; 5 ∙ 52 =125; (3х2)3 =27х⁶;
- 19. Какое число надо поставить вместо *, чтобы получилось верное равенство. 1) х8 : х* = х4
- 20. Проверка. получилось верное равенство. 1) х8 : х4 = х4 ; х22 = х ∙ х21
- 21. Вычислите : 3∙3∙3∙3∙3 = 81 = 120 = 52 · 53 = 25 · 2³ =
- 22. Вычислите : 1) 3∙3∙3∙3∙3 = 3⁵ = 243 2) 81= 3) 120 = 1 4) 52
- 23. Вариант 1. Самостоятельная работа Вариант 2
- 25. Скачать презентацию





















 Доказательство клауз. Лекция 7
Доказательство клауз. Лекция 7 Геометрические преобразования графиков функций
Геометрические преобразования графиков функций Презентация на тему Расстояние от точки до плоскости
Презентация на тему Расстояние от точки до плоскости  Funktsia_osnovnye_svoi_774_stva
Funktsia_osnovnye_svoi_774_stva Начальные геометрические сведения. Параллельные прямые
Начальные геометрические сведения. Параллельные прямые Практическое. Занятие № 7. Численные методы решения задачи коши
Практическое. Занятие № 7. Численные методы решения задачи коши d694e47421834013895052f206be4c31
d694e47421834013895052f206be4c31 Свойства числовых неравенств
Свойства числовых неравенств Математика вокруг нас узоры и орнаменты на посуде
Математика вокруг нас узоры и орнаменты на посуде Презентация на тему Наибольший общий делитель (6 класс)
Презентация на тему Наибольший общий делитель (6 класс) 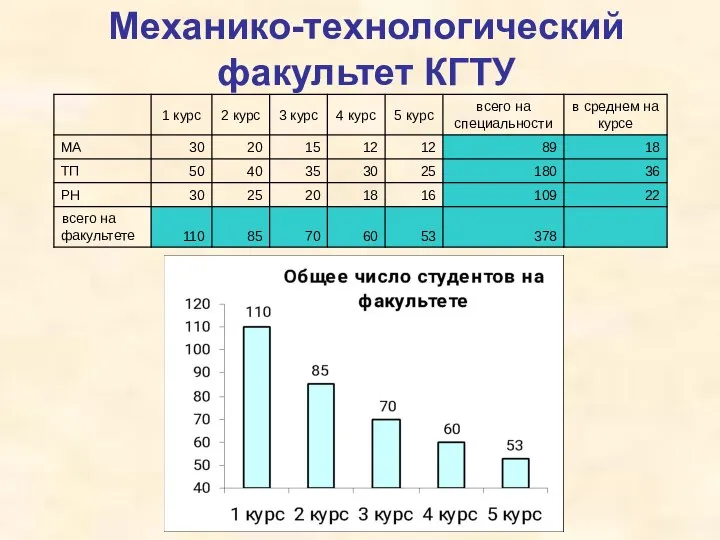 Диаграммы
Диаграммы Показательные уравнения
Показательные уравнения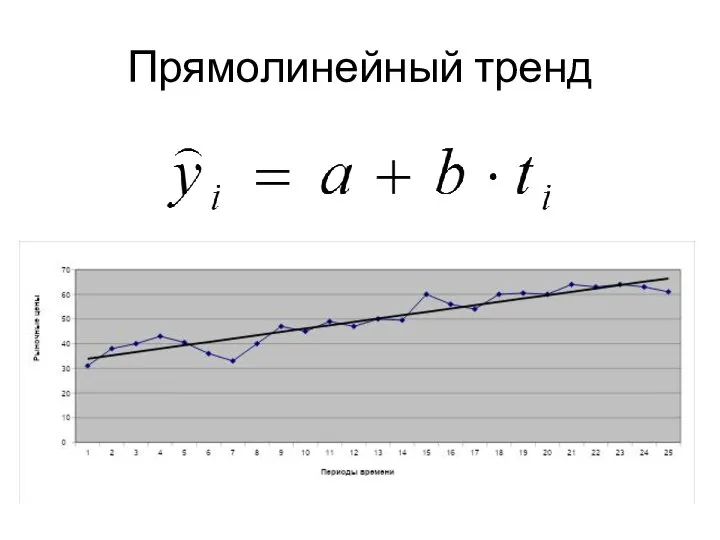 Прямолинейный тренд
Прямолинейный тренд Параллельность в пространстве
Параллельность в пространстве Дроби
Дроби Элементы математического анализа
Элементы математического анализа Площадь параллелограмма
Площадь параллелограмма Презентация на тему Решение уравнения sin t = a
Презентация на тему Решение уравнения sin t = a  Задачи на построение
Задачи на построение Случаи вычитания 12 -
Случаи вычитания 12 - Измерение объема жидких и сыпучих веществ с помощью условной меры масс
Измерение объема жидких и сыпучих веществ с помощью условной меры масс Семинар по математике
Семинар по математике Первая теорема сравнения
Первая теорема сравнения Область определения функции. 9 класс
Область определения функции. 9 класс Корень уравнения
Корень уравнения График функции
График функции Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Морское путешествие
Морское путешествие