Сечения в многогранниках

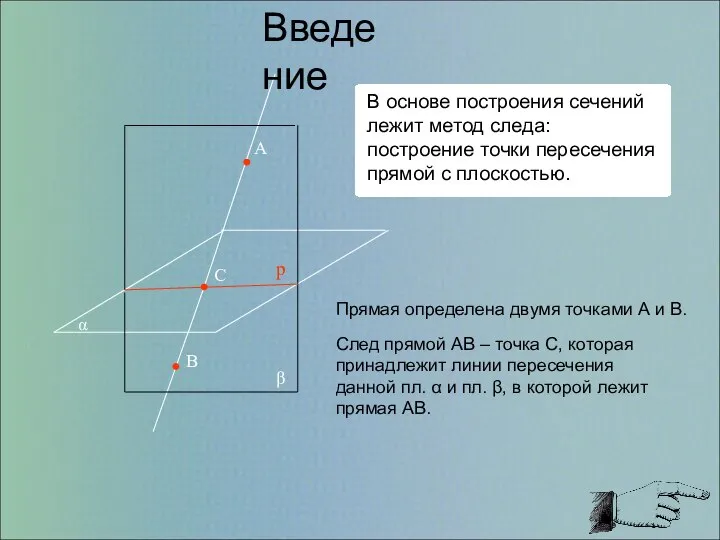
α
β
A
B
C
p
Введение
Прямая определена двумя точками А и В.
След прямой АВ – точка С, которая принадлежит линии пересечения данной пл. α и пл. β, в которой лежит прямая АВ.

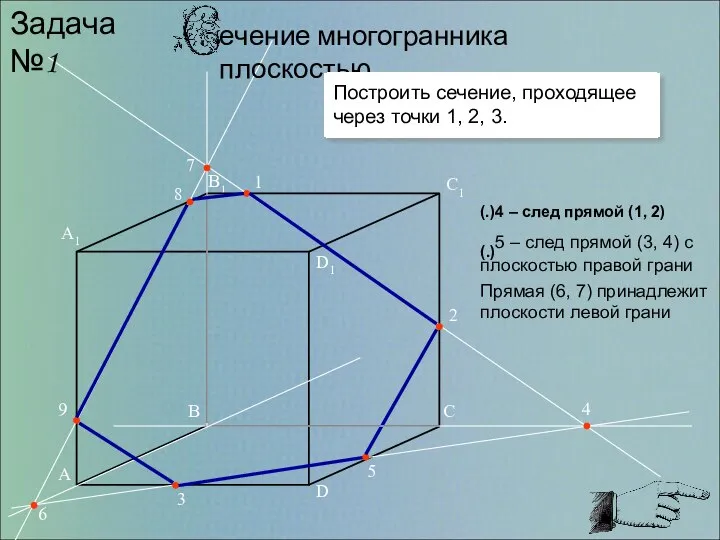
1
2
3
4
5
6
7
8
9
Задача №1
(.)4 – след прямой (1, 2)
(.)5 – след прямой (3, 4) с плоскостью правой грани
Прямая (6, 7) принадлежит плоскости левой грани

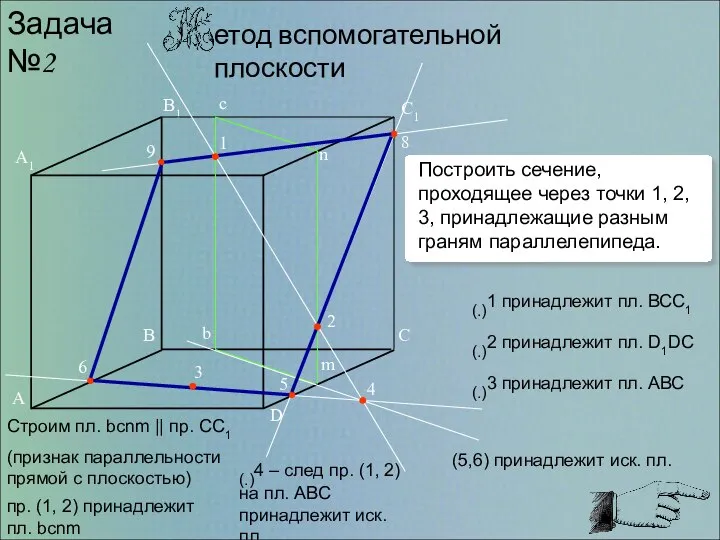
b
c
n
m
1
2
3
4
5
6
8
9
Задача №2
(.)1 принадлежит пл. ВСС1
(.)2 принадлежит пл. D1DC
(.)3 принадлежит пл. АВС
Строим пл. bcnm || пр. СС1
(признак параллельности прямой с плоскостью)
пр. (1, 2) принадлежит пл. bcnm
(.)4 – след пр. (1, 2) на пл. АВС принадлежит иск. пл.
(5,6) принадлежит иск. пл.

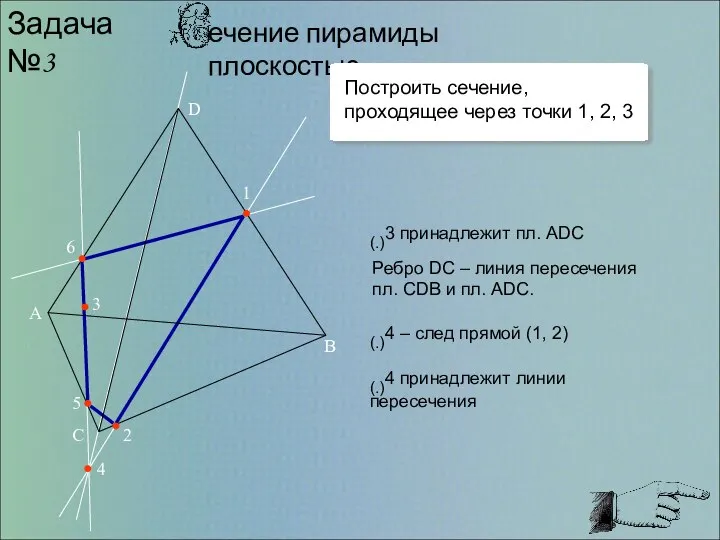
A
B
C
D
1
2
3
4
5
6
Задача №3
(.)3 принадлежит пл. ADC
(.)4 – след прямой (1, 2)
Ребро DC – линия пересечения пл. CDB и пл. ADC.
(.)4 принадлежит линии пересечения

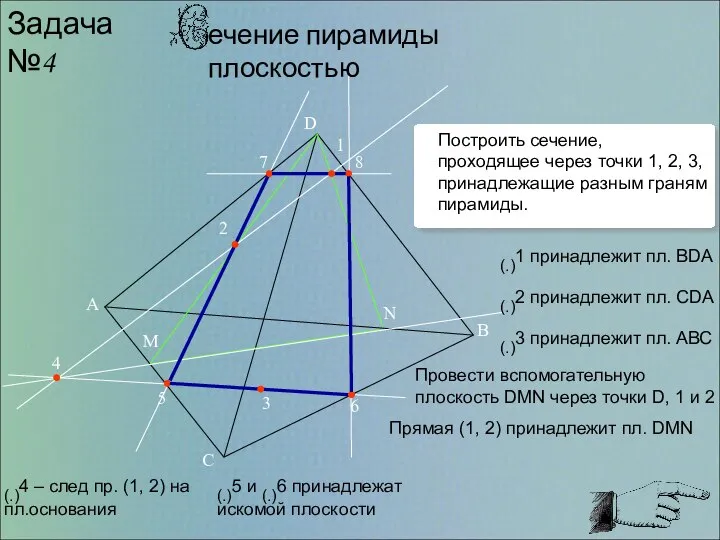
N
M
1
2
3
4
5
6
7
8
Задача №4
(.)1 принадлежит пл. BDA
(.)2 принадлежит пл. CDA
(.)3 принадлежит пл. АВС
Провести вспомогательную плоскость DMN через точки D, 1 и 2
Прямая (1, 2) принадлежит пл. DMN
(.)4 – след пр. (1, 2) на пл.основания
(.)5 и (.)6 принадлежат искомой плоскости

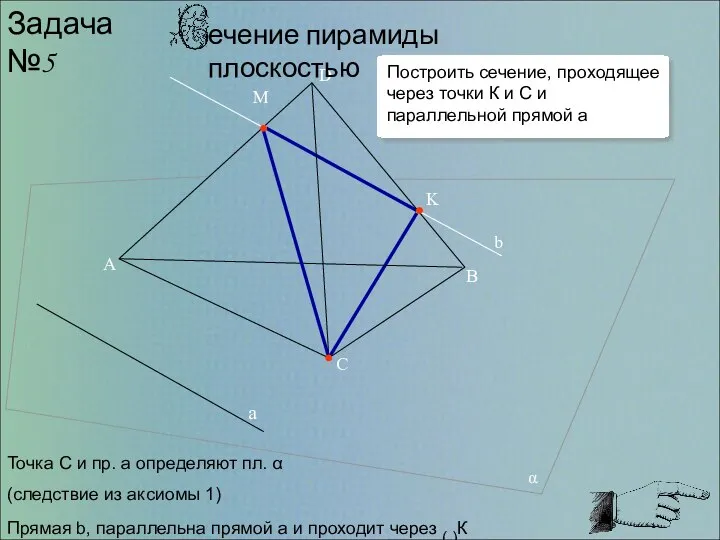
α
K
M
a
b
Задача №5
Прямая b, параллельна прямой а и проходит через (.)К
Точка С и пр. а определяют пл. α
(следствие из аксиомы 1)

В основе построения сечения лежит метод следа.
Если две точки секущей плоскости α лежат в плоскости одной грани, то проводим через них прямую. Часть прямой в грани является стороной сечения.
Если «а» - общая прямая секущей плоскости и плоскости грани, то находим точки пересечения прямой «а» с прямыми, содержащими рёбра этой грани, т.е. след прямой «а» на соседнюю грань.
Если никакие две точки сечения не лежат в одной грани, то строим вспомогательное сечение, содержащее данные точки