Содержание
- 2. Задачи урока:
- 3. “В своей жизни человек обязательно должен сделать три вещи: посадить дерево, построить дом и вырастить сына”
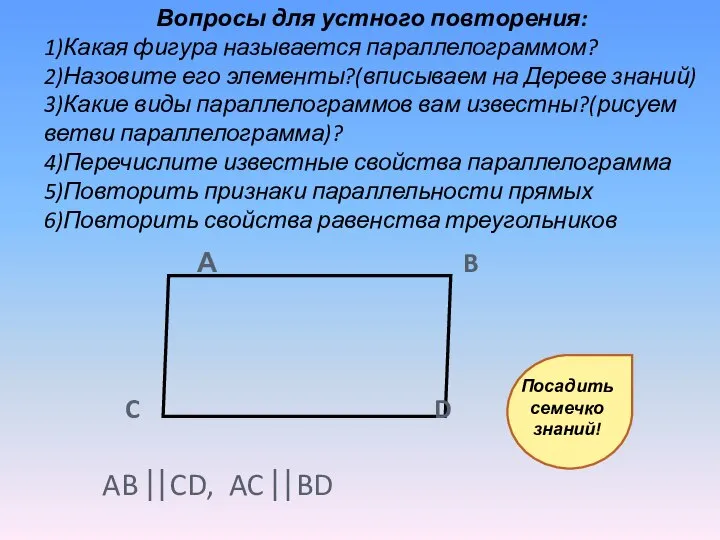
- 4. А B C D AB ⎢⎢CD, AC ⎢⎢BD Вопросы для устного повторения: 1)Какая фигура называется параллелограммом?
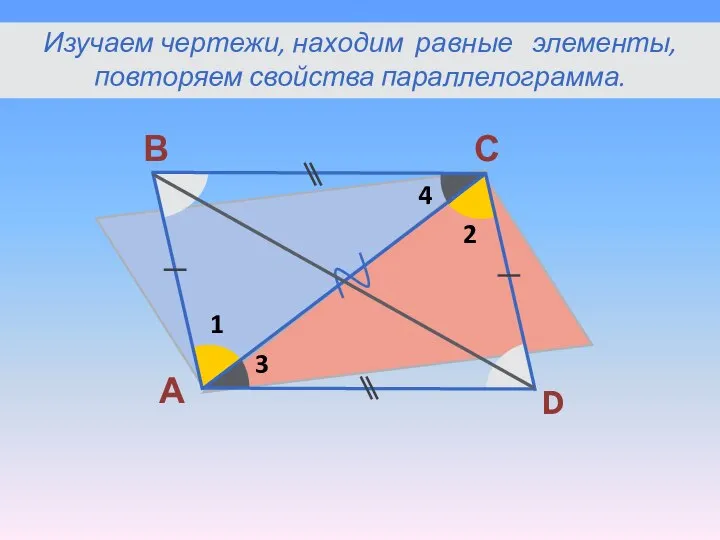
- 5. А В С D 1 2 3 4 Изучаем чертежи, находим равные элементы, повторяем свойства параллелограмма.
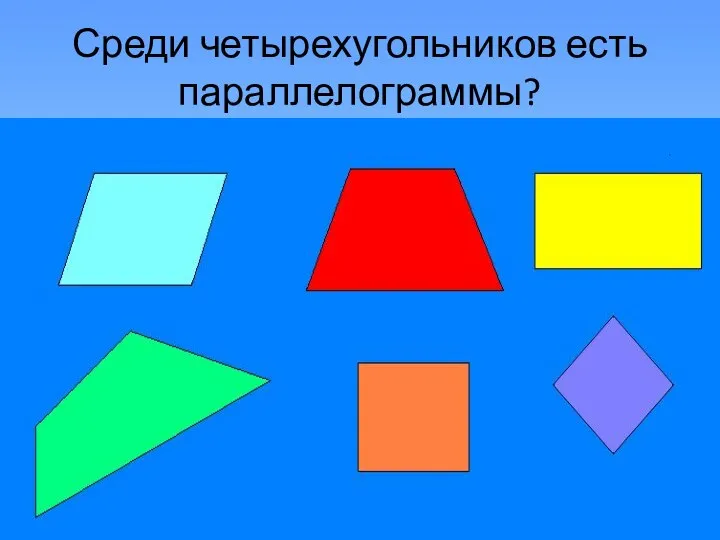
- 6. Среди четырехугольников есть параллелограммы?
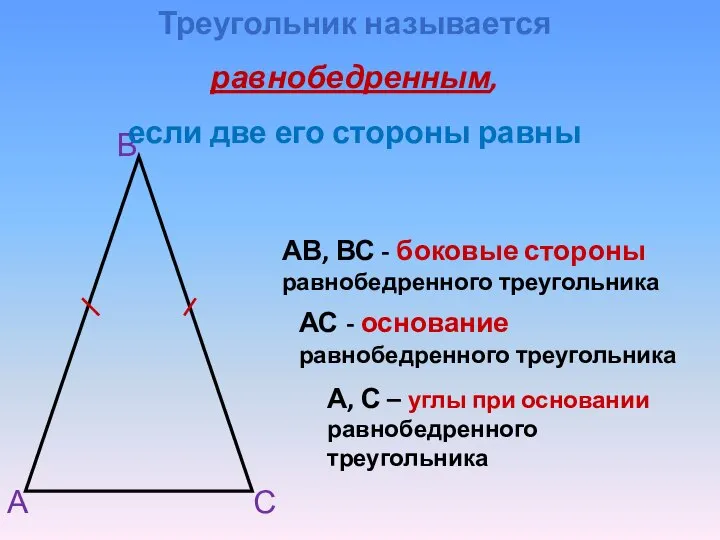
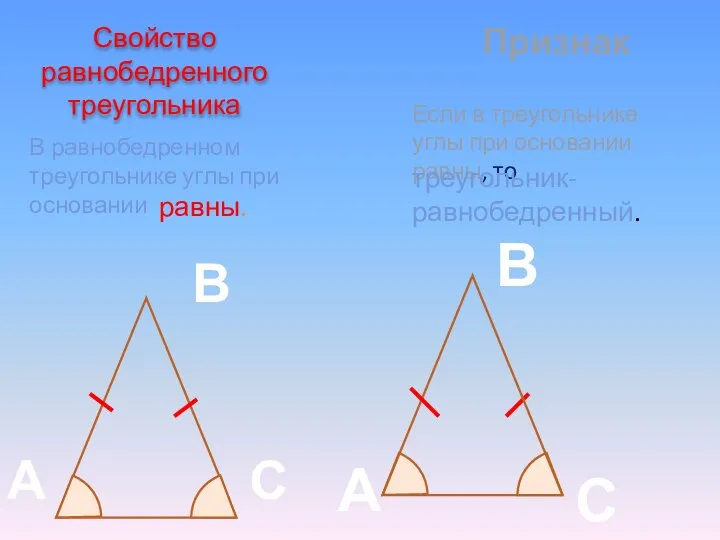
- 7. А В С АВ, ВС - боковые стороны равнобедренного треугольника А, С – углы при основании
- 8. Свойство равнобедренного треугольника В С В равнобедренном треугольнике углы при основании Признак Если в треугольнике углы
- 9. Свойство Признак ? Обратная теорема Определение
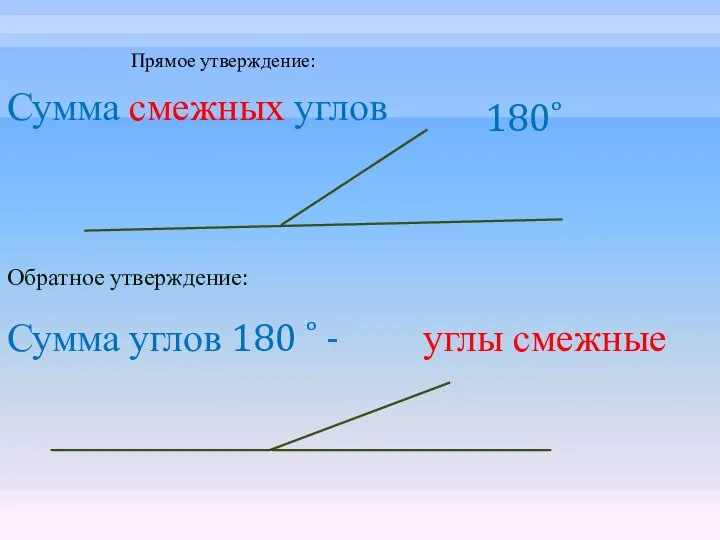
- 10. Сумма смежных углов 180˚ Сумма углов 180 ˚ - Прямое утверждение: Обратное утверждение: углы смежные
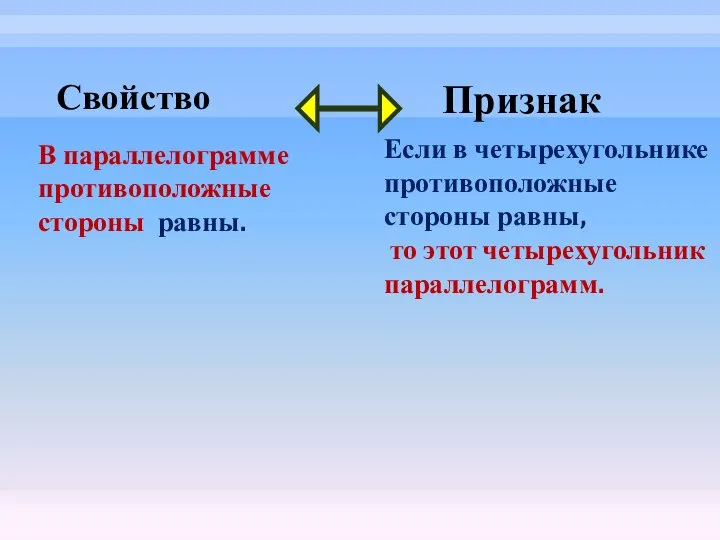
- 11. В параллелограмме противоположные стороны равны. Если в четырехугольнике противоположные стороны равны, то этот четырехугольник параллелограмм. Свойство
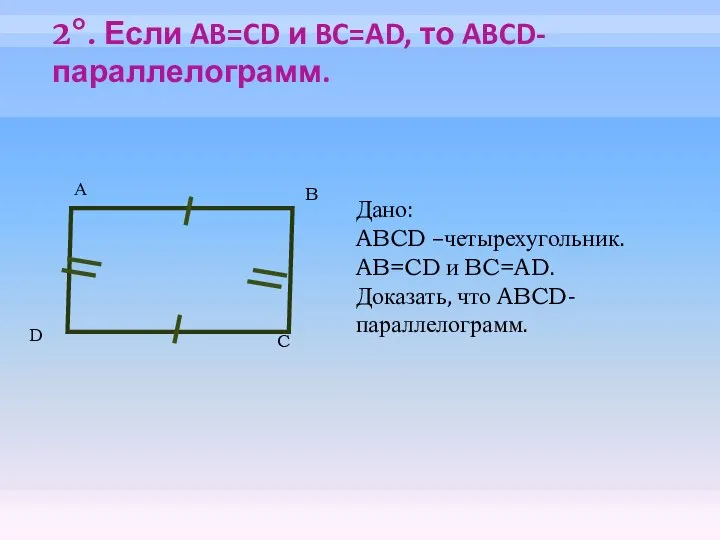
- 12. 2°. Если AB=CD и BC=AD, то ABCD-параллелограмм. А B C Дано: ABCD –четырехугольник. AB=CD и BC=AD.
- 13. В параллелограмме диагонали точкой пересечения делятся пополам. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то
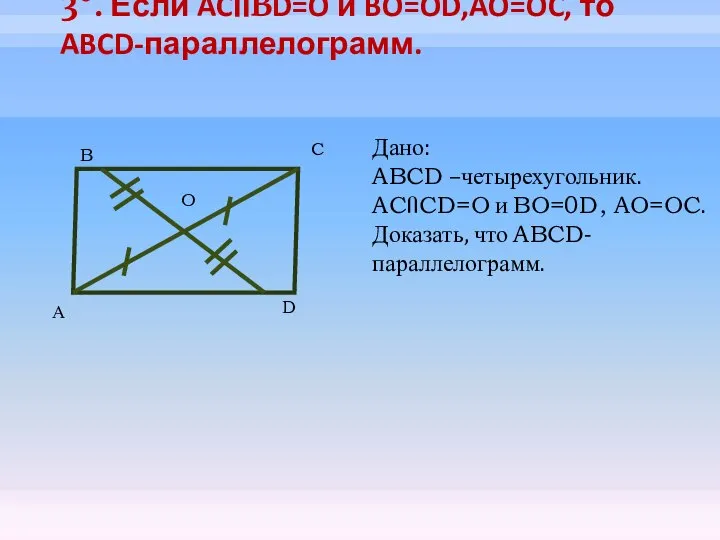
- 14. 3°. Если ACՈBD=O и BO=OD,AO=OC, то ABCD-параллелограмм. А B C D Дано: ABCD –четырехугольник. ACՈCD=O и
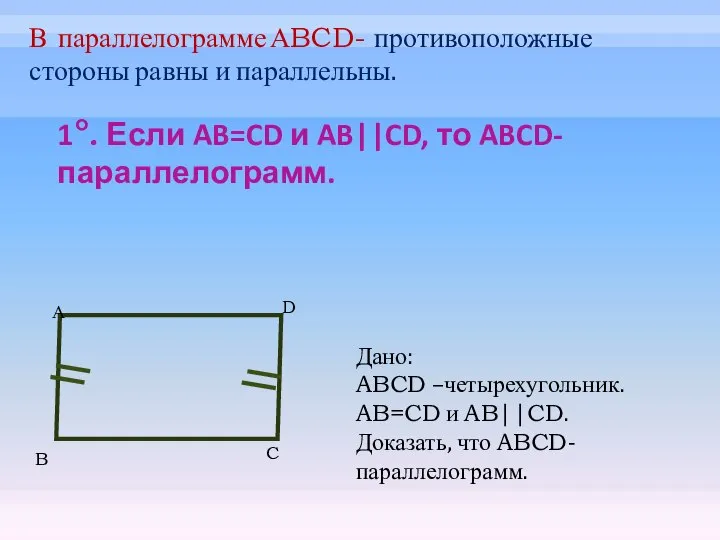
- 15. 1°. Если AB=CD и AB||CD, то ABCD-параллелограмм. А B C D Дано: ABCD –четырехугольник. AB=CD и
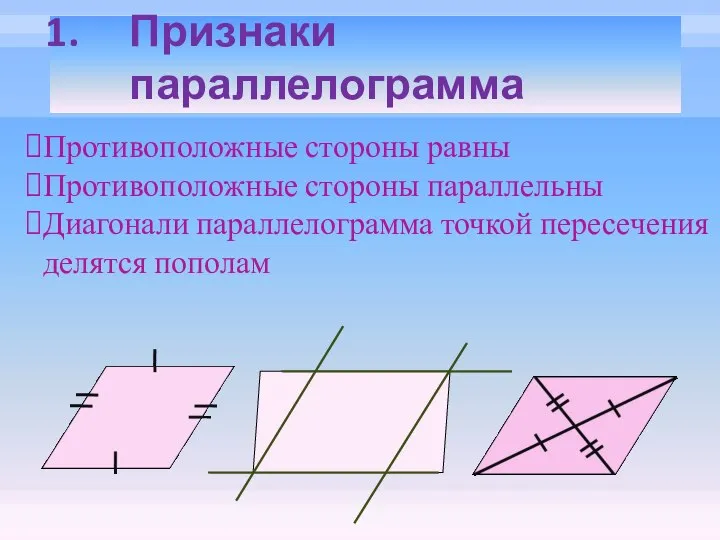
- 16. Признаки параллелограмма Противоположные стороны равны Противоположные стороны параллельны Диагонали параллелограмма точкой пересечения делятся пополам
- 17. МУЗЫКАЛЬНАЯ ПАУЗА
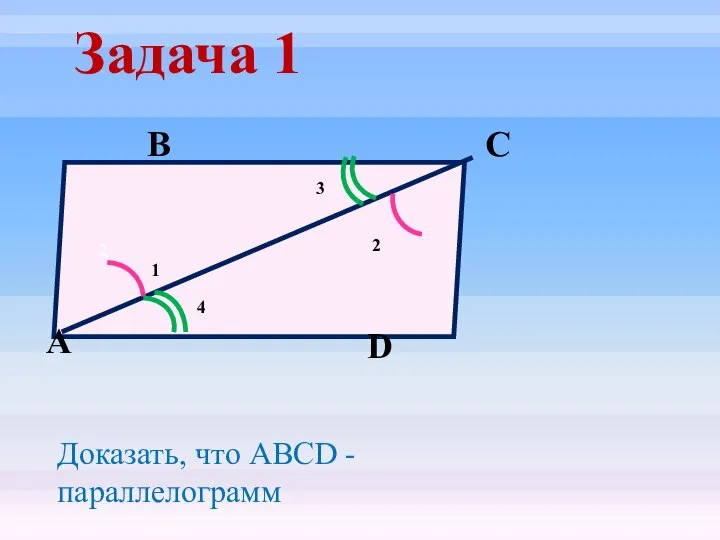
- 18. Задача 1 2 D С В А Доказать, что ABCD - параллелограмм 1 2 4 3
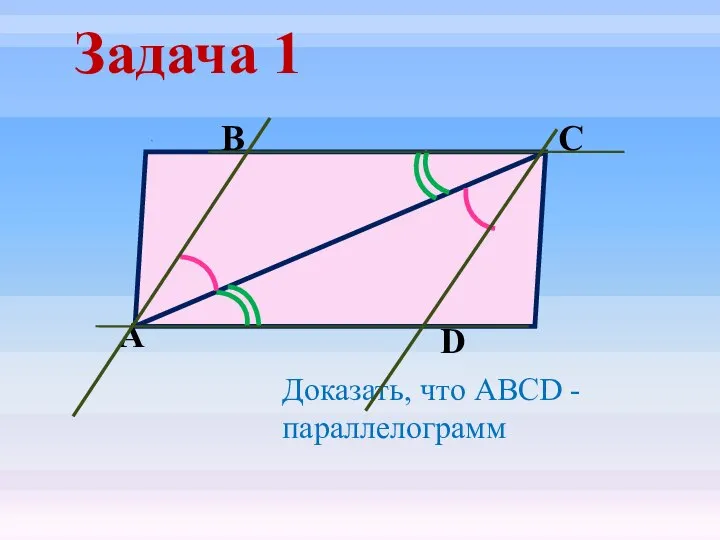
- 19. Задача 1 D С В А Доказать, что ABCD - параллелограмм
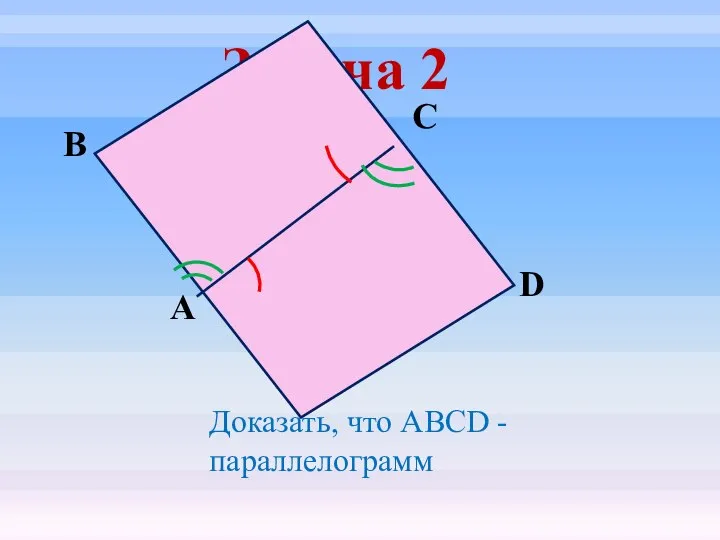
- 20. Задача 2 D С В А Доказать, что ABCD - параллелограмм
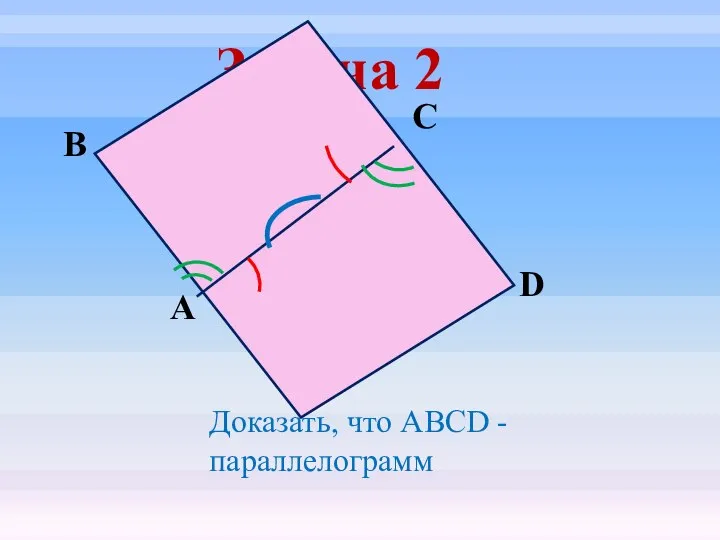
- 21. Задача 2 D С В А Доказать, что ABCD - параллелограмм
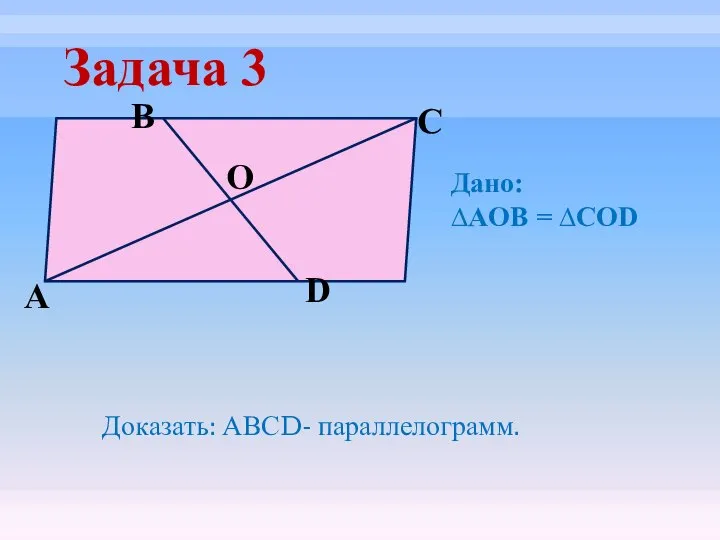
- 22. Задача 3 O D C B А Доказать: АВСD- параллелограмм. Дано: ∆AOB = ∆COD
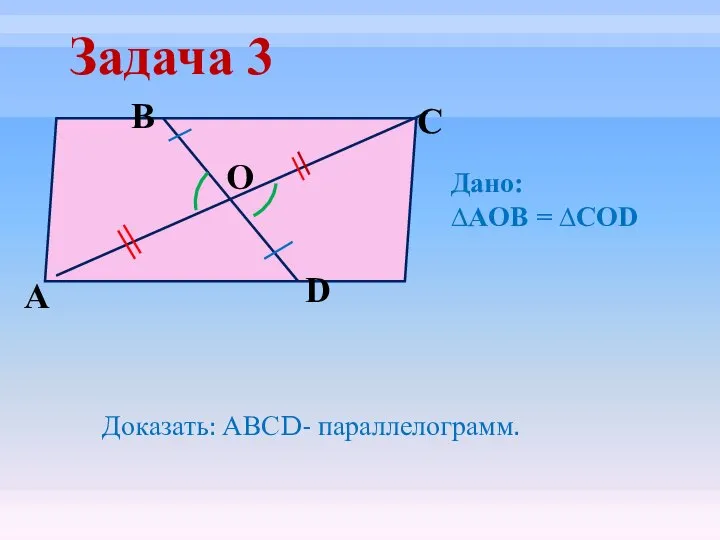
- 23. Задача 3 O D C B А Доказать: АВСD- параллелограмм. Дано: ∆AOB = ∆COD
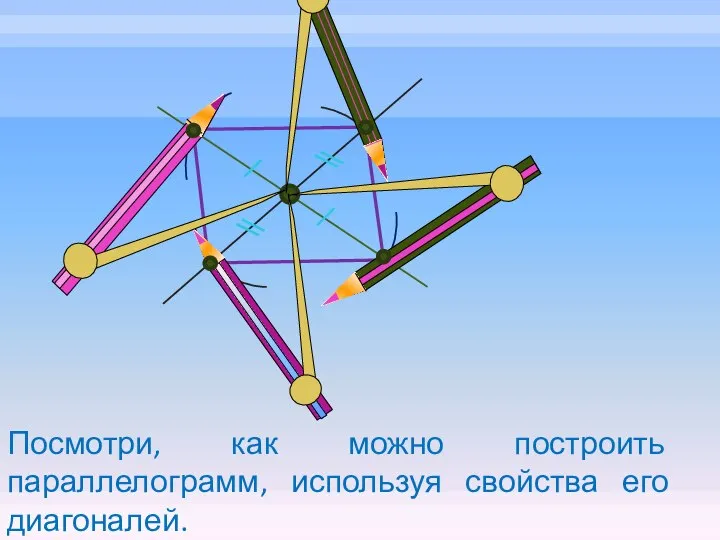
- 24. Посмотри, как можно построить параллелограмм, используя свойства его диагоналей.
- 25. красный – радость зелёный – спокойствие жёлтый – тревога чёрный – разочарование ВАШЕ НАСТРОЕНИЕ
- 26. Параллелограммы Элементы параллелограмма Вершины Углы Стороны Свойства параллелограмма Признаки параллелограмма Большим и сильным вырастет наше Дерево
- 28. Скачать презентацию






 Степень, графики функций, пропорции на уроках математики и физики
Степень, графики функций, пропорции на уроках математики и физики Параллельность прямой и плоскости
Параллельность прямой и плоскости Обратные тригонометрические функции
Обратные тригонометрические функции О построении дерева Хаффмана
О построении дерева Хаффмана MV1_Lektsia_2_-_Predstavlenie_nechetkikh_znaniy_-_kopia
MV1_Lektsia_2_-_Predstavlenie_nechetkikh_znaniy_-_kopia Презентация на тему Платоновы тела Правильные выпуклые многогранники 10 класс
Презентация на тему Платоновы тела Правильные выпуклые многогранники 10 класс  Наглядная геометрия. Деление области с помощью линий1 класс
Наглядная геометрия. Деление области с помощью линий1 класс Планиметрия. Обзор методички
Планиметрия. Обзор методички Формула Пика
Формула Пика Обозначение и сравнение углов
Обозначение и сравнение углов Построение графиков функций
Построение графиков функций Метод интервалов в решении неравенств
Метод интервалов в решении неравенств Деление дробей. Контрольная работа
Деление дробей. Контрольная работа С чего начать подготовку к ЕГЭ по профильной математике
С чего начать подготовку к ЕГЭ по профильной математике Некоторые свойства прямоугольных треугольников. Решение задач
Некоторые свойства прямоугольных треугольников. Решение задач Таблица для мешка по двум признакам
Таблица для мешка по двум признакам Презентация на тему Умножение и деление на 10 и 100
Презентация на тему Умножение и деление на 10 и 100  Сумма углов в треугольнике
Сумма углов в треугольнике Средняя линия треугольника
Средняя линия треугольника Уравнение с двумя переменными и его график
Уравнение с двумя переменными и его график Пропорции в нашем мире
Пропорции в нашем мире Решение задач на нахождение площади фигур. 6 класс
Решение задач на нахождение площади фигур. 6 класс Исследование корреляции
Исследование корреляции Квадратный трехчлен и его корни Программа элективного курса по математике для 8-9 классов в рамках предпрофильной подготовки
Квадратный трехчлен и его корни Программа элективного курса по математике для 8-9 классов в рамках предпрофильной подготовки Математика. 1 класс
Математика. 1 класс Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Симметрия. Закономерности
Симметрия. Закономерности Построение желаемой ЛАЧХ разомкнутой системы в частотном методе синтеза корректирующего звена
Построение желаемой ЛАЧХ разомкнутой системы в частотном методе синтеза корректирующего звена