Содержание
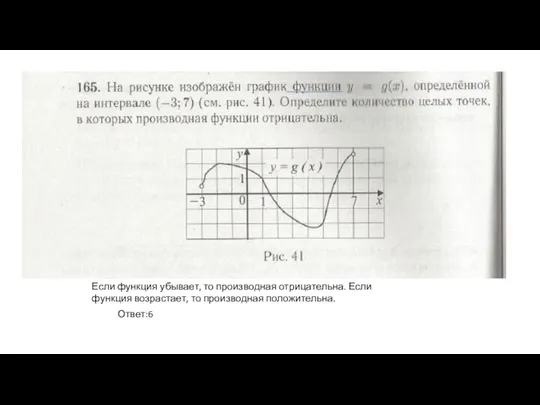
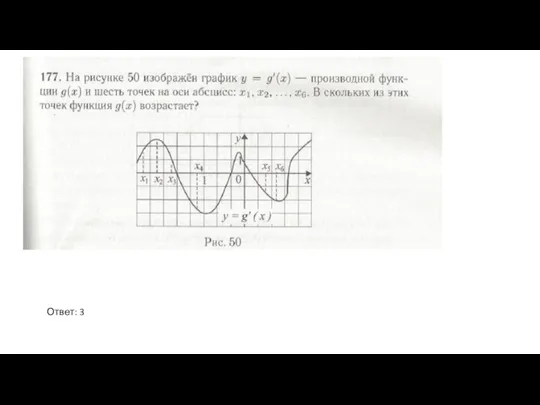
- 2. Если функция убывает, то производная отрицательна. Если функция возрастает, то производная положительна. Ответ:6
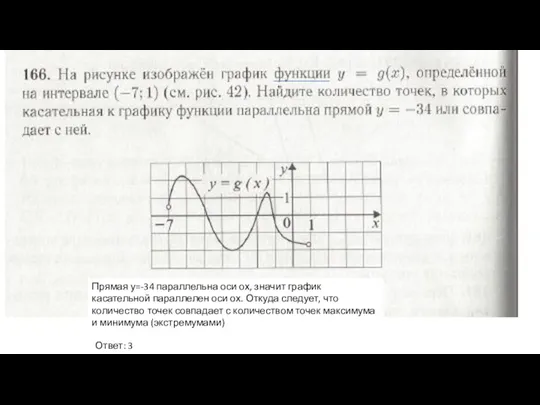
- 3. Ответ: 3 Прямая у=-34 параллельна оси ох, значит график касательной параллелен оси ох. Откуда следует, что
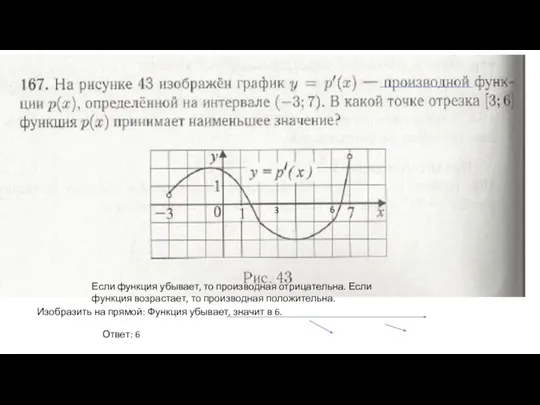
- 4. Изобразить на прямой: Функция убывает, значит в 6. Ответ: 6 3 6 Если функция убывает, то
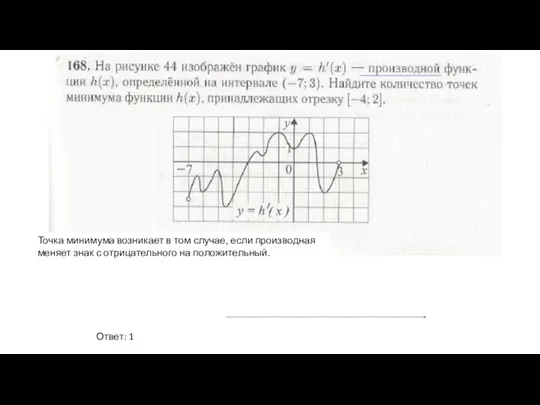
- 5. Ответ: 1 Точка минимума возникает в том случае, если производная меняет знак с отрицательного на положительный.
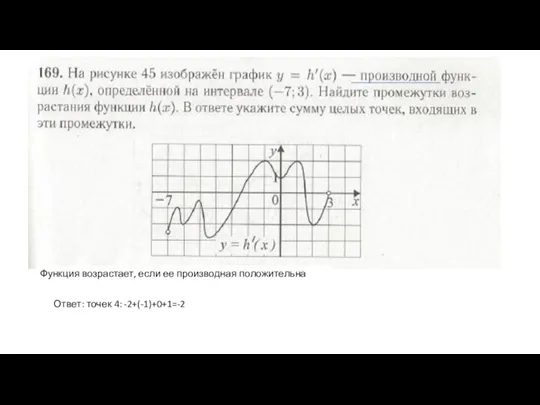
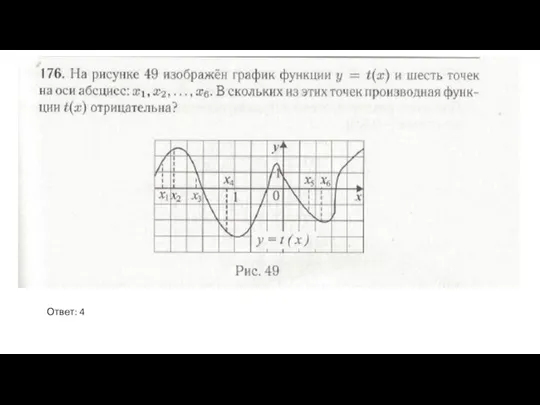
- 6. Функция возрастает, если ее производная положительна Ответ: точек 4: -2+(-1)+0+1=-2
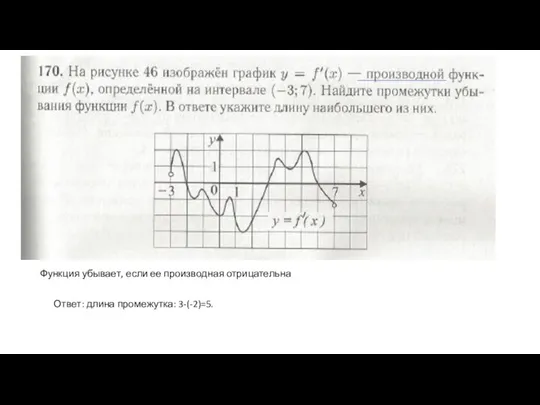
- 7. Функция убывает, если ее производная отрицательна Ответ: длина промежутка: 3-(-2)=5.
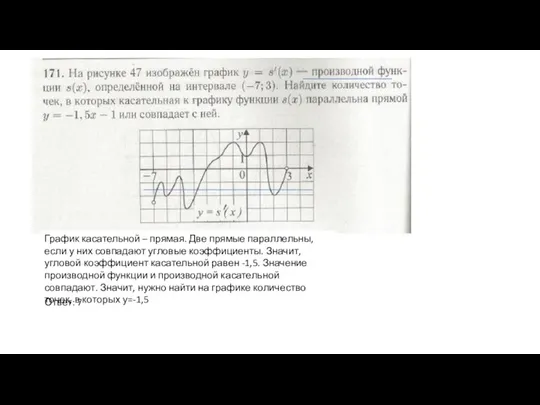
- 8. График касательной – прямая. Две прямые параллельны, если у них совпадают угловые коэффициенты. Значит, угловой коэффициент
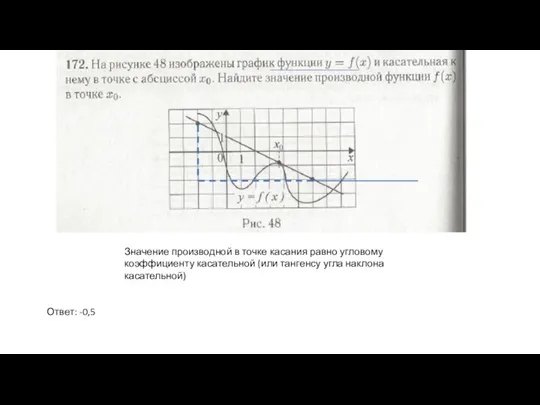
- 9. Значение производной в точке касания равно угловому коэффициенту касательной (или тангенсу угла наклона касательной) Ответ: -0,5
- 10. В точке касания значения производных касательной и функции и значения самих функций (касательной и функции) совпадают.
- 11. Ответ: 21
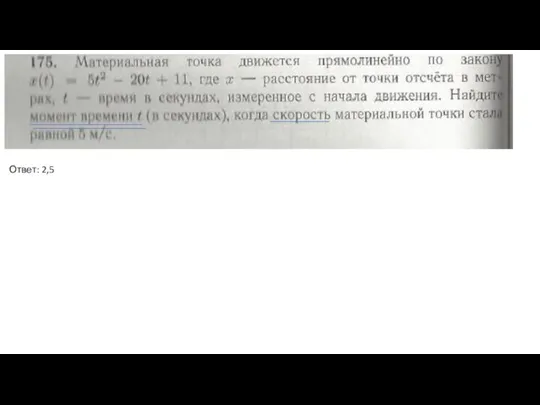
- 12. Ответ: 2,5
- 13. Ответ: 4
- 14. Ответ: 3
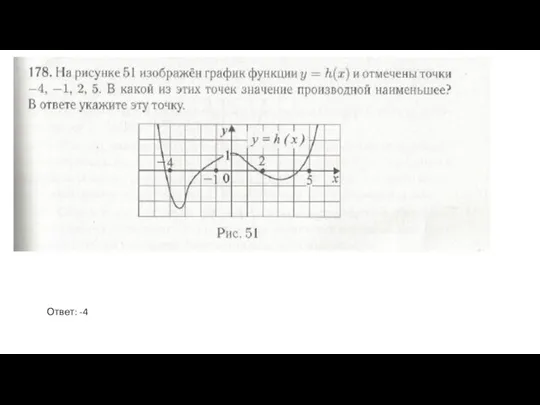
- 15. Ответ: -4
- 16. Ответ: 3
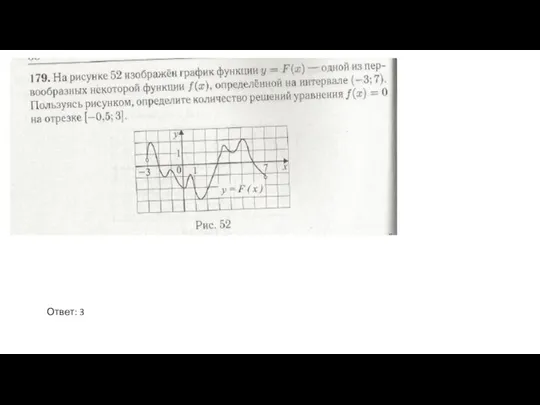
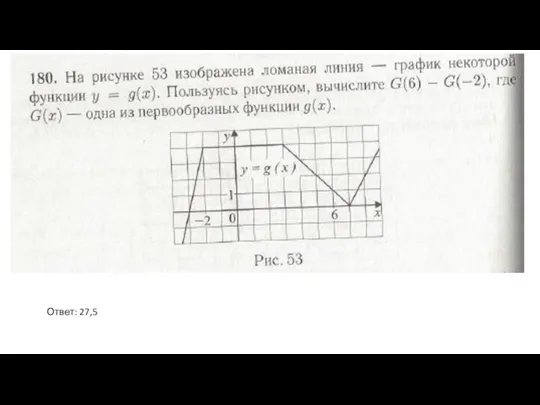
- 17. Ответ: 27,5
- 19. Скачать презентацию


 Государственное общеобразовательное учреждение Гимназия№49 Приморского района Санкт -Петербурга «Путешествие Алисы в страну Ма
Государственное общеобразовательное учреждение Гимназия№49 Приморского района Санкт -Петербурга «Путешествие Алисы в страну Ма Основы функционального анализа
Основы функционального анализа Алгебраические и геометрические модели
Алгебраические и геометрические модели Прямая и окружность
Прямая и окружность Решение задач на построение методом подобных треугольников
Решение задач на построение методом подобных треугольников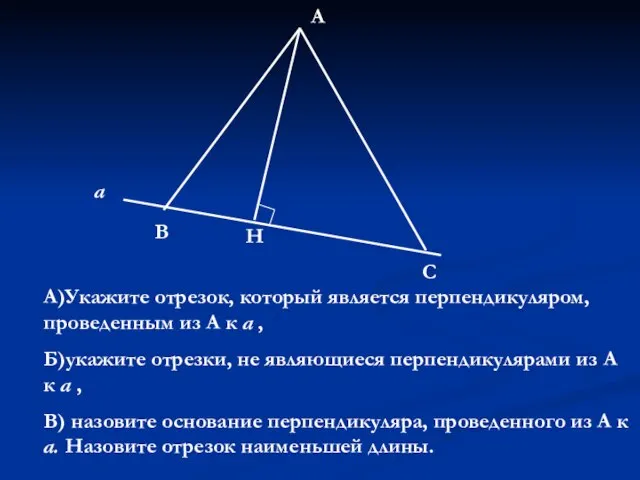 Построение треугольника
Построение треугольника Векторы. Обобщающий урок
Векторы. Обобщающий урок Решение логарифмических уравнений
Решение логарифмических уравнений Уравнение древности. Франсуа Виет
Уравнение древности. Франсуа Виет Решение уравнений и неравенств с модулем
Решение уравнений и неравенств с модулем Решение задач на применение аксиом стереометрии и их следствий
Решение задач на применение аксиом стереометрии и их следствий Параллелепипед. Куб
Параллелепипед. Куб Элементы комбинаторики
Элементы комбинаторики Решение начально-краевой задачи для линейного уравнения теплопроводности разностным методом. Практическое занятие №8
Решение начально-краевой задачи для линейного уравнения теплопроводности разностным методом. Практическое занятие №8 Шар и сфера
Шар и сфера Нумерация. Сложение и вычитание. Геометрические фигуры и величины
Нумерация. Сложение и вычитание. Геометрические фигуры и величины Диференціальні рівняння
Диференціальні рівняння Отрезок, луч, прямая. Графический диктант 1. 5 класс
Отрезок, луч, прямая. Графический диктант 1. 5 класс Презентация на тему ДЕЛИТЕЛИ И КРАТНЫЕ
Презентация на тему ДЕЛИТЕЛИ И КРАТНЫЕ  Формулы сокращенного умножения a b
Формулы сокращенного умножения a b Знакомство с линейкой, единицей измерения длины – сантиметр (2 урок)
Знакомство с линейкой, единицей измерения длины – сантиметр (2 урок) Дискретные случайные величины
Дискретные случайные величины Применение математики в нематематических областях
Применение математики в нематематических областях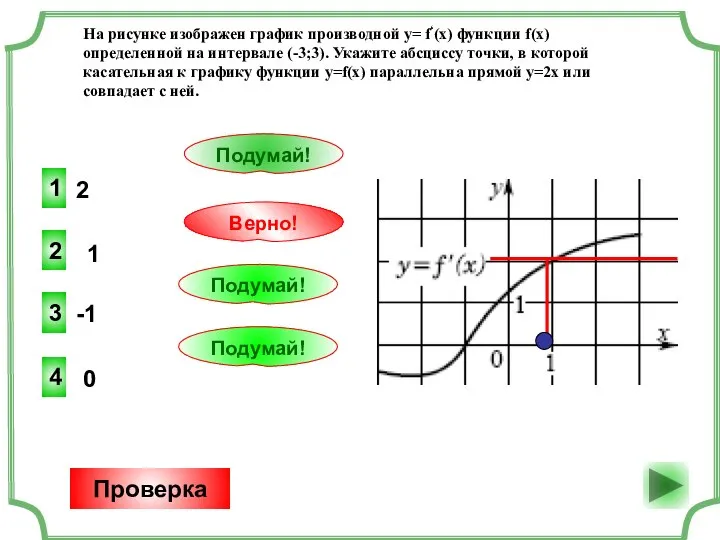 Решение задач
Решение задач Линейная функция и ее график
Линейная функция и ее график Математика (1 класс)
Математика (1 класс) Методы кластеризации
Методы кластеризации Презентация на тему Русская система мер
Презентация на тему Русская система мер