Содержание
- 2. Производная Большинство функций, изучаемых в школьном курсе алгебры и начал анализа, имеют себе в пару другую
- 3. Задача На станции метро расстояние от тормозной отметки до остановки первого вагона равно 80 м. С
- 4. Решение Ѵ-?(мгновенная скорость в этот момент времени) Тормозной путь Где а- ускорение, t-время торможения. S=80, a=1,6,
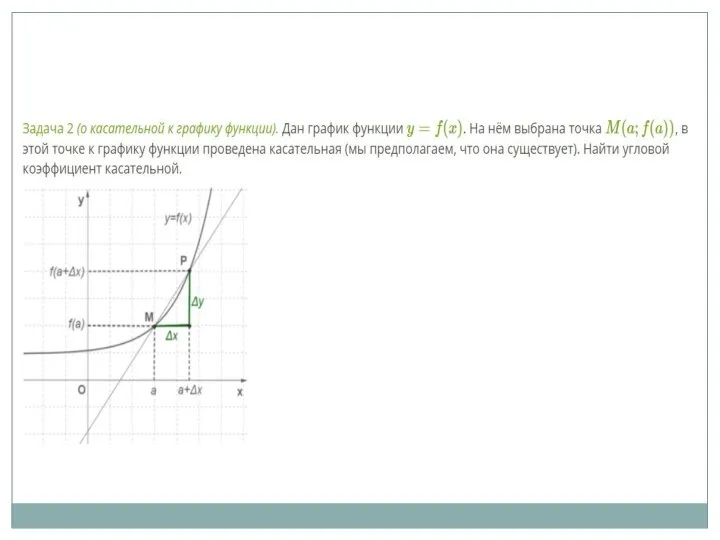
- 5. Задачи, приводящие к понятию производной
- 17. Таблица производных
- 18. Таблица производных
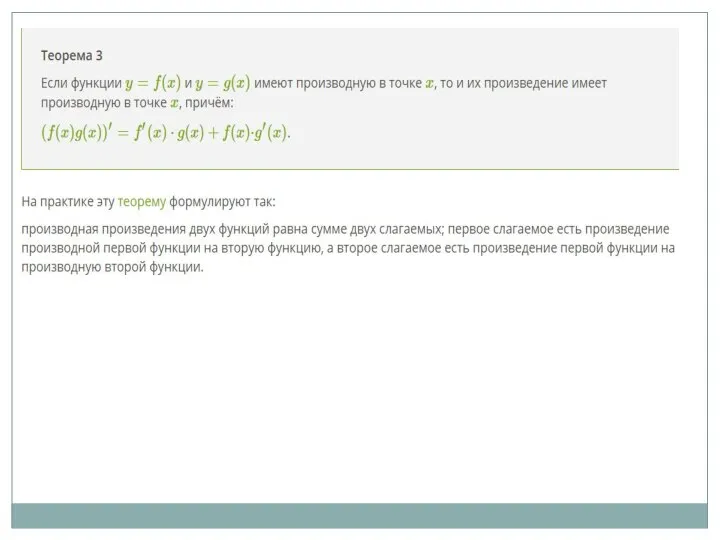
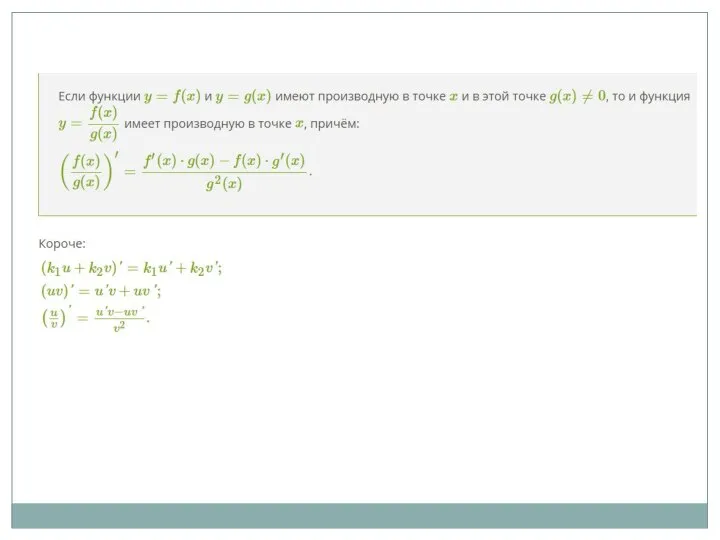
- 19. Правила дифференцирования
- 23. Правила дифференцирования Формулами дифференцирования обычно называют формулы для нахождения производных конкретных функций, например:
- 24. Формулы дифференцирования
- 25. Найти производную функции Решение
- 26. Решение Найти производную функции
- 27. Решение Найти производную функции
- 28. Решение Найти производную функции
- 29. Решение Найти производную функции
- 30. Понятие и вычисление производной n-го порядка
- 32. Производная сложной функции
- 35. Производная сложной функции Пример Решение
- 36. Решение Производная сложной функции
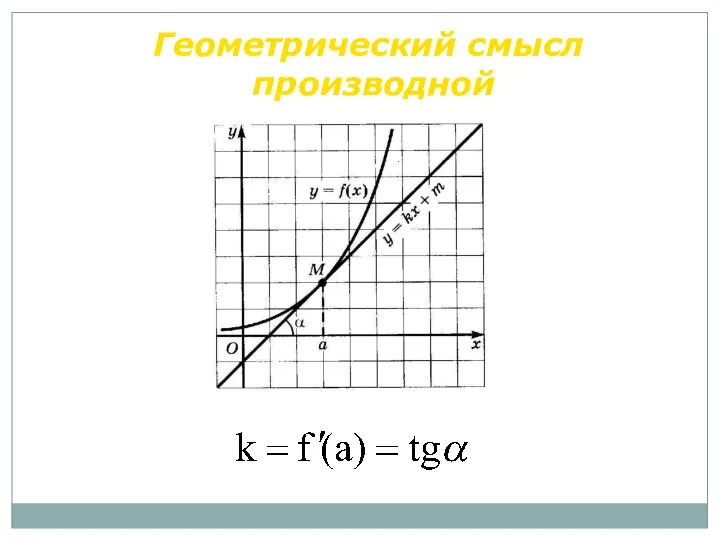
- 37. Геометрический смысл производной
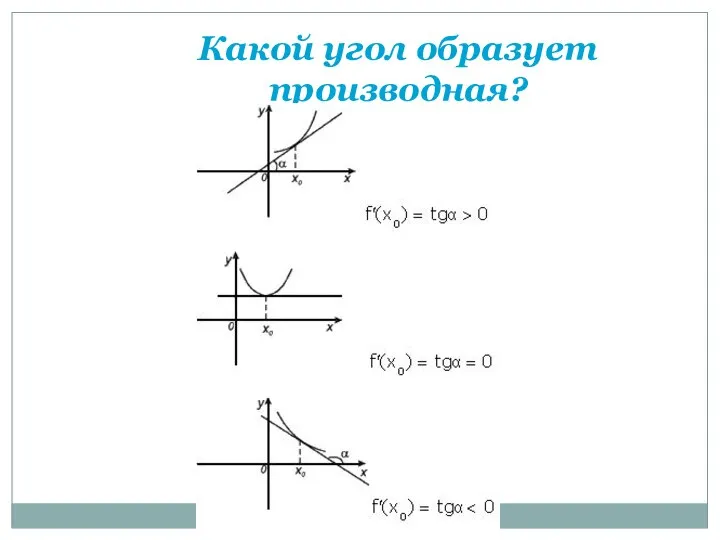
- 38. Какой угол образует производная?
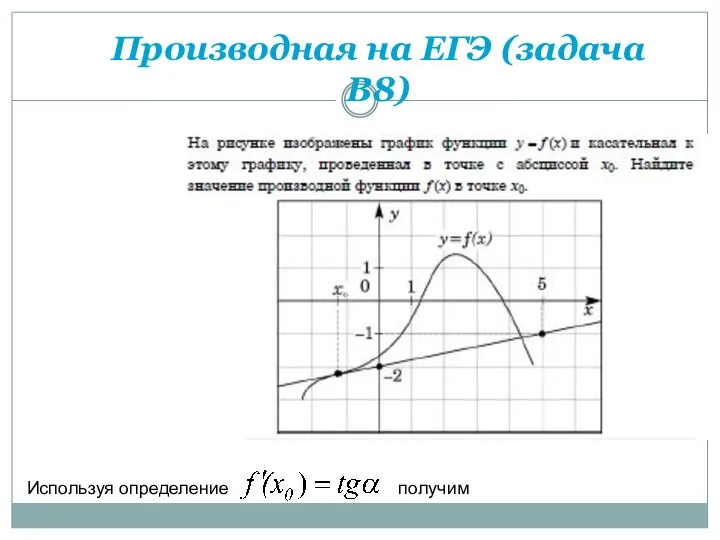
- 39. Производная на ЕГЭ (задача В8) Используя определение получим
- 40. Производная на ЕГЭ (задача В8) На рисунке изображены график функции y = f(x) и касательная к
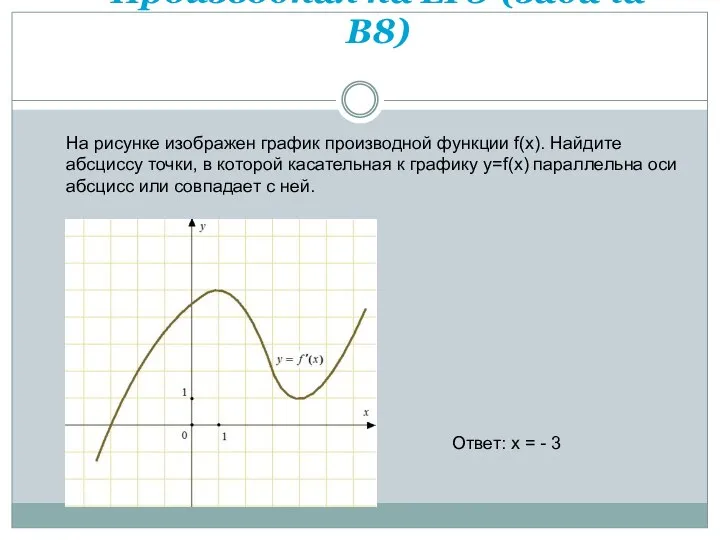
- 41. Производная на ЕГЭ (задача В8) На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в
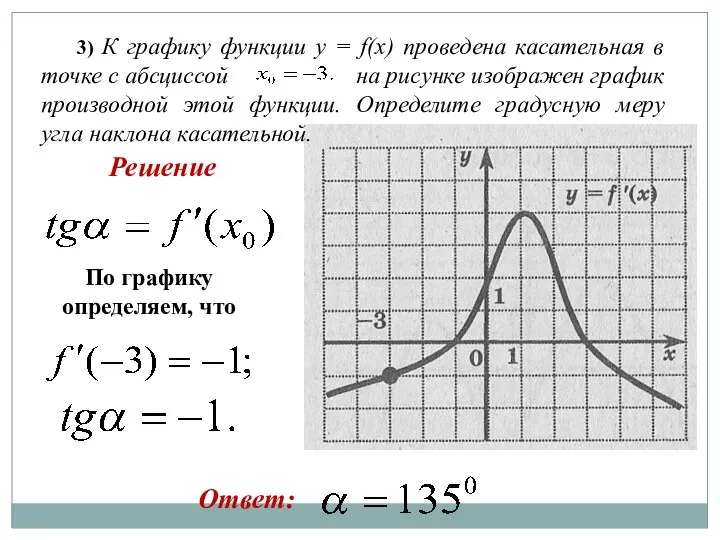
- 42. 3) К графику функции y = f(x) проведена касательная в точке с абсциссой на рисунке изображен
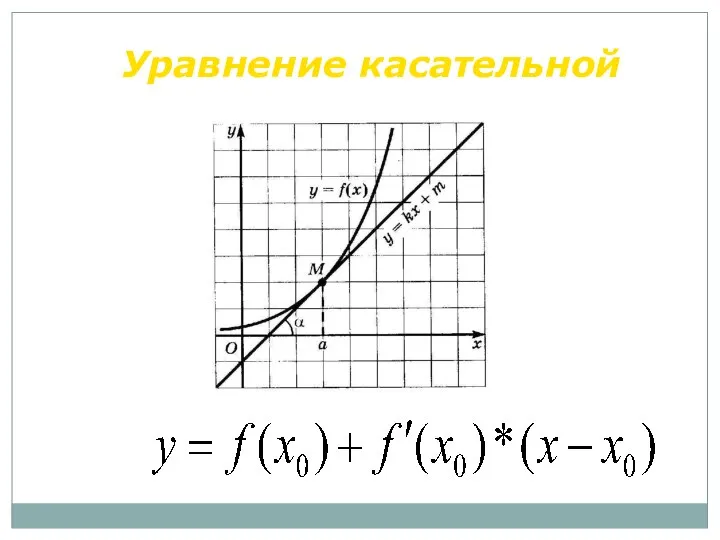
- 43. Уравнение касательной
- 44. Пример Составить уравнение касательной, проведенной к графику функции точке графика с абсциссой Решение Ответ:
- 45. Физический (механический) смысл производной
- 46. Пример Материальная точка движется по прямой так, что ее скорость в момент времени t равна Найдите
- 48. Скачать презентацию




































 Числа от 1 до 100. Умножение и деление. Закрепление
Числа от 1 до 100. Умножение и деление. Закрепление Экономическая статистика. Демография предприятий
Экономическая статистика. Демография предприятий Презентация на тему Множества
Презентация на тему Множества  Признаки равенства треугольников
Признаки равенства треугольников Метод искусственного базиса
Метод искусственного базиса Презентация на тему ТАКИЕ РАЗНЫЕ ЧИСЛА
Презентация на тему ТАКИЕ РАЗНЫЕ ЧИСЛА  Станция Игровая. Занимательная математика
Станция Игровая. Занимательная математика Линейное уравнение с двумя переменными
Линейное уравнение с двумя переменными Решение уравнений
Решение уравнений Отрезок
Отрезок Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Презентация на тему Случайные события и вероятность
Презентация на тему Случайные события и вероятность  Комбинаторика. Правило умножения
Комбинаторика. Правило умножения Показательная, степенная и логарифмическая функции их свойства и графики
Показательная, степенная и логарифмическая функции их свойства и графики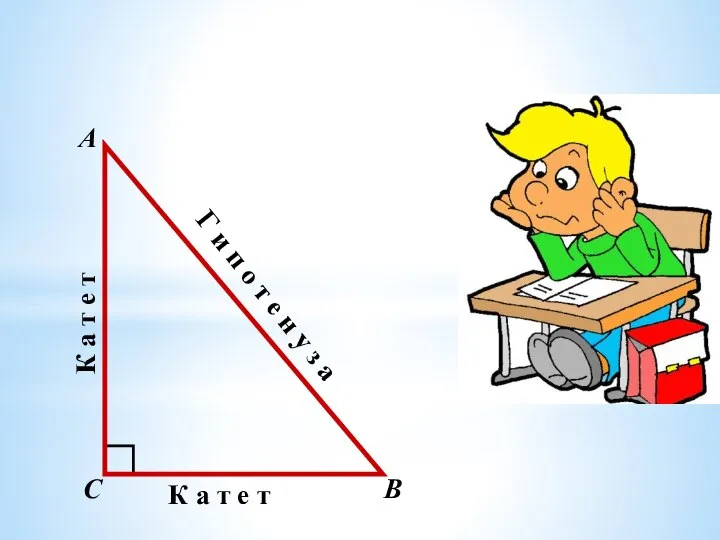 Гипотенуза и катеты в треугольнике. Задачи
Гипотенуза и катеты в треугольнике. Задачи Zaokrugljivanje decimalnih brojeva
Zaokrugljivanje decimalnih brojeva 29.09 Решение задач
29.09 Решение задач Свойства арифметического корня
Свойства арифметического корня Статистический образ мышления. Научная публикация. (Лекция 3)
Статистический образ мышления. Научная публикация. (Лекция 3) Эконометрика
Эконометрика Геометрическая прогрессия. Задачи в формате экзамена
Геометрическая прогрессия. Задачи в формате экзамена Перпендикуляр и наклонная к прямой
Перпендикуляр и наклонная к прямой Письмо цифр
Письмо цифр Дискретная математика: теория алгоритмов и сложность вычислений
Дискретная математика: теория алгоритмов и сложность вычислений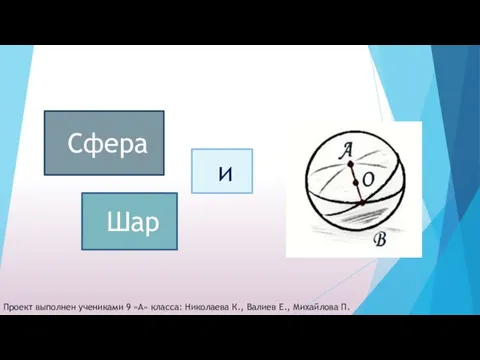 Сфера и шар
Сфера и шар Кубический корень
Кубический корень Решение неравенств методом интервалов
Решение неравенств методом интервалов Золотое сечение. 9 класс
Золотое сечение. 9 класс