Содержание
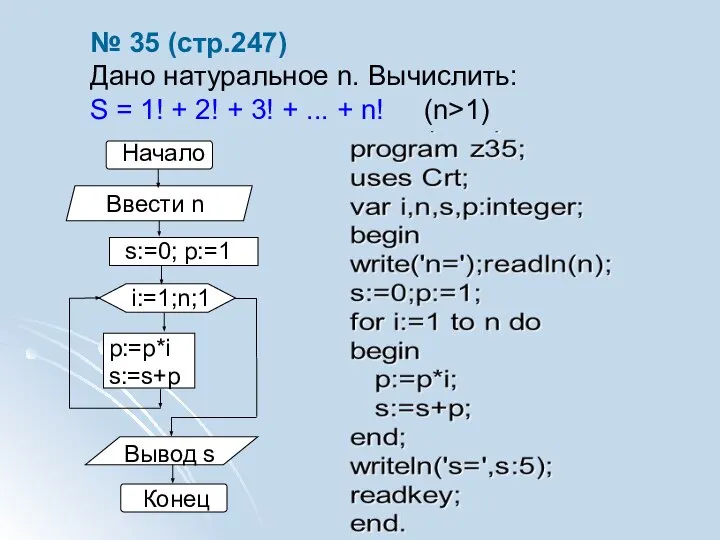
- 2. № 35 (стр.247) Дано натуральное n. Вычислить: S = 1! + 2! + 3! + ...
- 3. № 36 (стр.247) Дано натуральное n. Вычислить: Начало i=1;n;1 Вывод S Конец s:=0 s:=s+1/sqr(2*i+1) Ввести n
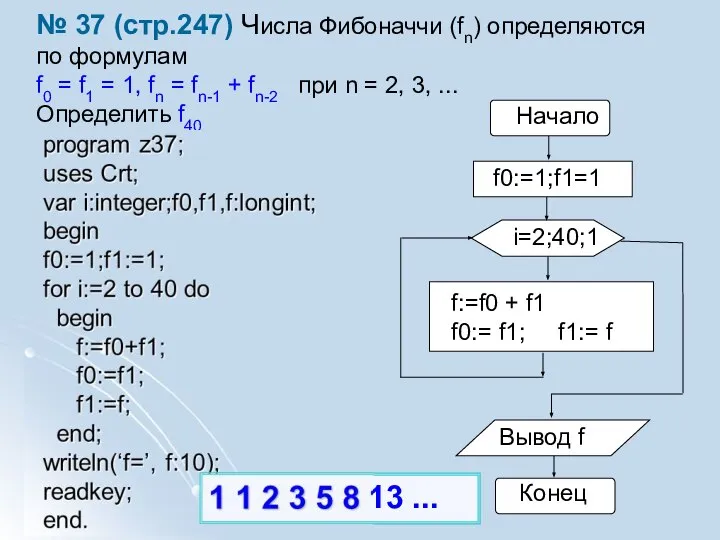
- 4. № 37 (стр.247) Числа Фибоначчи (fn) определяются по формулам f0 = f1 = 1, fn =
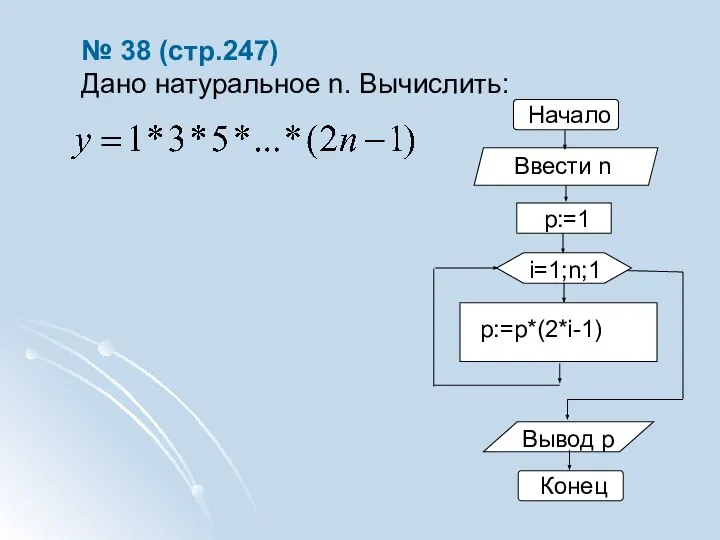
- 5. № 38 (стр.247) Дано натуральное n. Вычислить: Начало i=1;n;1 Вывод p Конец p:=1 p:=p*(2*i-1) Ввести n
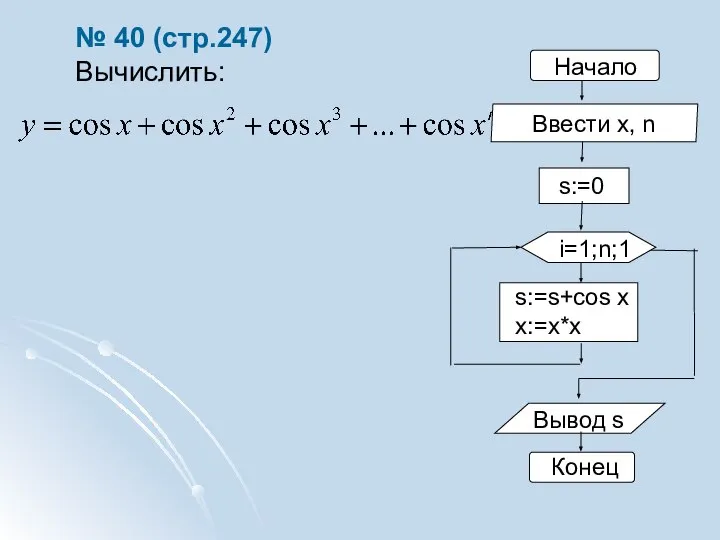
- 6. № 40 (стр.247) Вычислить: Начало Вывод s Конец s:=0 s:=s+cos x x:=x*x Ввести x, n i=1;n;1
- 8. Скачать презентацию

 Призма. Построение сечений призмы плоскостями
Призма. Построение сечений призмы плоскостями Деление дробей
Деление дробей Системы уравнений. Основные способы их решения. 9 класс
Системы уравнений. Основные способы их решения. 9 класс Координатная плоскость
Координатная плоскость Приемы решения целых уравнений
Приемы решения целых уравнений Решение задач. Повторение пройденного
Решение задач. Повторение пройденного Решение задач с помощью пропорции. 5 класс
Решение задач с помощью пропорции. 5 класс Линейная алгебра и аналитическая геометрия
Линейная алгебра и аналитическая геометрия Числовые промежутки
Числовые промежутки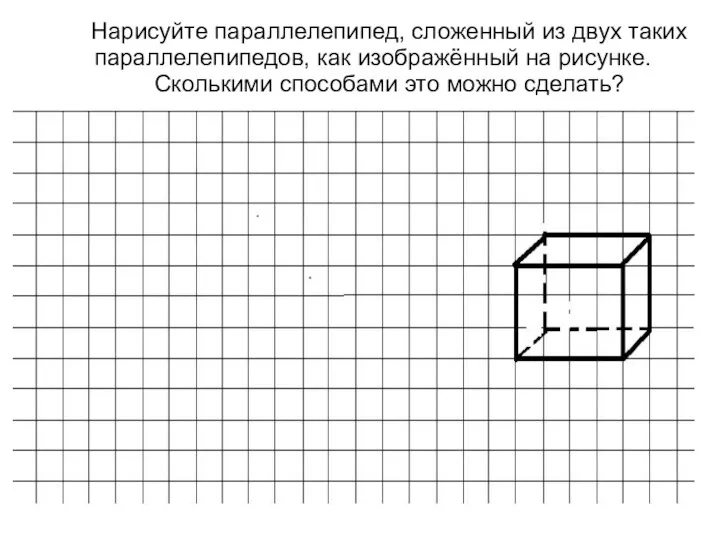 Многогранники. 5 класс
Многогранники. 5 класс Случаи вычитания 12 -
Случаи вычитания 12 - Хитрые задачи. 4 класс
Хитрые задачи. 4 класс Состав числа 7
Состав числа 7 Логарифмические уравнения и их системы
Логарифмические уравнения и их системы Вопросы при решении задач
Вопросы при решении задач Разбор и решение задания ОГЭ по математике
Разбор и решение задания ОГЭ по математике Математическое лото. Дидактическая настольно-печатная игра
Математическое лото. Дидактическая настольно-печатная игра СРС 2 ВСК 2. Задачи
СРС 2 ВСК 2. Задачи Задачи на увеличение (уменьшение) числа на несколько единиц
Задачи на увеличение (уменьшение) числа на несколько единиц Преобразование графиков
Преобразование графиков Презентация на тему Деление с остатком
Презентация на тему Деление с остатком  Координатная плоскость 6 класс - Презентация по математике_
Координатная плоскость 6 класс - Презентация по математике_ Решение задач на вычисление площадей фигур
Решение задач на вычисление площадей фигур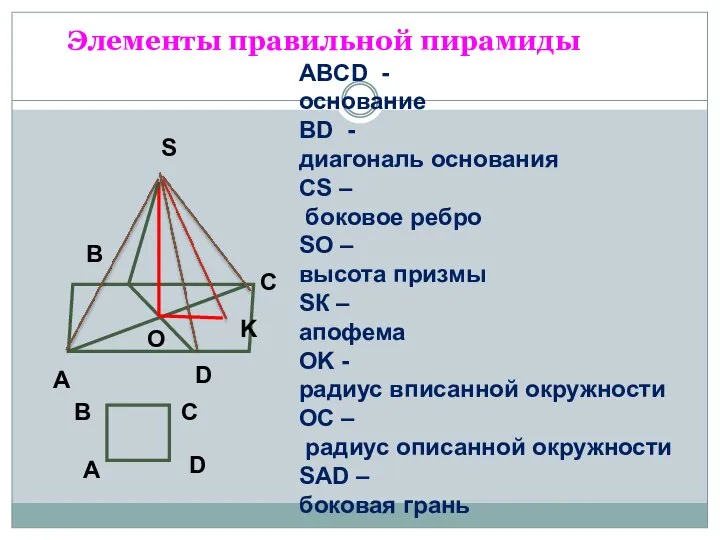 Правильная пирамида
Правильная пирамида Координаты на прямой
Координаты на прямой Решение логарифмических уравнений
Решение логарифмических уравнений Задачи с экономическим содержанием. Часть 1
Задачи с экономическим содержанием. Часть 1 Средняя линия треугольника
Средняя линия треугольника