Пропорциональные отрезки в прямоугольном треугольнике

Ученик, который учится без желания, подобен птице без крыльев.
Саади
персидский мыслитель и писатель, 13 в.н.э.

Задание :
в прямоугольном треугольнике
отыскать пропорциональные отрезки
и раскрыть некоторые его важные свойства

Верно ли утверждение:
два любых прямоугольных треугольника – подобны
?

Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет
треугольник на два подобных
треугольника, каждый из которых подобен данному.
Свойство прямоугольного треугольника.

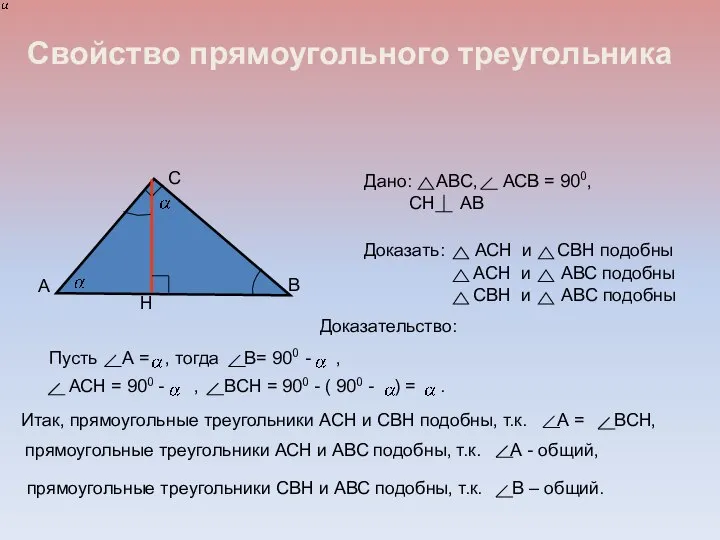
Свойство прямоугольного треугольника
Доказательство:

Определение.
Отрезок XY называется средним геометрическим (или средним пропорциональным) между отрезками АВ и CD, если
а).Найдите среднее пропорциональное отрезков MN и KP, если MN=4, KP=25

б). Найдите длину отрезка AB, если среднее пропорциональное отрезков AB и СD равно 90см и CD=100 см

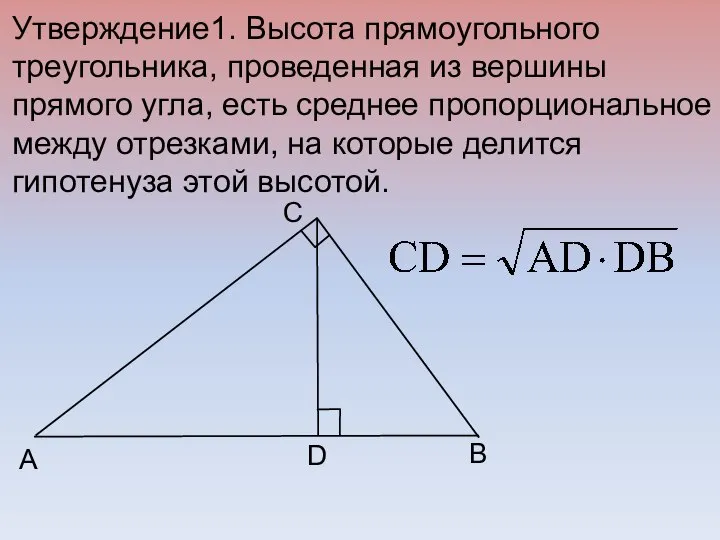
B
C
A
D
Утверждение1. Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.

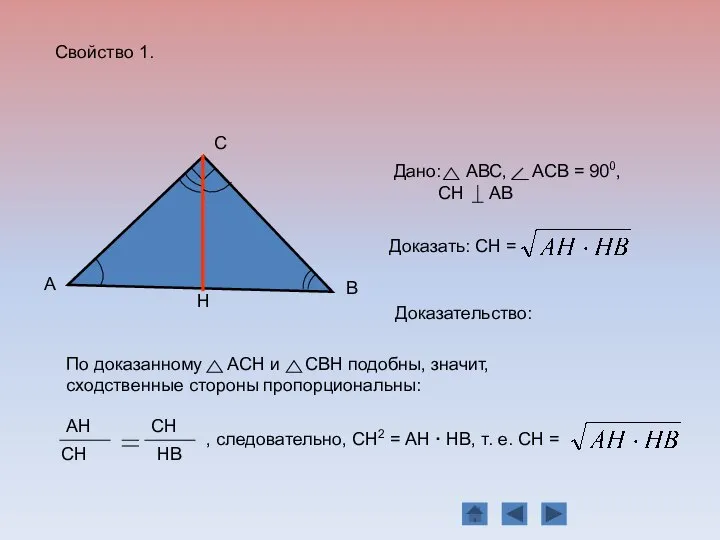
Свойство 1.
Доказательство:

·

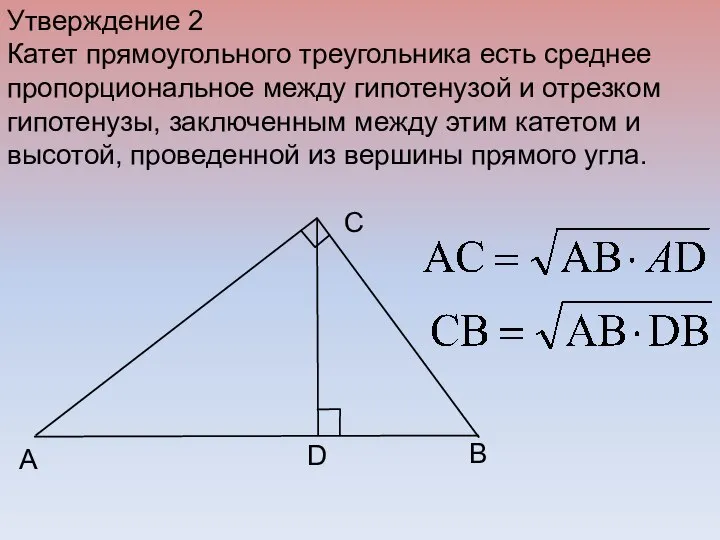
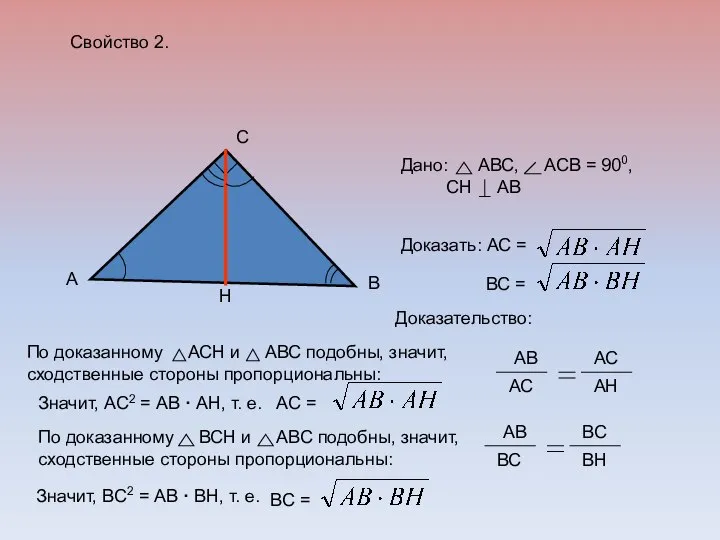
B
C
A
D
Утверждение 2
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между этим катетом и высотой, проведенной из вершины прямого угла.

Свойство 2.
Доказательство:

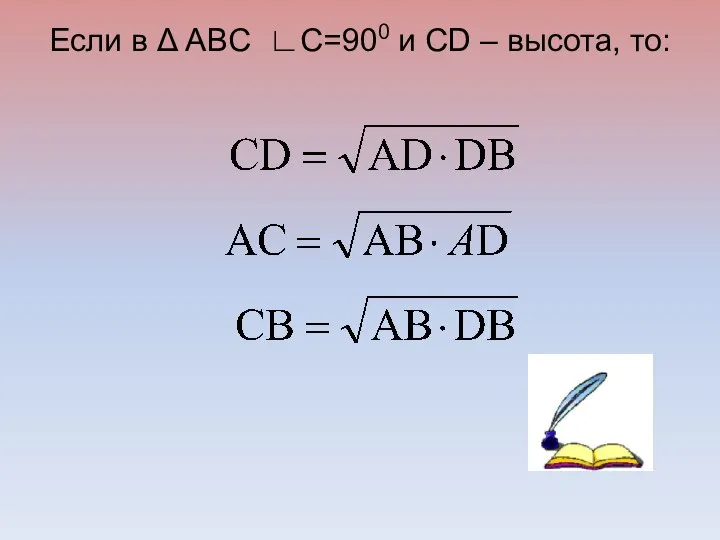
Если в Δ ABC ∟С=900 и CD – высота, то:

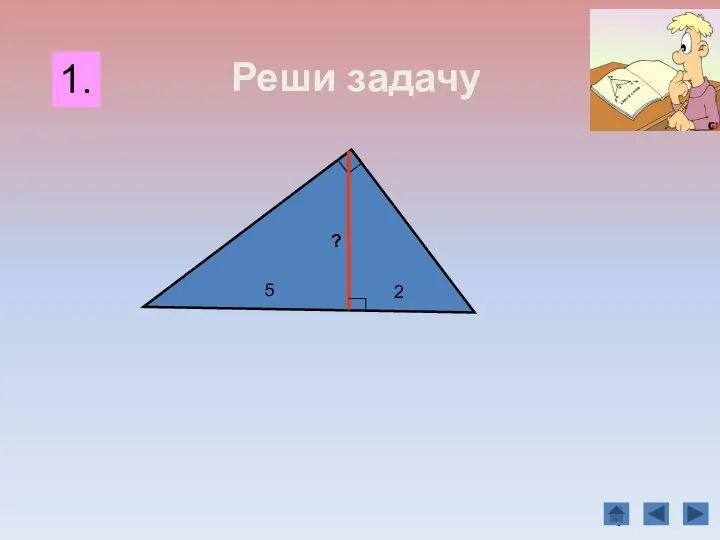
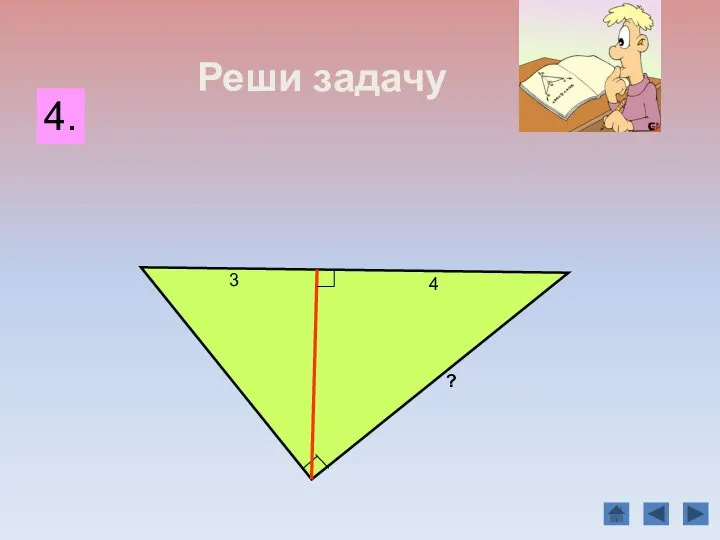
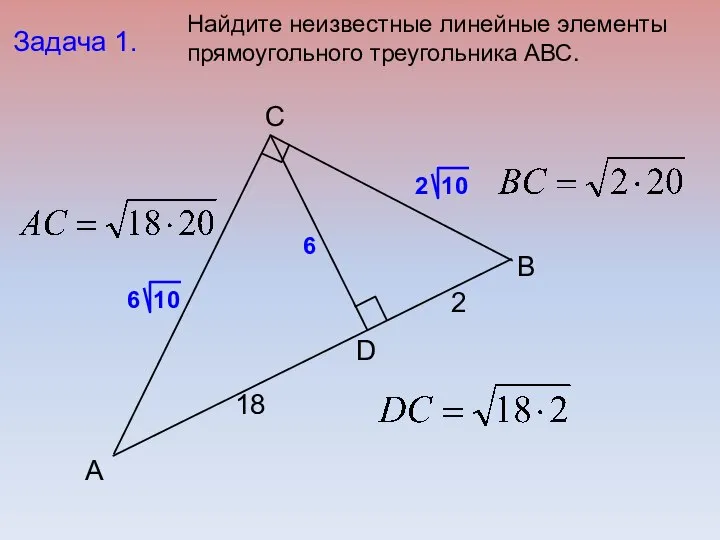
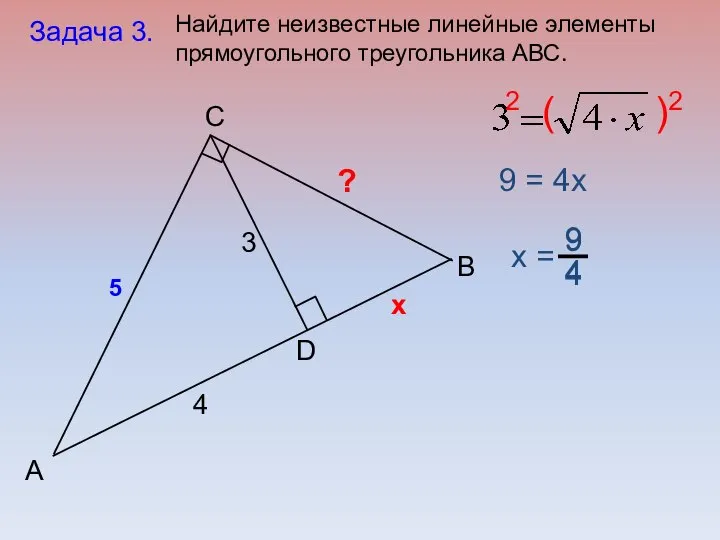
B
C
А
D
Задача 1.
18
2
6
Найдите неизвестные линейные элементы прямоугольного треугольника АВС.

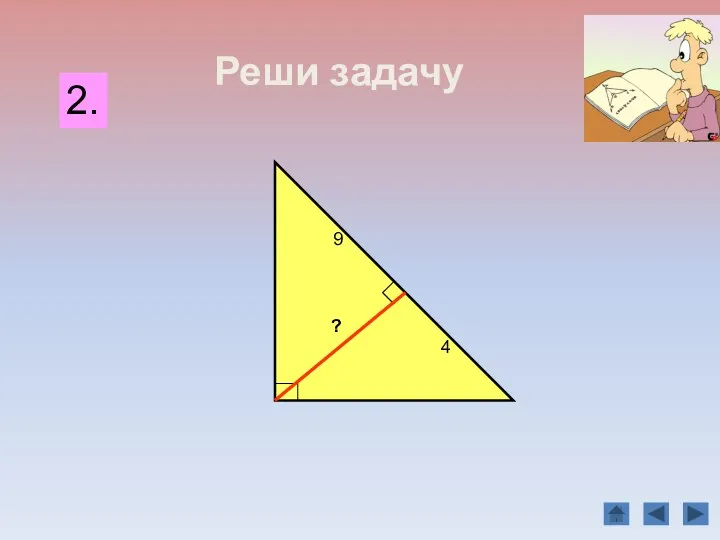
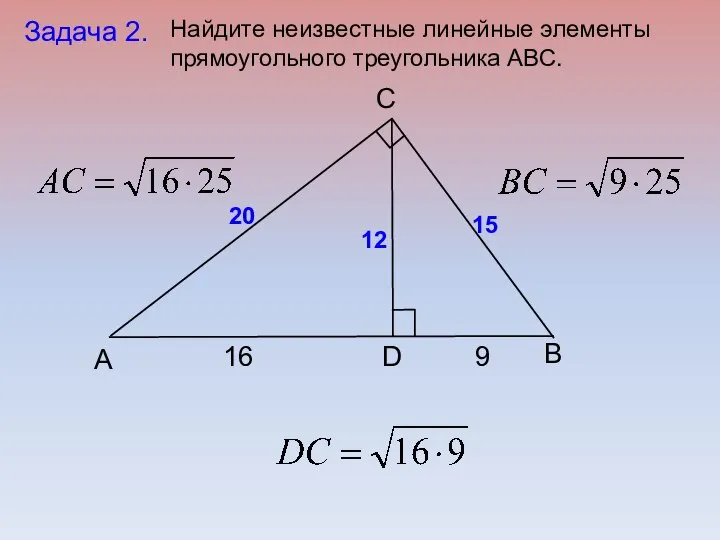
B
C
А
D
Задача 2.
16
9
20
15
12
Найдите неизвестные линейные элементы прямоугольного треугольника АВС.

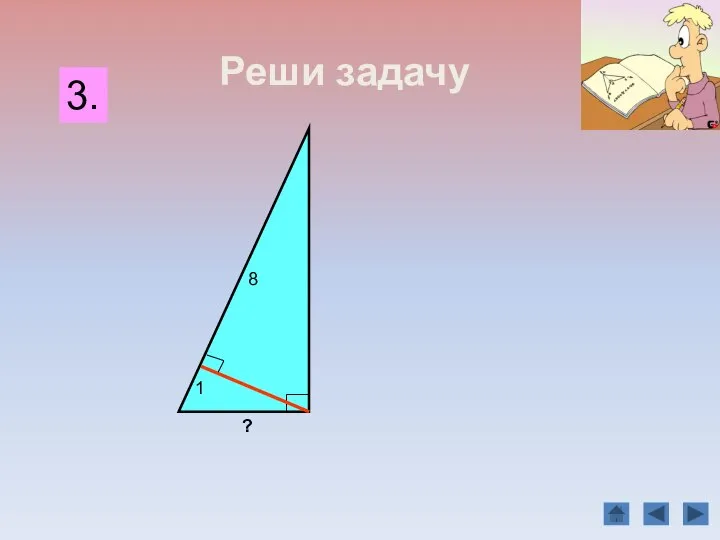
B
C
А
D
3
4
5
Найдите неизвестные линейные элементы прямоугольного треугольника АВС.
х
2 ( )2
9 = 4х
?
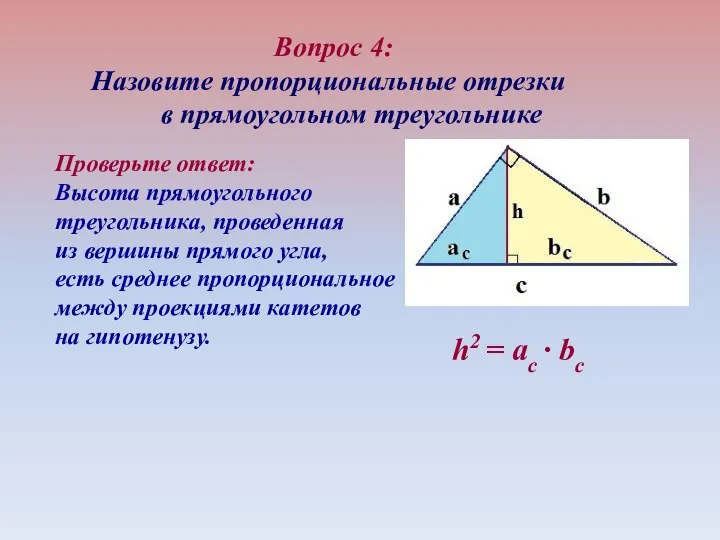
Задача 3.

Вопрос 4:
Назовите пропорциональные отрезки
в прямоугольном треугольнике
h2 = ac ∙ bc
Проверьте ответ:
Высота прямоугольного треугольника, проведенная
из вершины прямого угла,
есть среднее пропорциональное
между проекциями катетов
на гипотенузу.

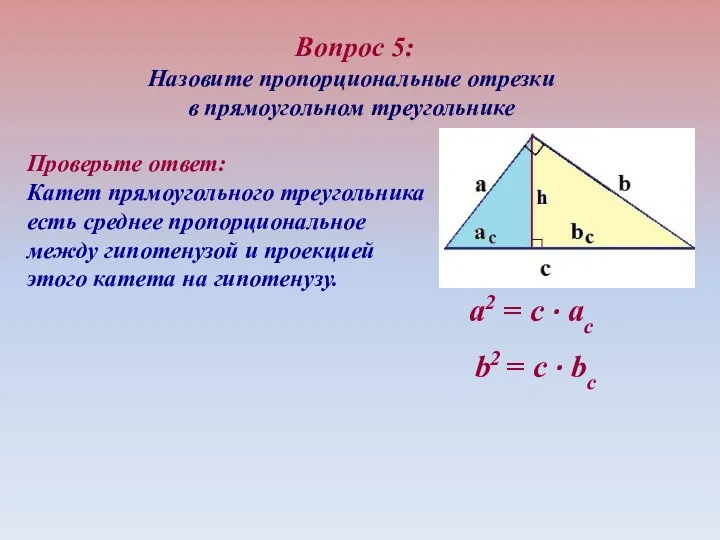
Вопрос 5:
Назовите пропорциональные отрезки
в прямоугольном треугольнике
а2 = c ∙ aс
b2 = c ∙ bс
Проверьте ответ:
Катет прямоугольного треугольника
есть среднее пропорциональное
между гипотенузой и проекцией
этого катета на гипотенузу.

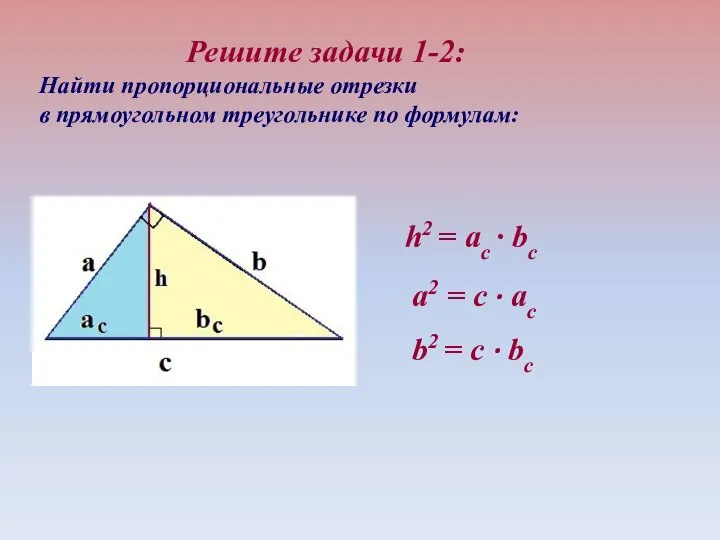
Решите задачи 1-2:
Найти пропорциональные отрезки
в прямоугольном треугольнике по формулам:
а2 = c ∙ aс
b2 = c ∙ bс
h2 = ac ∙ bc

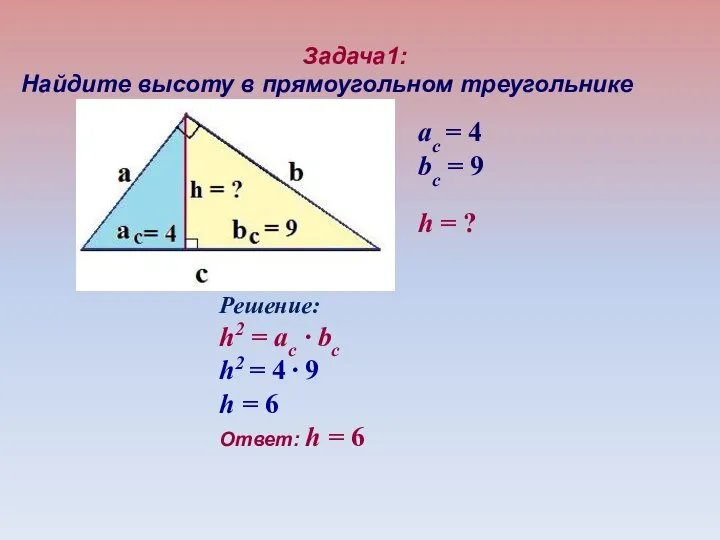
Задача1:
Найдите высоту в прямоугольном треугольнике
aс = 4
bс = 9
Решение:
h2 = ac ∙ bc
h2 = 4 ∙ 9
h = 6
Ответ: h = 6
h = ?

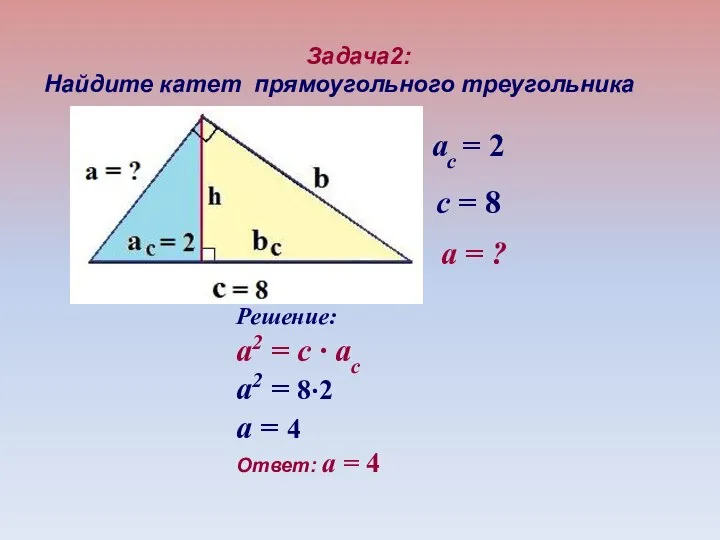
Задача2:
Найдите катет прямоугольного треугольника
а = ?
c = 8
ac = 2
Решение:
a2 = c ∙ ac
a2 = 8∙2
a = 4
Ответ: a = 4