Проверка статистических гипотез

Практическая работа №3

Основные понятия
Статистическая гипотеза – это предположение о значении параметров закона распределения с.в. Х (параметрическая) или его виде (непараметрическая).
Статистическая гипотеза называется простой, если она однозначно определяет распределение с.в. Х; в противном случае, гипотеза называется сложной.

Основные понятия
Проверяемую гипотезу обычно называют нулевой (или основной) и обозначают Н0.
Наряду с нулевой гипотезой рассматривают альтернативную (или конкурирующую) гипотезу Н1, являющуюся логическим отрицанием Н0.
Выбор альтернативной гипотезы определяется конкретной формулировкой задачи.
Проверка статистической гипотезы H состоит в выяснении того, насколько эта гипотеза согласуется с опытными данными X.

Основные понятия
Решение – принять или отвергнуть гипотезу Н0 – принимается на основании некоторого правила или критерия по выборочным данным. При этом выбирается подходящая функция элементов выборки, или статистика критерия, которую в общем случае будем обозначать Z.
Правило, по которому принимается решение принять или отклонить гипотезу Н0, называется критерием К.
Принцип проверки статистических гипотез: маловероятные события считаются невозможными, а события, имеющие большую вероятность – достоверными.

Принцип проверки статистических гипотез
Реализация принципа:
Задать уровень значимости α.
Выбрать статистику Z критерия К;
Множество значений статистики Z разбить на непересекающиеся подмножества – критическую область и область принятия гипотезы Н0.

Критическая область
Множество значений статистики Z, при которых принимается решение отклонить гипотезу Н0, называется критической областью.
Графически эта область определяется по кривой распределения.
Уровень значимости α определяет «размер» критической области
Критическая область выбирается так, чтобы вероятность попадания в нее была минимальной (равной α), если верна нулевая гипотеза Н0, и максимальной в противоположном случае.

Критическая область
В зависимости от вида конкурирующей гипотезы и распределения критерия выбирают вид расположения критической области: правосторонняя, левосторонняя или двусторонняя.
Границы (критические точки) при заданном уровне значимости находят из соотношений для критических областей:
правосторонней: P(Z > Zкр) = α;
левосторонней: P(Z < Zкр) = α;
двусторонней: P(Z < Zкр) = α /2 и P(Z > Zкр) = α /2.

Область принятия решения
Множество значений статистики Z, при которых гипотеза Н0 принимается, называется областью принятия решения.

Критерий, основанный на использовании заранее заданного уровня значимости α, называют критерием значимости.
Проверка статистических гипотез может быть проведена на основе соответствующих доверительных интервалов.

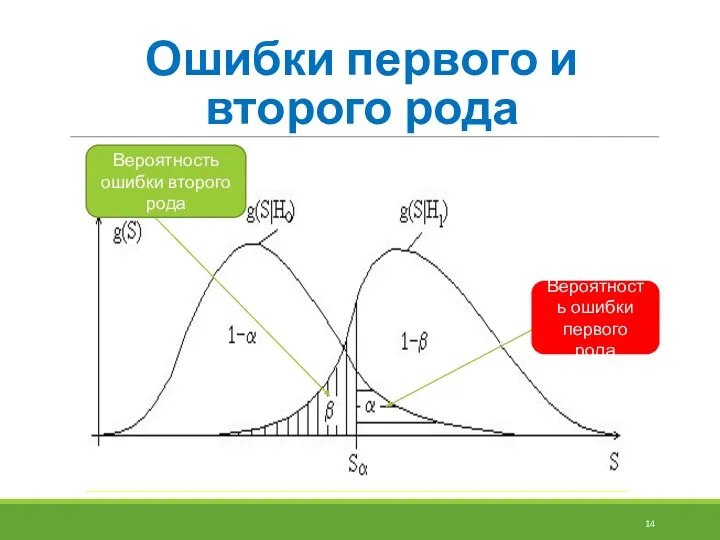
Ошибки первого и второго рода
Уровень значимости α – это вероятность ошибки первого рода, т.е. вероятность того, что будет отвергнута гипотеза Н0, если на самом деле для генеральной совокупности верна гипотеза Н0.
Значение α устанавливается на основе практического опыта в различных областях исследования. Вероятность α задается заранее малым числом: 0,05; 0,01; 0,005; 0,001.
Вероятность ошибки второго рода обозначают β – это вероятность того, что будет принята гипотеза Н0, если на самом деле верна гипотеза Н1.
Вероятность не совершить ошибку второго рода (1 – β), т. е. вероятность правильного отклонения неверной нулевой гипотезы, называют мощностью критерия.

Ошибки первого и второго рода

Ошибки первого и второго рода
Статистическая ошибка первого рода (Type I Error) – ошибка обнаружить различия или связи, которые на самом деле не существуют!
Статистическая ошибка второго рода (Type II Error) - не обнаружить различия или связи, которые на самом деле существуют
«Судебная» аналогия: Вердикт «Не виновен» или «Виновен»
Ошибка первого рода - невинный обвинен
Ошибка второго рода - виновный освобожден

Ошибки первого и второго рода
Вероятность ошибки первого рода
Вероятность ошибки второго рода

Этапы проверки гипотезы о параметрах распределения
1. формулируются гипотезы Н0 и Н1;
2. задается уровень значимости α;
3. выбирается статистика Z критерия для проверки Н0; определяется выборочное распределение статистики Z при условии, что верна Н0;
4. в зависимости от Н1 определяется критическая область;
5. вычисляется выборочное значение статистики z;
6. принимается статистическое решение.

Статистическое решение

Замечания
1. На этапах 4-7 используют статистику, квантили которой табулированы.
2. В статистических пакетах обычно не используется значения задаваемого уровня значимости. В выходных данных содержатся выборочные значения статистики критерия и вероятность того, что с.в. превышает выборочное значение.
Эта вероятность называется р-значением (p-level).

Пример 1
Сб. задач по математике для втузов. Ч. 3. Теория вероятностей и математическая статистика / под ред. А.В. Ефимова.
По паспортным данным автомобильного двигателя расход топлива на 100 км. пробега составляет 10л. В результате изменения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки проводятся испытания 25 случайно отобранных автомобилей с модернизированным двигателем, причем выборочное среднее расходов топлива на 100 км. пробега по результатам испытаний составило 9,3 л. Предположим, что выборка расходов топлива получена из нормально распределенной генеральной совокупности со средним а и дисперсией 4 л2 . Используя критерий значимости, проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.

Пример 2

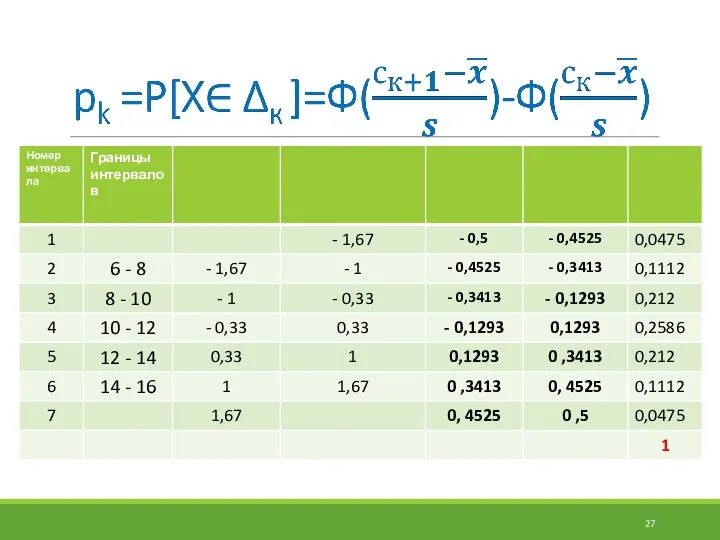
Критерии согласия

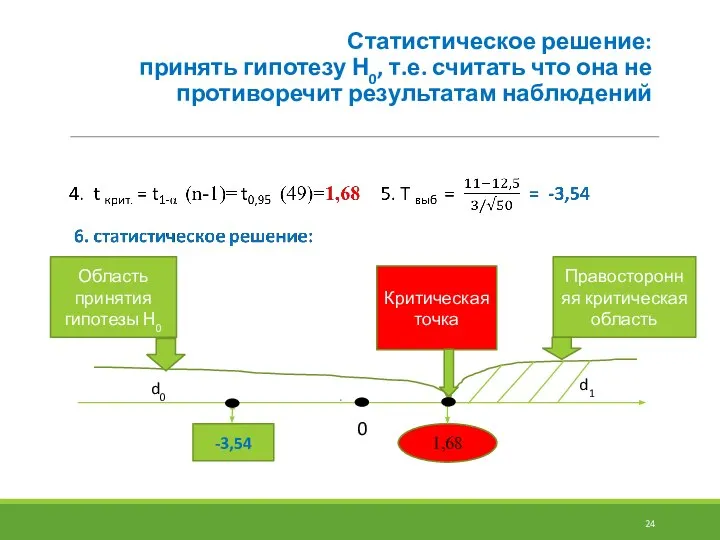
Статистическое решение:
принять гипотезу Н0, т.е. считать что она не противоречит результатам наблюдений
1,68
-3,54
Область принятия гипотезы Н0
Критическая точка
Правосторонняя критическая область
d1
d0
0

32,4
71,4
d0
d1
d1
Статистическое решение:
принять гипотезу Н0, т.е. считать что она не противоречит результатам наблюдений

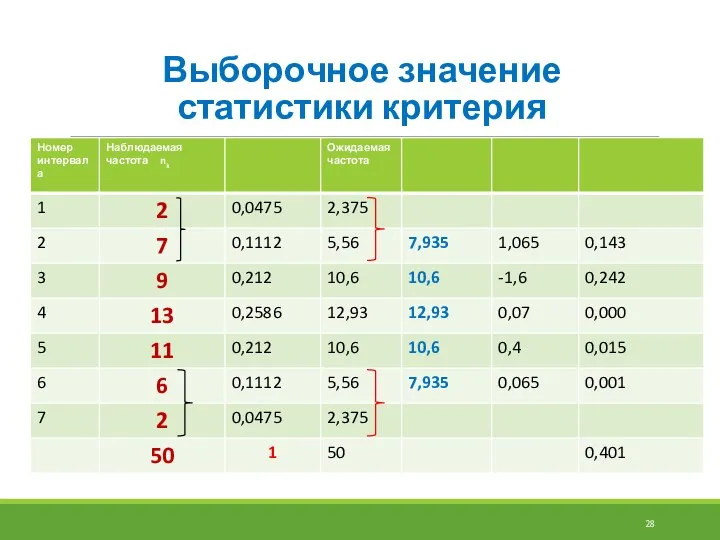
Выборочное значение статистики критерия