Прямоугольные треугольники

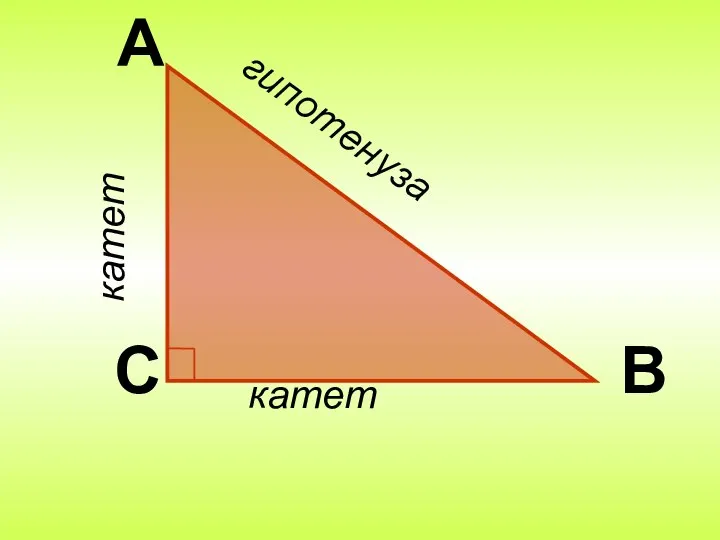
А
С
В
гипотенуза
катет
катет

Предполагаемые гипотезы
Сумма острых углов прямоугольного треугольника равна 900.
Катет прямоугольного треугольника, лежащий против угла в 300, равен половине гипотенузы.
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 300.

Сумма двух острых углов прямоугольного треугольника равна 90°.
Доказательство:
Сумма углов треугольника равна 180° , а прямой угол равен 90° , поэтому сумма двух острых углов прямоугольного треугольника равна 90° .
Свойство 1

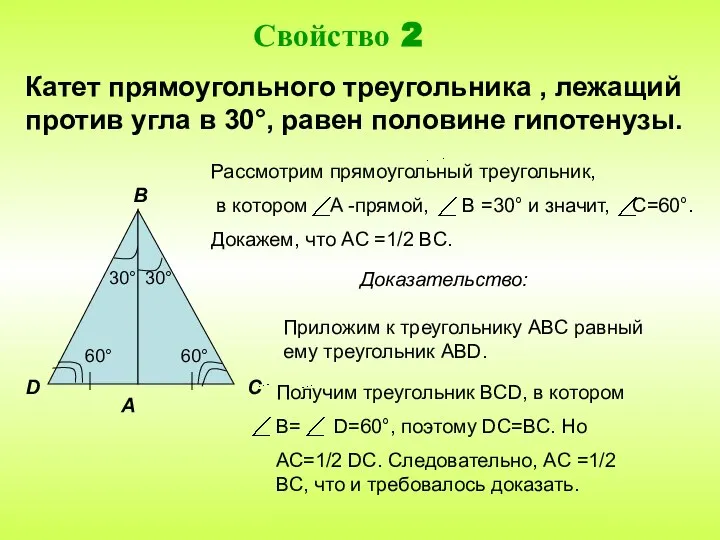
Катет прямоугольного треугольника , лежащий против угла в 30°, равен половине гипотенузы.
Доказательство:
Приложим к треугольнику АВС равный ему треугольник АВD.
Рассмотрим прямоугольный треугольник,
в котором A -прямой, B =30° и значит, C=60°.
Докажем, что AC =1/2 BC.
Получим треугольник ВСD, в котором
В= D=60°, поэтому DС=ВС. Но
АС=1/2 DС. Следовательно, AC =1/2 BC, что и требовалось доказать.
Свойство 2

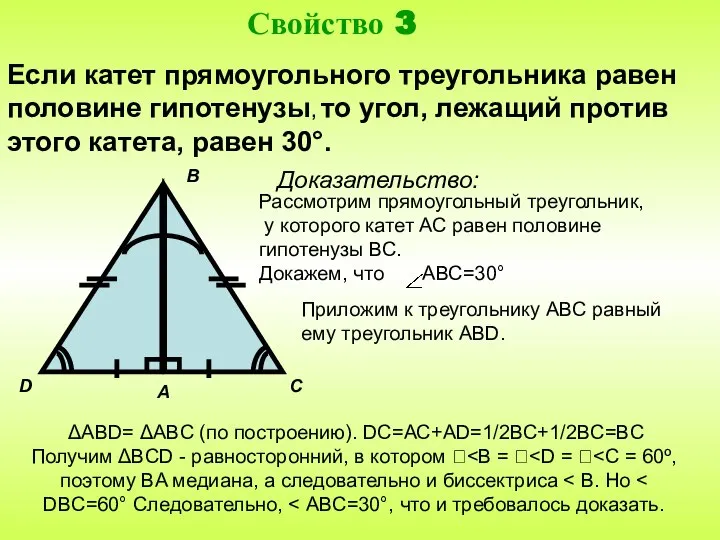
Доказательство:
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
Приложим к треугольнику АВС равный ему треугольник АВD.
Свойство 3
ΔАВD= ΔАBС (по построению). DC=АС+AD=1/2BC+1/2BC=BC Получим ΔBСD - равносторонний, в котором 

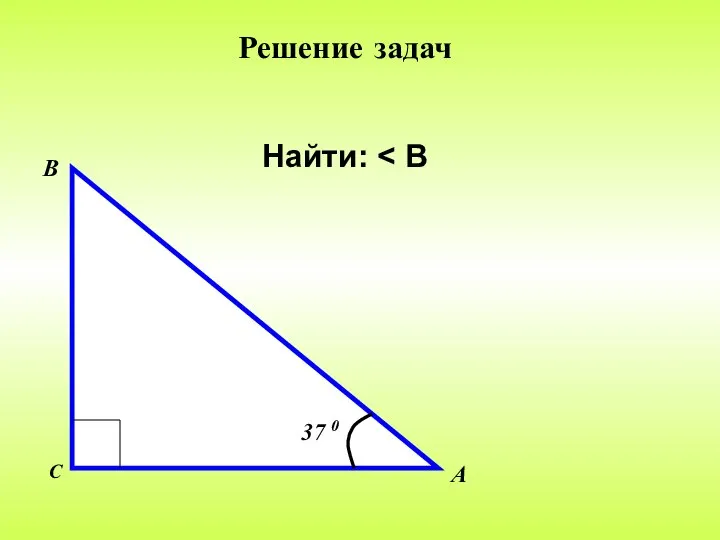
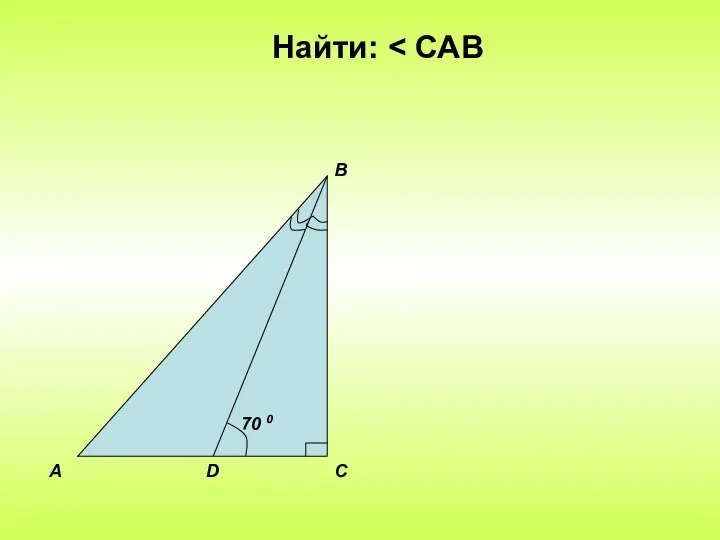
Решение задач
Найти: < В

Найти: < САВ