Классическое определение вероятности

Основные понятия теории вероятности
Наблюдением или опытом называют реализацию определенных условий, в которых событие может состояться.
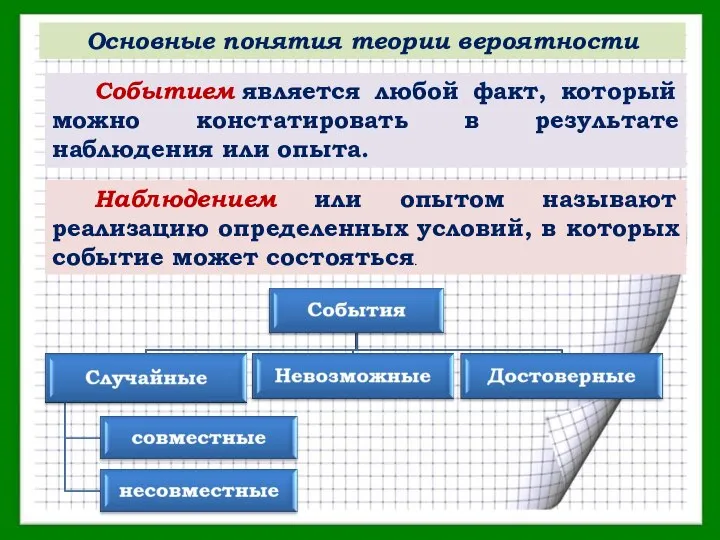
Событием является любой факт, который можно констатировать в результате наблюдения или опыта.

Если полное множество событий состоит только из двух несовместных событий, то их называют взаимно противоположными или альтернативными событиями.
События называют равновозможными, если ни у одного из них нет объективных преимуществ.
При классическом определении вероятность события определяется равенством:
Р (А) = m / n,
где m – число элементарных исходов испытания, благоприятствующих появлению события А;
n - общее число возможных элементарных исходов испытания.

Пример 1. Найти вероятность того, что при бросании трех игральных костей шестерка выпадет на одной (безразлично какой) кости, если на гранях двух других костей выпадут числа очков, не совпадающие между собой и не равные шестерке.
Пример 2. В ящике 10 одинаковых деталей, помеченных номерами 1, 2 , …, 10. Наудачу извлечены шесть деталей. Найти вероятность того, что среди извлеченных деталей окажутся: а) деталь № 1; б) детали № 1 и № 2.
Пример 3. В цехе работают шесть мужчин и четыре женщины. По табельным номерам наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины.

Свойства вероятностей
Свойство 1. Если можно вычислить возможности возникновения события А и их число совпадает общим с числом равновозможных событий, то вероятность события А равна 1.
Свойство 2. Вероятность невозможного события равна 0. Если число возможностей события А равна 0, то и
Свойство 3. Вероятность случайного события всегда больше 0 и меньше 1:
или

Статистическая вероятность
Относительной частотой события А называют отношение числа наблюдений, в которых наблюдается А, к числу всех наблюдений. Относительную частоту обычно обозначают буквой W. Если в n наблюдениях событие А наблюдается m раз, то относительная частота события А:
Например, баскетболист у штрафной линии готовится совершить бросок. Из собранной тренером статистической информации известно, что у этого баскетболиста из 100 штрафных бросков успешны 70. Вероятность того, что баскетболист реализует штрафной бросок:

Задачи:
1. Абонент забыл последние 2 цифры телефонного номера, но помнит, что они различны и образуют двузначное число, меньшее 30. С учетом этого он набирает наугад 2 цифры. Найти вероятность того, что это будут нужные цифры.
2. Шесть шаров случайным образом раскладывают в три ящика. Найти вероятность того, что во всех ящиках окажется разное число шаров, при условии, что все ящики не пустые.
3. Цифры 1, 2, 3, …, 9, выписанные на отдельные карточки складывают в ящик и тщательно перемешивают. Наугад вынимают одну карточку. Найти вероятность того, что число, написанное на этой карточке: а) четное; б) двузначное.
4. На полке в случайном порядке расставлено 40 книг, среди которых находится трехтомник Пушкина. Найти вероятность того, что эти тома стоят в порядке возрастания номера слева направо, но не обязательно рядом.
5. На каждой из пяти одинаковых карточек напечатана одна из следующих букв: "а", "м", "р", "т", "ю". Карточки тщательно перемешаны. Найти вероятность того, что на четырех вынутых по одной карточке можно прочесть слово "юрта".

6. В урне находится 15 белых, 5 красных и 10 чёрных шаров. Наугад извлекается 1 шар, найти вероятность того, что он будет: а) белым, б) красным, в) чёрным.
7. Найти вероятность выпадения числа 5 в результате бросания игральной кости.
8. В группе 30 студентов. Трём студентам следует направиться на кафедру информатики, чтобы взять и принести компьютер и проектор. Вычислить вероятность того, что это сделают три определённых студента.
9. Продаются 10 мобильных телефонов. Из них у 3 есть дефекты. Покупатель выбрал 2 телефона. Вычислить вероятность того, что оба выбранных телефона будут с дефектами.
10. В лифт 20-этажного дома на первом этаже зашли 3 человека. И поехали. Найти вероятность того, что:
а) они выйдут на разных этажах
б) двое выйдут на одном этаже;
в) все выйдут на одном этаже.
11. Какова вероятность того, что в четырех сданных картах будет один туз и один король?