Признак перпендикулярности прямой и плоскости

2-й урок по теме «Перпендикулярность
прямых и плоскостей».
Повторить:
-определение перпендикулярных прямых;
-лемма;
-определение прямой, перпендикулярной
к плоскости;
-теорема о параллельных прямых,
перпендикулярных к плоскости
(прямая и обратная)

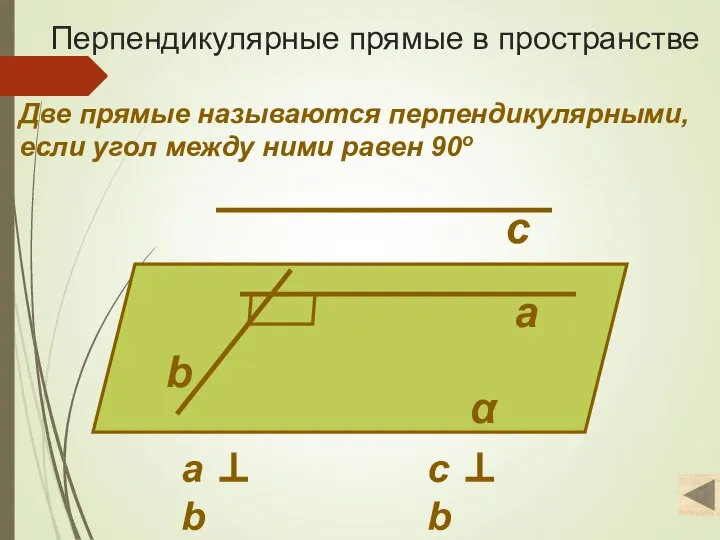
Перпендикулярные прямые в пространстве
Две прямые называются перпендикулярными,
если угол между ними равен 90о
а
b
с
а ⊥ b
c ⊥ b
α

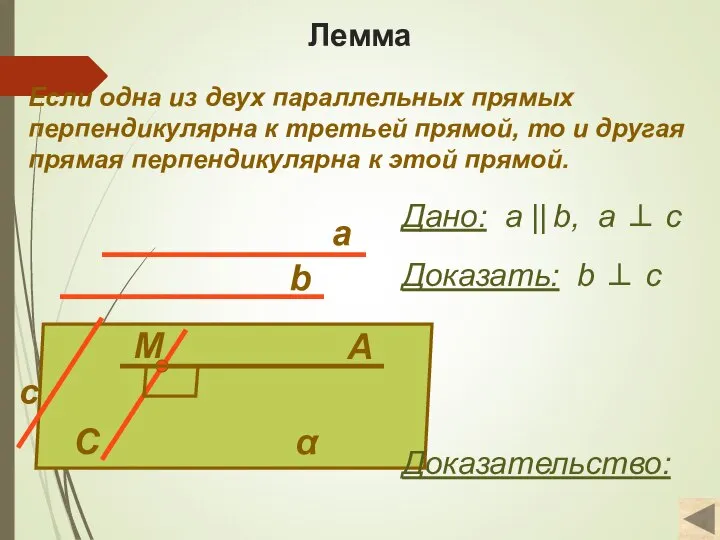
Лемма
Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
A
C
a
α
M
b
c
Дано: а || b, a ⊥ c
Доказать: b ⊥ c
Доказательство:

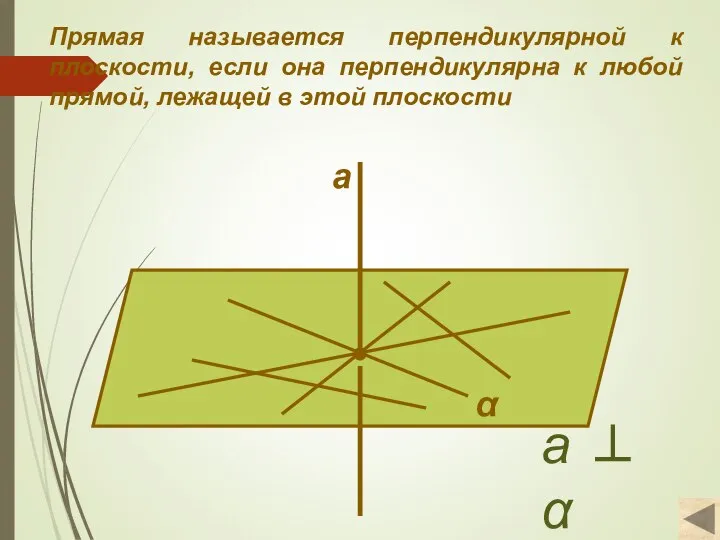
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости
α
а
а ⊥ α

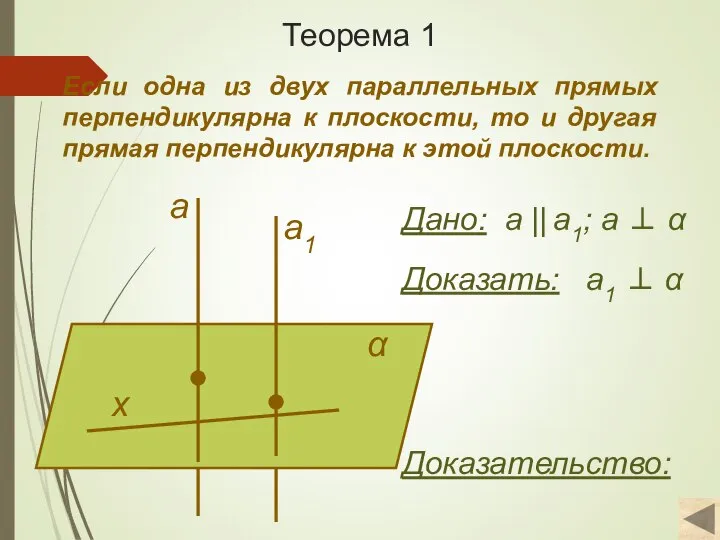
Теорема 1
Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
α
х
Дано: а || а1; a ⊥ α
Доказать: а1 ⊥ α
Доказательство:

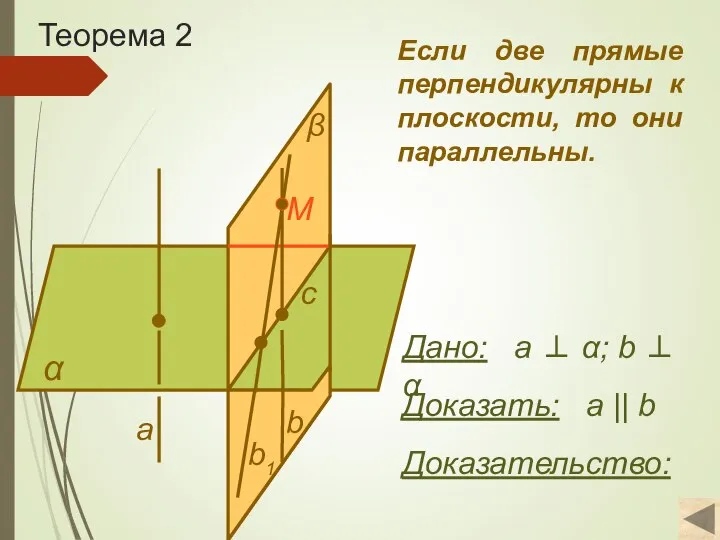
Теорема 2
α
Доказать: а || b
Доказательство:
Если две прямые перпендикулярны к плоскости, то они параллельны.
Дано: а ⊥ α; b ⊥ α
M
с

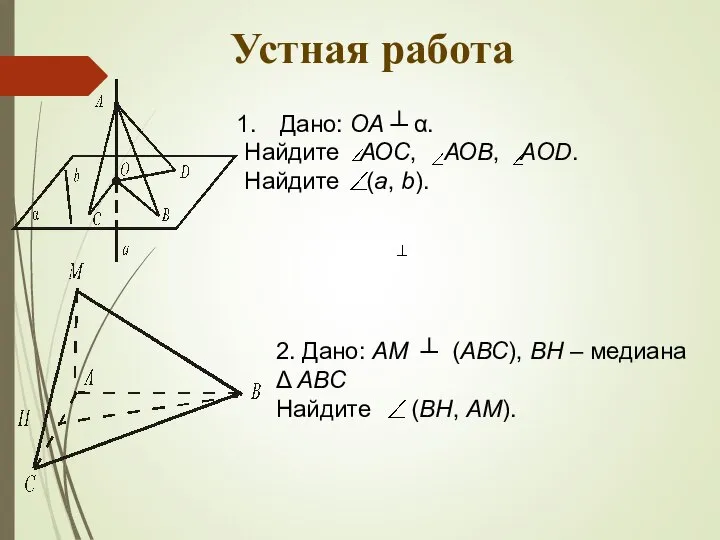
Устная работа
Дано: ОА ┴ α.
Найдите АОС, АОВ, AOD.
Найдите (а, b).
2. Дано: АМ ┴ (АВС), ВН – медиана Δ АВС
Найдите (ВН, АМ).

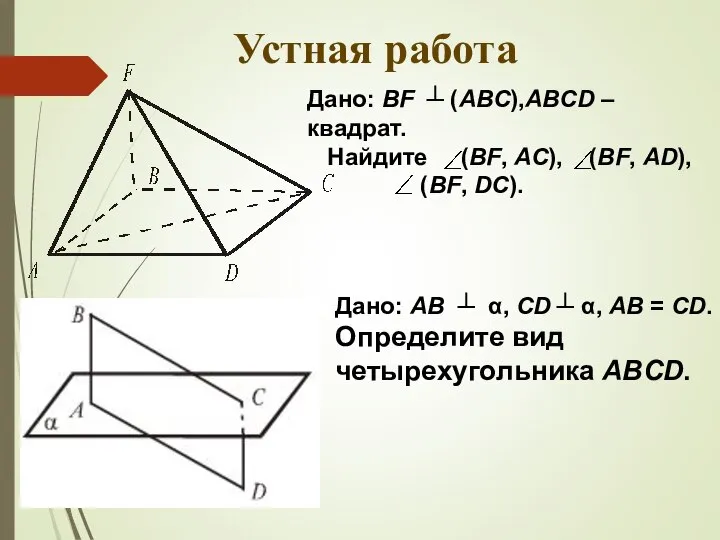
Устная работа
Дано: BF ┴ (АВС),ABCD – квадрат.
Найдите (BF, АС), (BF, AD),
(BF, DC).
Дано: АВ ┴ α, CD ┴ α, AB = CD.
Определите вид четырехугольника ABCD.

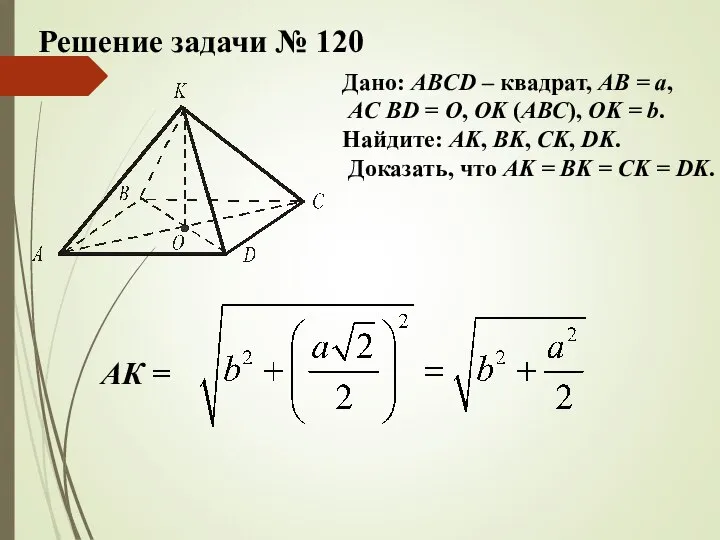
Решение задачи № 120
Дано: ABCD – квадрат, АВ = а,
АС BD = О, ОK (АВС), ОK = b.
Найдите: АK, ВK, СK, DK.
Доказать, что АK = ВK = СK = DK.
АК =

ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ
ПРЯМОЙ И ПЛОСКОСТИ
Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости

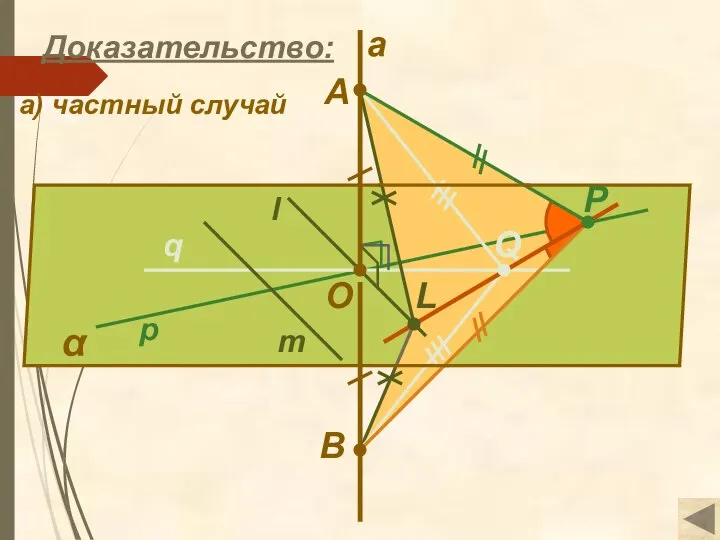
α
q
l
m
O
a
p
B
P
Q
Доказательство:
L
а) частный случай
A

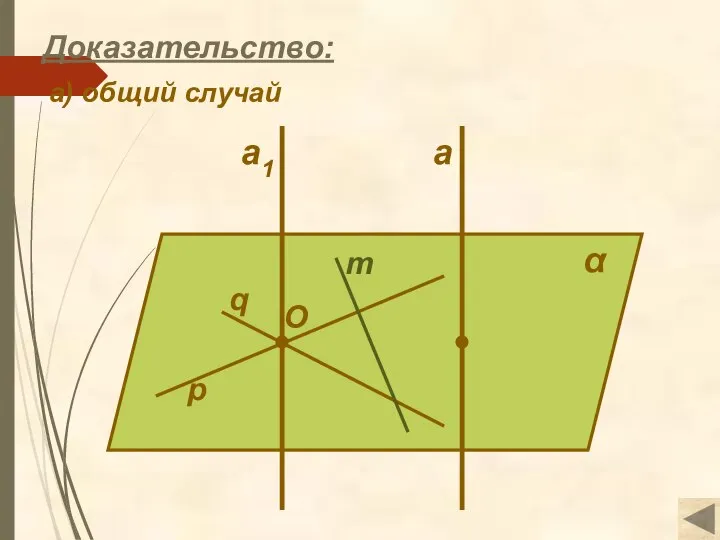
α
q
a
p
m
O
Доказательство:
а) общий случай
a1

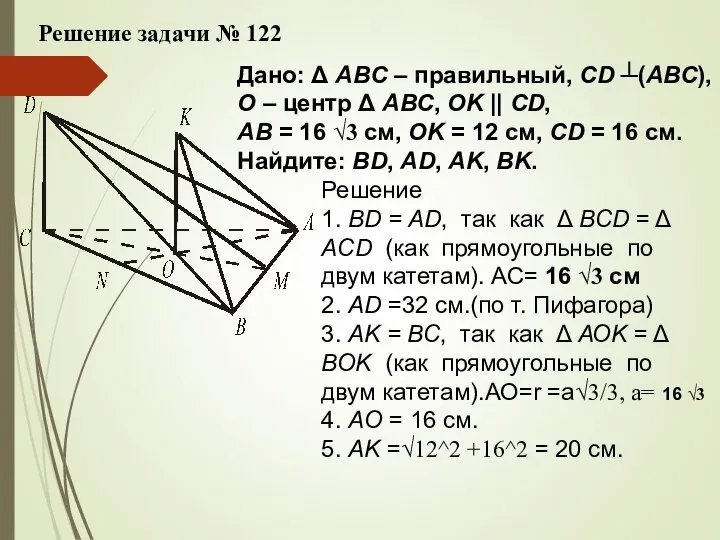
Решение задачи № 122
Дано: Δ ABC – правильный, CD ┴(АВС), О – центр Δ АВС, ОK || CD,
АВ = 16 √3 см, ОK = 12 см, CD = 16 см.
Найдите: BD, AD, АK, ВK.
Решение
1. BD = AD, так как Δ BCD = Δ ACD (как прямоугольные по двум катетам). АС= 16 √3 см
2. AD =32 см.(по т. Пифагора)
3. АK = ВС, так как Δ АОK = Δ ВОK (как прямоугольные по двум катетам).АО=r =a√3/3, а= 16 √3
4. AO = 16 см.
5. АK =√12^2 +16^2 = 20 см.

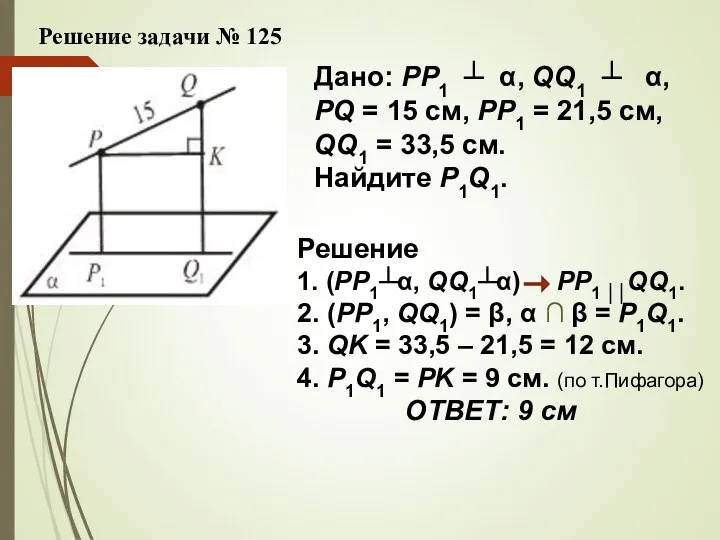
Решение задачи № 125
Дано: РР1 ┴ α, QQ1 ┴ α,
PQ = 15 см, РР1 = 21,5 см, QQ1 = 33,5 см.
Найдите P1Q1.
Решение
1. (РР1┴α, QQ1┴α) РР1 ││QQ1.
2. (РР1, QQ1) = β, α ∩ β = P1Q1.
3. QK = 33,5 – 21,5 = 12 см.
4. P1Q1 = РK = 9 см. (по т.Пифагора)
ОТВЕТ: 9 см

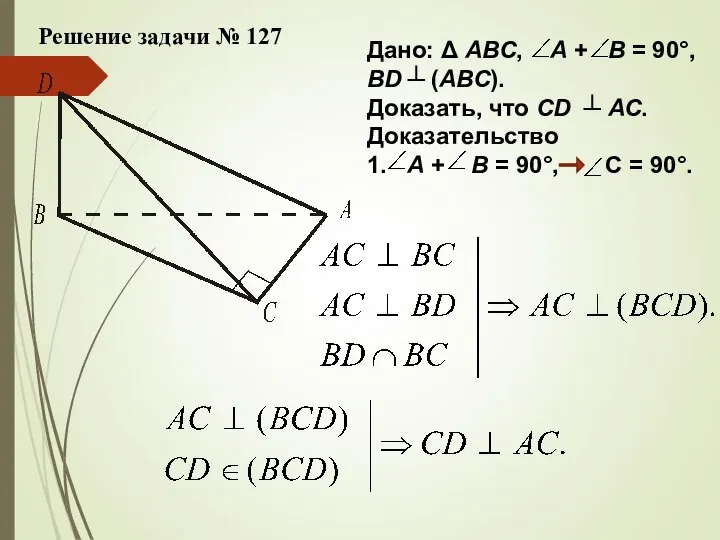
Решение задачи № 127
Дано: Δ АВС, А + В = 90°,
BD ┴ (АВС).
Доказать, что CD ┴ АС.
Доказательство
1. А + В = 90°, С = 90°.