Второй и третий признаки равенства треугольников. LOGO

План урока.
1
Математический диктант
2
Объяснение нового материала.
3
Решение задач.

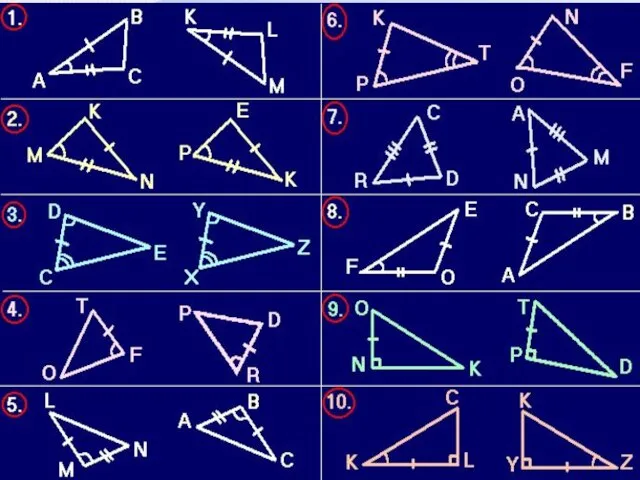
Тест «Свойства равнобедренного треугольника»

Тест «Свойства равнобедренного треугольника». Проверка.

Задача № 1.
Периметр равнобедренного треугольника равен 70 см. Найдите стороны этого треугольника, если его боковая сторона относится к основанию как 5:4.

Задача № 2.
Периметр равнобедренного треугольника равен 48 см. Найдите стороны этого треугольника, если его основание составляет 0,4 боковой стороны.

Задача № 3.
В треугольнике АВС проведена медиана ВЕ. Найдите длину АЕ, если АВ=6 см, периметр треугольника АВС равен 18 см, а ВС на 2 см больше АВ.
Задача № 4.
Периметр треугольника равен 40 см. Медиана делит данный треугольник на два треугольника, периметры которых равны 28 см и 24 см. Найдите длину медианы.

Второй признак равенства треугольников
Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
Дано:
ΔАВС; ΔА1В1С1; АВ=А1В1;
∠А =∠А1, ∠В=∠В1.
Доказать: ΔАВС=ΔА1В1С1

В
А
С
А1
В1
С1
Доказательство
Наложим треугольник ∆ABC на ∆А1В1С1, так чтобы вершина A совместилась с вершиной A1, вершины B и B1 лежали по одну сторону от A1C1.
Так как ∠А =∠А1, ∠В=∠В1, то AС наложится на луч A1С1, BC наложится на луч B1C1 (по аксиоме откладывания угла).
Вершина С – с вершиной С1 (по аксиоме откладывания отрезка).
Стороны треугольников BС и B1С1, АС и А1С1совместятся (по аксиоме откладывания отрезка).
Треугольник ABC и треугольник А1В1С1 полностью совместится →∆АВС = ∆А1В1С1

Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Дано:
ΔАВС; ΔА1В1С1; АВ=А1В1; АС=А1С1; ВС=В1С1.
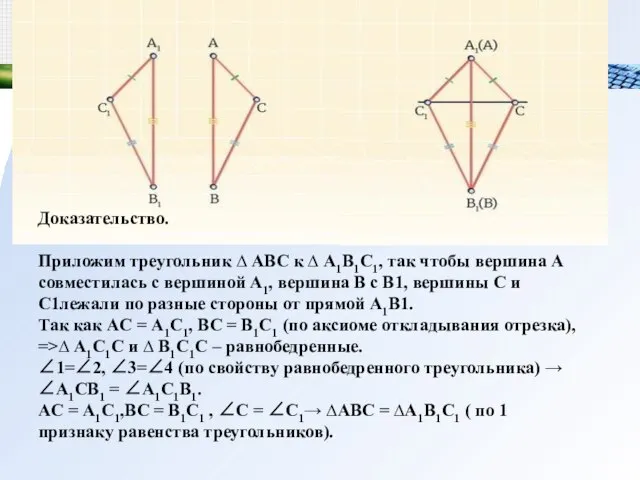
Доказать: ΔАВС=ΔА1В1С1

Доказательство.
Приложим треугольник ∆ ABC к ∆ А1В1С1, так чтобы вершина A совместилась с вершиной A1, вершина B с B1, вершины C и C1лежали по разные стороны от прямой A1B1.
Так как АC = А1C1, BC = B1C1 (по аксиоме откладывания отрезка), =>∆ А1C1С и ∆ В1С1C – равнобедренные.
∠1=∠2, ∠3=∠4 (по свойству равнобедренного треугольника) → ∠A1CB1 = ∠А1С1В1.
АC = А1C1,BC = B1C1 , ∠C = ∠C1→ ∆АВС = ∆А1В1С1 ( по 1 признаку равенства треугольников).

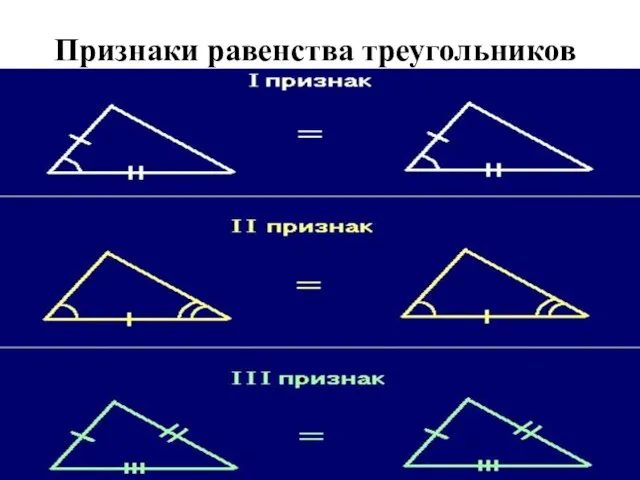
Признаки равенства треугольников