- Главная
- Математика
- Путешествие в историю математики. Решение старинных задач

Содержание
- 2. Старинная задача (Китай) Условие: в клетке находится неизвестное число фазанов и кроликов.Известно, что вся клетка содержит
- 3. Старинная задача (Франция, XVII – XVIII в. в.) Условие: трое хотят купить дом за 24000 ливров.
- 4. Старинная задача (Индия, III-IV века н.э.) Условие: из четырех жертвователей второй дал вдвое больше первого,третий —
- 5. Из «Всеобщей арифметики» И.Ньютона Условие:некто желает распределить между бедными деньги. Если бы у него было на
- 6. Из «Арифметики» Л.Н.Толстого Условие: у двух мужиков 35 овец. У одного на 9 овец больше, чем
- 7. Старинная задача из «Арифметики» Л.Ф.Магницкого Условие: лошадь съедает воз сена за месяц, коза — за два
- 8. Список используемой литературы 1. История развития математики. [Элекстронный ресурс]. URL: http://imcs.dvfu.ru/lib/eastprog/math_history.html 2. Архив рубрики «Старинные задачи
- 10. Скачать презентацию
Слайд 2Старинная задача (Китай)
Условие: в клетке находится неизвестное число фазанов и кроликов.Известно, что
Старинная задача (Китай)
Условие: в клетке находится неизвестное число фазанов и кроликов.Известно, что

Решение:Пусть в клетке одни кролики. Тогда число ног составит 35*4 = 140. Но на самом деле в клетке на 140 – 94 = 46 (ног) меньше, поскольку часть из них принадлежит фазанам, у которых на две ноги меньше, чем у кроликов. Значит число фазанов составляет 46:2 = 23, а число кроликов, соответственно, 35 – 23 = 12.
Слайд 3Старинная задача (Франция, XVII – XVIII в. в.)
Условие: трое хотят купить дом
Старинная задача (Франция, XVII – XVIII в. в.)
Условие: трое хотят купить дом

Решение: это очень простая задача на дроби. Первый даст половину всей суммы, то есть 24000:2 = 12000 (ливров). Второй – 1/3, то есть 24000:3 = 8000 (ливров), а третий – оставшуюся сумму, то есть 24000 – 12000 – 8000 = 4000 (ливров)
Слайд 4Старинная задача (Индия, III-IV века н.э.)
Условие: из четырех жертвователей второй дал вдвое
Старинная задача (Индия, III-IV века н.э.)
Условие: из четырех жертвователей второй дал вдвое

первого,третий — втрое больше второго, четвертый —
вчетверо больше третьего, все вместе дали 132 (денежных
единицы). Сколько дал первый?
Решение: пусть первый дал одну часть, тогда, согласно условию, второй дал 2 части, третий – 6 частей, четвёртый – 24 части. Всё пожертвование в размере 132 денежных единиц составило, таким образом, 1 + 2 + 6 +24 = 33 части и, следовательно, на одну часть приходится 4 денежных единицы. Первый жертвователь дал одну часть – 4 денежные единицы.
Слайд 5Из «Всеобщей арифметики» И.Ньютона
Условие:некто желает распределить между бедными деньги. Если бы у
Из «Всеобщей арифметики» И.Ньютона
Условие:некто желает распределить между бедными деньги. Если бы у

Решение: некто раздал бедным по два динара, а оставшиеся у него 3 начал добавлять каждому бедному с тем, чтобы к него стало 3 динара. Таких людей оказалось трое. Согласно условию, для того, чтобы у всех участников стало по 3 динара, не хватило 8 динаров. Значит всего бедных было 3 + 8 = 11.
«Всеобщая арифметика» И.Ньютона
Слайд 6Из «Арифметики» Л.Н.Толстого
Условие: у двух мужиков 35 овец. У одного на
Из «Арифметики» Л.Н.Толстого
Условие: у двух мужиков 35 овец. У одного на

Решение:
Если бы у двух мужиков овец было поровну и по стольку, сколько было у того, у кого овец меньше, то в сумме у них было бы 35 – 9 = 26 (овец), а у каждого по 13 овец. Но у одного на самом деле было на 9 овец больше, то есть 13 + 9 = 22 (овцы)
Слайд 7Старинная задача из «Арифметики» Л.Ф.Магницкого
Условие: лошадь съедает воз сена за месяц, коза
Старинная задача из «Арифметики» Л.Ф.Магницкого
Условие: лошадь съедает воз сена за месяц, коза

Решение: За месяц коза съест 1/2 воза сена, а овца – 1/3. Следовательно, все три животных за месяц съедят 1 + 1/2 + 1/3 = 1 и 5/6 = 11/6 воза. Один воз будет ими съеден в 11/6 раза быстрее, то есть за 1:11/6 = 6/11 месяца.
Эту задачу можно решить и без дробей. Для удобства выберем наименьшее общее кратное чисел 2 и 3, являющееся числом 6. За 6 месяцев лошадь съест 6 возов сена, коза – 3, а овца – 2. Вместе три животных за 6 месяцев съедят 6 + 3 + 2 = 11 возов сена, а за месяц – в 6 раз меньше, то есть 11/6 воза.
«Арифметика» Л.Ф.Магницкого
Слайд 8Список используемой литературы
1. История развития математики. [Элекстронный ресурс]. URL: http://imcs.dvfu.ru/lib/eastprog/math_history.html
2. Архив рубрики
Список используемой литературы
1. История развития математики. [Элекстронный ресурс]. URL: http://imcs.dvfu.ru/lib/eastprog/math_history.html
2. Архив рубрики
![Список используемой литературы 1. История развития математики. [Элекстронный ресурс]. URL: http://imcs.dvfu.ru/lib/eastprog/math_history.html 2.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1033387/slide-7.jpg)
3. ''Старинные задачи.'' Книга для учащихся. Иван Иванович Баврин, Евгений Александрович. „Фрибус“. М., Просвещение, 1994.
4. „Живая математика.“ Я.И.Перельман, „Триада-Литера“, Москва, 1994.
5. Математический портал- «Математика.ру» [Электронный ресурс]. URL: http://matematiku.ru/index.php?option=com_content&task=view&id=2015&Itemid=40
6. Развитие математики на Руси. [Электронный ресурс]. URL:http://matematika.gym075.edusite.ru/zadachki/denegnir-racheti-1.htmlИстория развития математики. [Элекстронный ресурс]. URL: http://imcs.dvfu.ru/lib/eastprog/math_history.html
2. Архив рубрики «Старинные задачи по математике» [Электронный ресурс]. URL: http://uchimsya-reshat-zadach.ru/category/starinnyie-zadachi-po-matematike?fdx_switcher=true
3. ''Старинные задачи.'' Книга для учащихся. Иван Иванович Баврин, Евгений Александрович. „Фрибус“. М., Просвещение, 1994.
4. „Живая математика.“ Я.И.Перельман, „Триада-Литера“, Москва, 1994.
5. Математический портал- «Математика.ру» [Электронный ресурс]. URL: http://matematiku.ru/index.php?option=com_content&task=view&id=2015&Itemid=40
6. Развитие математики на Руси. [Электронный ресурс]. URL:http://matematika.gym075.edusite.ru/zadachki/denegnir-racheti-1.html
 Признаки параллельности прямых
Признаки параллельности прямых Задача с экологическим содержанием
Задача с экологическим содержанием Разные задачи. Способ Пропорция
Разные задачи. Способ Пропорция Иррациональные уравнения. Открытый урок
Иррациональные уравнения. Открытый урок Необычные способы вычислений
Необычные способы вычислений Путешествие в зазеркалье. Проект по геометрии
Путешествие в зазеркалье. Проект по геометрии Уходя, гасите свет. Математические расчеты
Уходя, гасите свет. Математические расчеты Байесовский анализ и сети Байеса
Байесовский анализ и сети Байеса Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью
Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью Конструирование из счётных палочек
Конструирование из счётных палочек Содержание кривых участков пути. Переходные кривые
Содержание кривых участков пути. Переходные кривые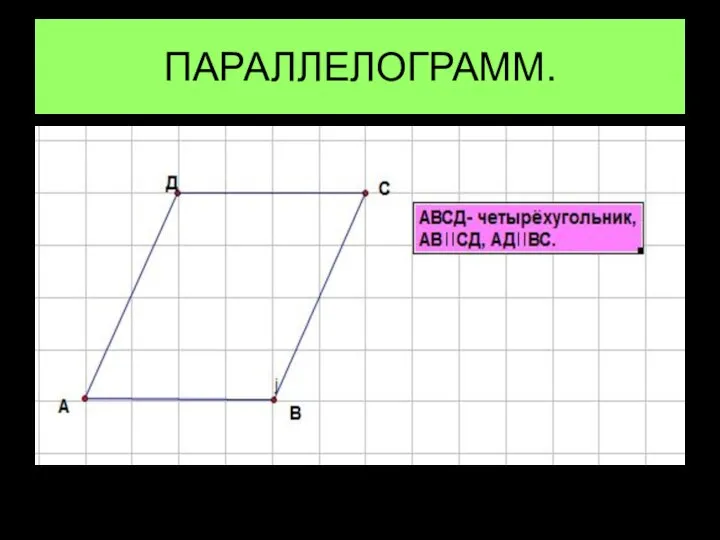 Параллелограмм. Свойства. Признаки
Параллелограмм. Свойства. Признаки В гостях у геометрических фигур
В гостях у геометрических фигур Сложение отрицательных чисел
Сложение отрицательных чисел Квадратичная функция. Наглядно-методическое пособие. 9 класс
Квадратичная функция. Наглядно-методическое пособие. 9 класс Решение задач по теме Правильные многоугольники
Решение задач по теме Правильные многоугольники Дидактические игры в детском саду
Дидактические игры в детском саду Решение задач на вычисление площади поверхности призмы
Решение задач на вычисление площади поверхности призмы Бином Ньютона. Треугольник Паскаля. Решение задач
Бином Ньютона. Треугольник Паскаля. Решение задач Задуманное число. Общий множитель
Задуманное число. Общий множитель Вероятность распределения случайных чисел
Вероятность распределения случайных чисел Конус. Цилиндр. Сфера
Конус. Цилиндр. Сфера Множество значений тригонометрических функций
Множество значений тригонометрических функций Квадратные неравенства
Квадратные неравенства Числа от 1 до 1000, умножение и деление. Приемы устных вычислений
Числа от 1 до 1000, умножение и деление. Приемы устных вычислений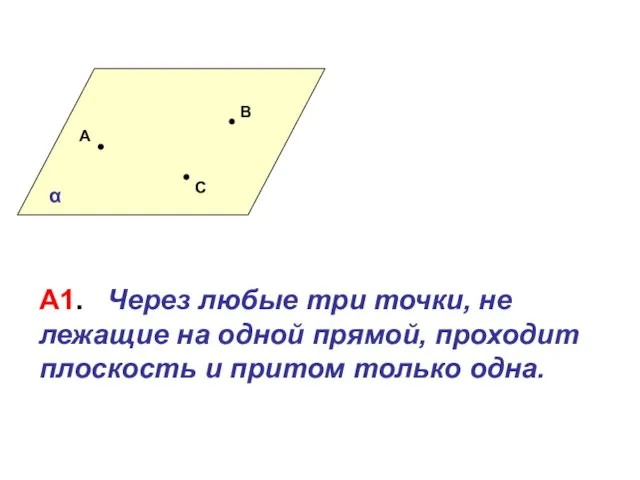 Плоскости
Плоскости Решение задач составлением систем уравнений с двумя переменными
Решение задач составлением систем уравнений с двумя переменными Линейные дифференциальные уравнения первого порядка
Линейные дифференциальные уравнения первого порядка