Содержание
- 2. Основные определения Уравнением называется два алгебраичес-ких выражения, соединенные знаком равенства (=). Корнем уравнения называется такое значение
- 3. Линейное уравнение с одним неизвестным (общий вид) ах + b = 0 а, b – любые
- 4. ах + b = 0 Ничего сложного, правда? Особенно, если не замечать слова: "где а и
- 5. Всё решение линейных уравнений состоит из тождественных преобразований уравнений. Кстати, эти преобразования (целых два!) лежат в
- 6. При решении уравнений используют теоремы о равносильности, которые мы рассмотрим на примере линейных уравнений. Равносильными называются
- 7. Теорема 1. Если к обеим частям уравнения прибавить одно и то же число, то полученное уравнение
- 8. Для решения линейных уравнений надо: Слагаемые, зависящие от х, перенести в одну часть уравнения, числа –
- 9. Для начала рассмотрим самый простой пример. х - 3 = 2 - 4х Это линейное уравнение.
- 10. Решим что-нибудь посолиднее. Что вам больше всего не нравится в этом уравнении? 95 человек из 100
- 11. Берём на заметку: чтобы привести исходное замороченное уравнение к приятному виду, мы использовали две (всего две!)
- 12. Особые случаи при решении линейных уравнений. Сюрприз первый. Предположим, попалось вам элементарнейшее уравнение: 2х+3=5х+5 - 3х
- 13. Сюрприз второй. Возьмём то же линейное уравнение и изменим в нём всего одно число. Вот такое
- 14. Ответы даны в беспорядке: 2,5; нет решений; 51; 17. Получилось?! Поздравляю! Теперь, когда мы разобрались со
- 16. Скачать презентацию













 Сечение куба и сечение тетраэдра
Сечение куба и сечение тетраэдра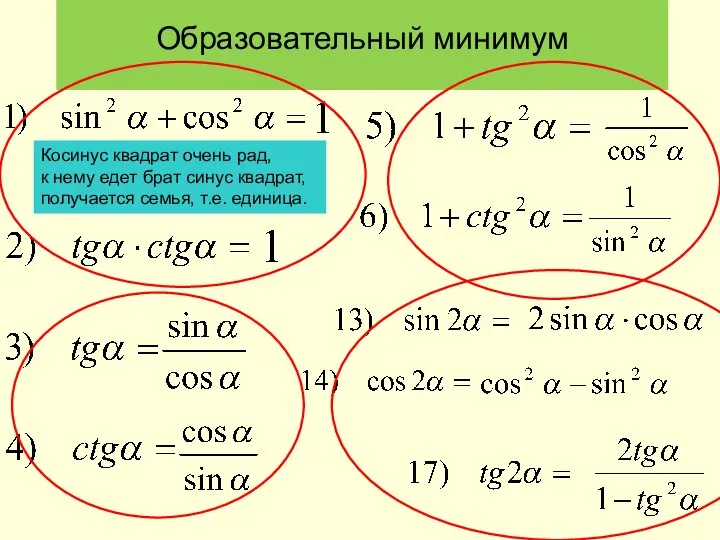 Образовательный минимум
Образовательный минимум Разложение многочлена на множители. Работа над ошибками
Разложение многочлена на множители. Работа над ошибками Путешествуем по странам Европы. 3 класс
Путешествуем по странам Европы. 3 класс Формулы нахождения объёма параллелеппипеда, объёма куба
Формулы нахождения объёма параллелеппипеда, объёма куба Теория вероятности. События и испытания
Теория вероятности. События и испытания Случаи вычитания 11-
Случаи вычитания 11- Оценка математического ожидания и дисперсии отклика в отдельных точках факторного пространства
Оценка математического ожидания и дисперсии отклика в отдельных точках факторного пространства Презентация на тему Является ли система координат чисто математическим понятием
Презентация на тему Является ли система координат чисто математическим понятием  Презентация на тему Владимир Модестович Брадис
Презентация на тему Владимир Модестович Брадис  Окружность. Основные теоремы
Окружность. Основные теоремы Мультипликативная система индексов
Мультипликативная система индексов Решение текстовых задач арифметическим способом
Решение текстовых задач арифметическим способом Случаи вычитания 12-
Случаи вычитания 12- Площа прямокутника
Площа прямокутника Первообразная
Первообразная Сравнение обыкновенной дроби и десятичной
Сравнение обыкновенной дроби и десятичной Линейные измерения
Линейные измерения Сложение и вычитание рациональных чисел
Сложение и вычитание рациональных чисел Деление одночлена на одночлен
Деление одночлена на одночлен Решение уравнений с помощью систем
Решение уравнений с помощью систем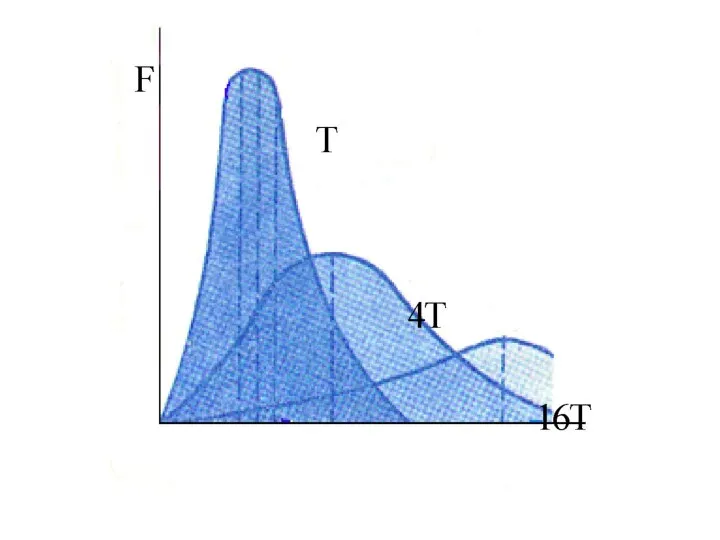 Функция распределения Максвелла
Функция распределения Максвелла Диаграммы. Виды диаграмм
Диаграммы. Виды диаграмм Одночлен и его стандартный вид
Одночлен и его стандартный вид Презентация на тему Площадь круга
Презентация на тему Площадь круга  Пять великих математиков
Пять великих математиков Медианы, биссектрисы и высоты треугольника. 7 класс
Медианы, биссектрисы и высоты треугольника. 7 класс Решение задач на параллельность прямых и плоскостей
Решение задач на параллельность прямых и плоскостей