Разложение вектора по базису

ТЕОРЕМА
Линейно независимая система векторов
в пространстве Rn является базисом
тогда и только тогда, когда число
векторов этой системы равно
размерности пространства n.

ТЕОРЕМА
Разложение любого вектора в данном
базисе является единственным.

Пусть система векторов
ДОКАЗАТЕЛЬСТВО:
является базисом.
Предположим, что вектор b может быть представлен в виде линейной комбинации базисных векторов двумя способами:

Причем наборы чисел
Получили, что линейная комбинация векторов системы равна нулю, т.е. Система оказалась линейно зависимой, что противоречит условию теоремы.
и
не совпадают.
Вычтем одно равенство из другого:
Следовательно, разложение вектора в данном базисе будет единственным.

Таким образом, в произвольном базисе пространства Rn любой вектор из этого пространства представим в виде разложения по базисным векторам:
Причем, это разложение является единственным для данного базиса.
Числа
называются координатами вектора
в базисе

Чтобы найти коэффициенты разложения αi в случае произвольного базиса, нужно приравнять соответствующие координаты линейной комбинации и координаты вектора
Пусть базисные вектора заданы в координатной форме:
И задан вектор

Тогда получим систему линейных уравнений:
Решая эту систему, находим коэффициенты разложения

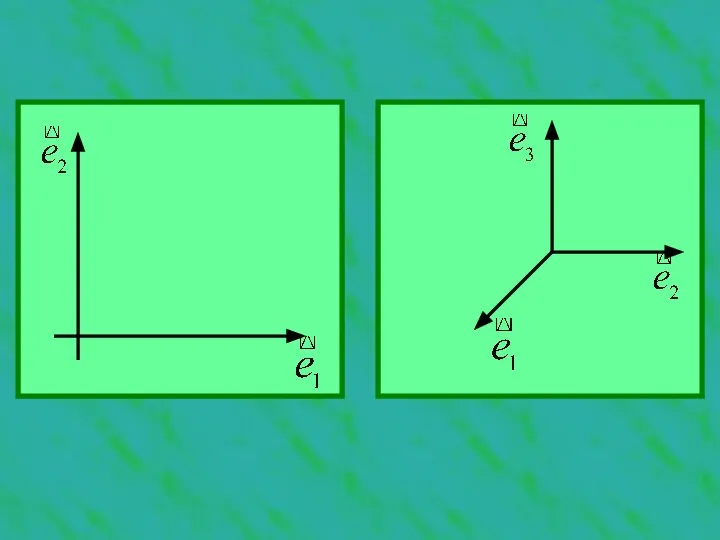
Рассмотрим базис пространства Rn , в котором каждый вектор ортогонален остальным векторам базиса:
Такой базис называется ортогональным.
Они хорошо представимы на плоскости и в пространстве:

Найдем разложение вектора
в ортогональном базисе:
Умножим обе части равенства на
Поскольку все вектора базиса взаимно ортогональны, то

Имеем:
В общем случае: