Содержание
- 2. Основные вопросы лекции #4 Постановка задачи синтеза регуляторов MIMO-систем. Основные этапы решения задачи синтеза систем управления.
- 3. Рассмотрим непараметрические (сигнальные) и параметрические возмущения. Структура обобщенного уравнения линейной системы и обобщенного входа позволяют введение
- 4. Определение 3.7. Матрица-столбец, составленная из субвекторов называется «обобщенным входом системы с непараметрическими возмущениями». Таким образом, обобщенное
- 5. К параметрическим возмущениям принято относить какие-либо изменения числовых или полиномиальных матриц коэффициентов, фигурирующих в формулах. Рассмотрим
- 6. Особенностью представленных параметрических возмущений является неразрушение общих свойств проматриц, рассмотренные ранее. Определение 3.8. Блочно-матричное уравнение связывающее
- 7. Реверсивная проблемная матрица системы Обобщенное уравнение линейной системы Обратное отображение
- 8. Репроматрица (обобщенная передаточная матрица) содержит все возможные передаточные матрицы от всех субвекторов, включенных в обобщенный вход,
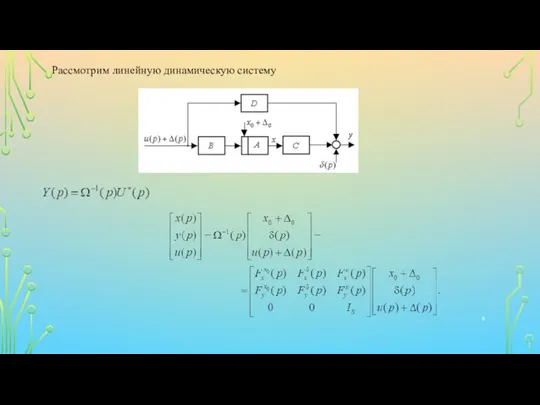
- 9. Рассмотрим линейную динамическую систему
- 10. Когда модели всех подсистем заданы уравнениями в пространстве состояния, то проматрица системы будет недробной. В этом
- 11. Другой метод обращения матриц (формула Фробениуса) основан на разбиении матрицы на блоки с последующим вычислением блоков
- 12. Рассмотрим проматрицу задачи моделирования Получение репроматрицы задачи моделирования можно осуществить, двукратно применяя формулу Фробениуса Пусть проматрица
- 13. Методика построения проматриц 1. Все подсистемы задаются обыкновенными линейными дифференциальными уравнениями с постоянными коэффициентами и линейными
- 14. 5. Из изображений начальных условий динамических объектов , а также входных сигналов статических и динамических устройств
- 15. – по возможности число статических подсистем за счет подстановок должно быть минимизировано; – каждую статическую подсистему,
- 17. Скачать презентацию













 Параллельные прямые
Параллельные прямые Угол между векторами
Угол между векторами Поле чудес. Геометрия
Поле чудес. Геометрия Единица массы - килограмм
Единица массы - килограмм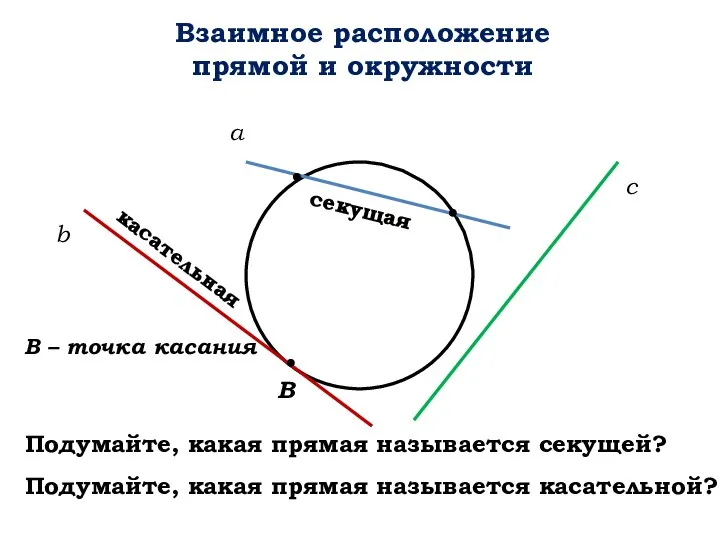 Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Действия с десятичными дробями 5 класс
Действия с десятичными дробями 5 класс Старинные системы мер
Старинные системы мер Лекция 8
Лекция 8 Линейная алгебра. Определители
Линейная алгебра. Определители Исследование функций и построение графиков
Исследование функций и построение графиков Координаты суммы, разности и произведения вектора на число
Координаты суммы, разности и произведения вектора на число 08.09
08.09 Графовые модели. Основные понятия. Принцип планирования многошаговых процессов
Графовые модели. Основные понятия. Принцип планирования многошаговых процессов Обработка результатов измерений при прямых однократных измерениях. Математические методы планирования активного эксперимента
Обработка результатов измерений при прямых однократных измерениях. Математические методы планирования активного эксперимента Веб – квест для учащихся 11 класса. Задачи по теме Производная
Веб – квест для учащихся 11 класса. Задачи по теме Производная Осевая симметрия
Осевая симметрия Задачи
Задачи Aproximarea numerică a funcţiilor. Metode numerice – curs 10
Aproximarea numerică a funcţiilor. Metode numerice – curs 10 Случайные величины. Таблицы распределения
Случайные величины. Таблицы распределения Условия неопределенности выбора. Ограниченная рациональность
Условия неопределенности выбора. Ограниченная рациональность Арифметический квадратный корень
Арифметический квадратный корень Степень многочлена
Степень многочлена Презентация на тему Методы решения квадратных уравнений
Презентация на тему Методы решения квадратных уравнений  Презентация на тему Противоположные числа (6 класс)
Презентация на тему Противоположные числа (6 класс)  Начертательная геометрия
Начертательная геометрия Тригонометрические функции острого угла прямоугольного треугольника. Решение прямоугольных треугольников
Тригонометрические функции острого угла прямоугольного треугольника. Решение прямоугольных треугольников Определение координаты движущегося тела
Определение координаты движущегося тела Умножение и деление комплексных чисел
Умножение и деление комплексных чисел