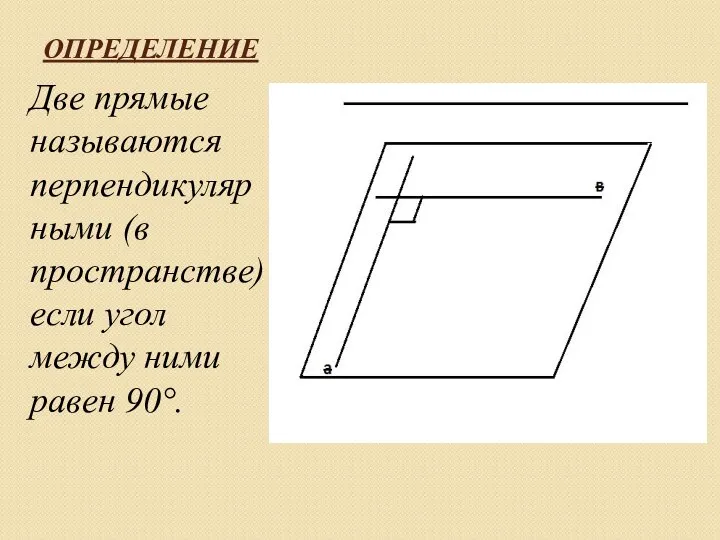
Слайд 2ОПРЕДЕЛЕНИЕ
Две прямые называются перпендикулярными (в пространстве) если угол между ними равен 90°.
Слайд 3ЛЕММА
Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и
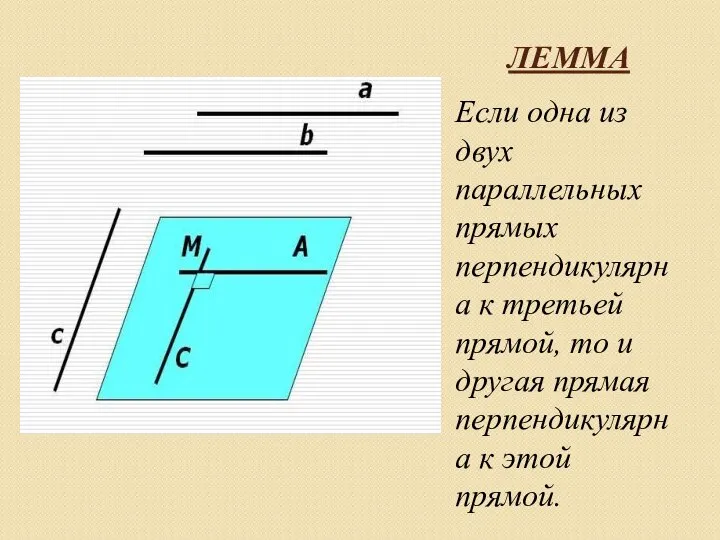
другая прямая перпендикулярна к этой прямой.
Слайд 4ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ, ПЕРПЕНДИКУЛЯРНЫЕ К ПЛОСКОСТИ

Слайд 5ОПРЕДЕЛЕНИЕ
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей
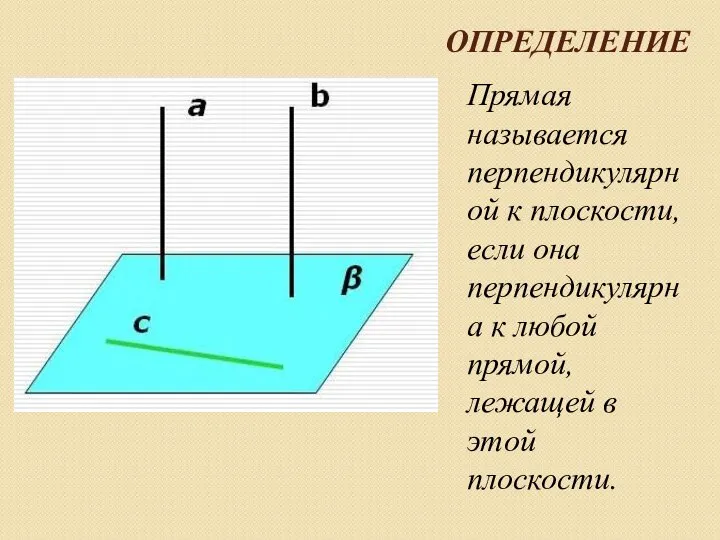
в этой плоскости.
Слайд 6ТЕОРЕМА
Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая
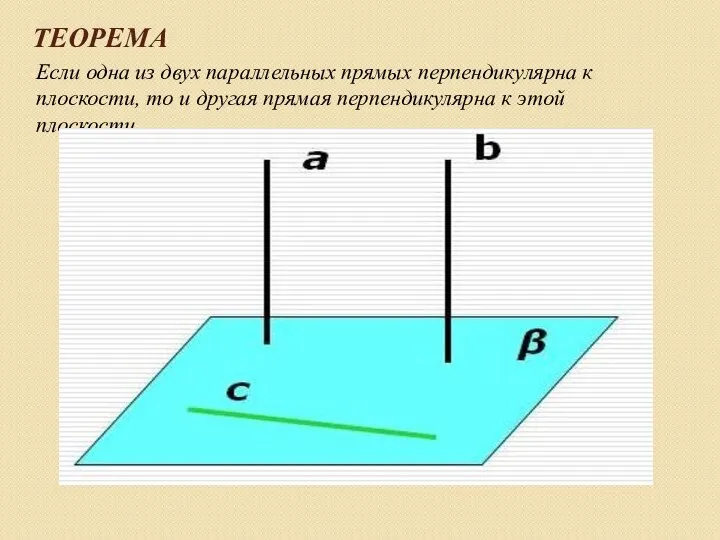
прямая перпендикулярна к этой плоскости.
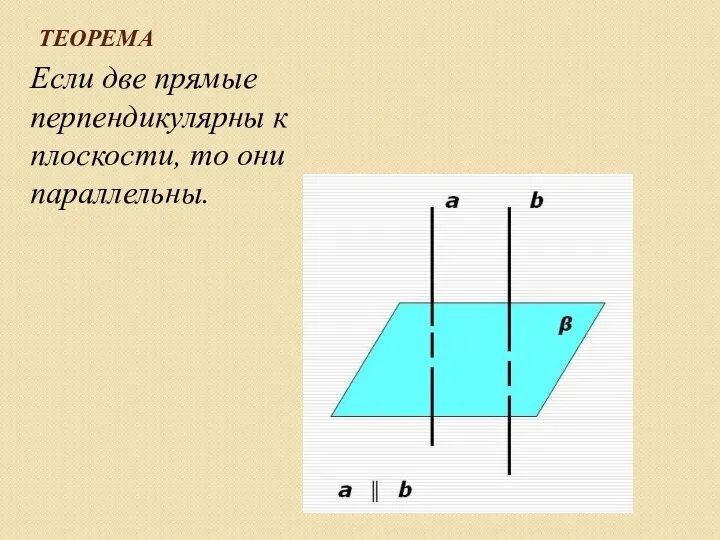
Слайд 7ТЕОРЕМА
Если две прямые перпендикулярны к плоскости, то они параллельны.
Слайд 817. ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ

Слайд 9ТЕОРЕМА
Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она
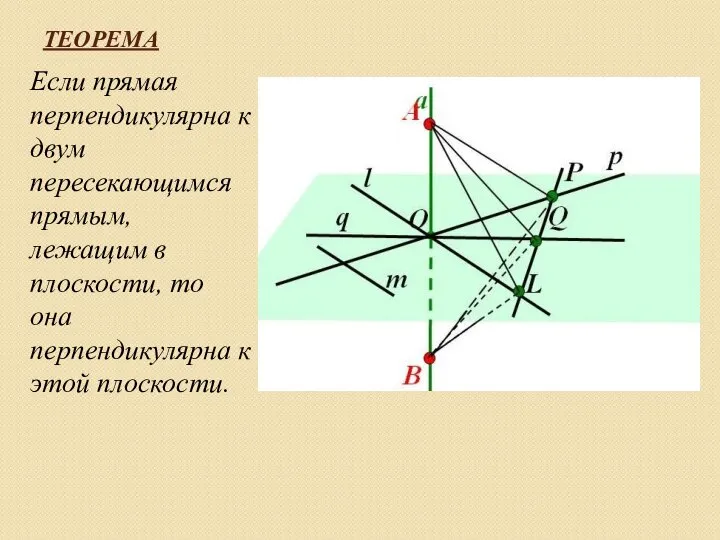
перпендикулярна к этой плоскости.
Слайд 1018.ТЕОРЕМА О ПРЯМОЙ, ПЕРПЕНДИКУЛЯРНОЙ К ПЛОСКОСТИ

Слайд 11Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом
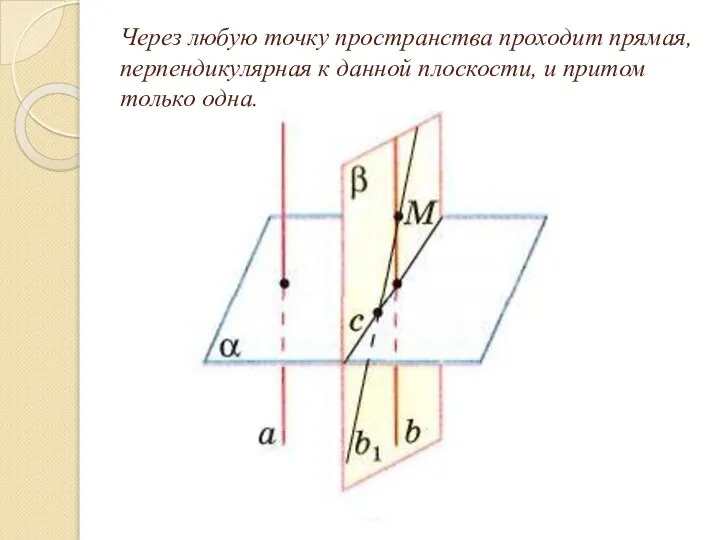
только одна.










 Презентация на тему Счёт предметов (1 класс)
Презентация на тему Счёт предметов (1 класс)  Факториал
Факториал Действия со степенями. Корень n-ой степени. Степень с рациональным показателем
Действия со степенями. Корень n-ой степени. Степень с рациональным показателем Скалярное произведение векторов
Скалярное произведение векторов Таблица умножения трёх
Таблица умножения трёх Визуальный и измерительный контроль
Визуальный и измерительный контроль Погрешность средства измерений
Погрешность средства измерений Своя игра по математике
Своя игра по математике Анализ геометрических высказываний
Анализ геометрических высказываний Показательные уравнения, сводящиеся к квадратным
Показательные уравнения, сводящиеся к квадратным Треугольник. Изображение. Обозначение
Треугольник. Изображение. Обозначение Сравниваем выражения. 2 класс
Сравниваем выражения. 2 класс Вычисление интегралов средствами MathCad
Вычисление интегралов средствами MathCad Логарифмически-нормальное (логонормальное) распределение
Логарифмически-нормальное (логонормальное) распределение Игра-тренажер Уроки с Мальвиной. Табличное умножение и деление
Игра-тренажер Уроки с Мальвиной. Табличное умножение и деление Выполни задания в электронном дневнике
Выполни задания в электронном дневнике Просто, сложно, интересно. Учебный курс предпрофильной подготовки для учащихся 9-х классов
Просто, сложно, интересно. Учебный курс предпрофильной подготовки для учащихся 9-х классов Стереометрия. Метод координат в задачах ЕГЭ
Стереометрия. Метод координат в задачах ЕГЭ Конкурс капитанов
Конкурс капитанов Презентация на тему Округление десятичных чисел
Презентация на тему Округление десятичных чисел  Презентация на тему Показательная функция
Презентация на тему Показательная функция  Разнообразный мир линий
Разнообразный мир линий Деление дробей
Деление дробей Консультация ДУ
Консультация ДУ Выполнение плана чертежа в масштабе
Выполнение плана чертежа в масштабе ЕГЭ Профиль - Задание 6
ЕГЭ Профиль - Задание 6 тригонометрия 1 урок
тригонометрия 1 урок Основы теории вероятностей. Лекция 113
Основы теории вероятностей. Лекция 113