Лекция №5. Основные понятия теории вероятностей и математической статистики

План
События.
Комбинации событий. Противоположные события.
Вероятность события.
Сложение вероятностей.
Независимые события. Умножение вероятностей.
Статистическая вероятность.
Элементы математической статистики

1. События.

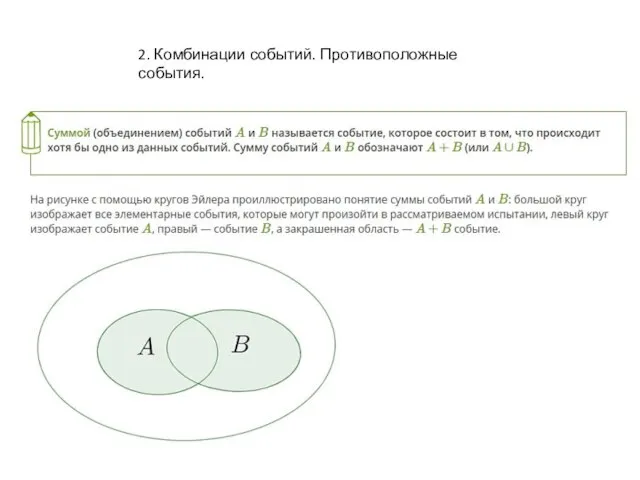
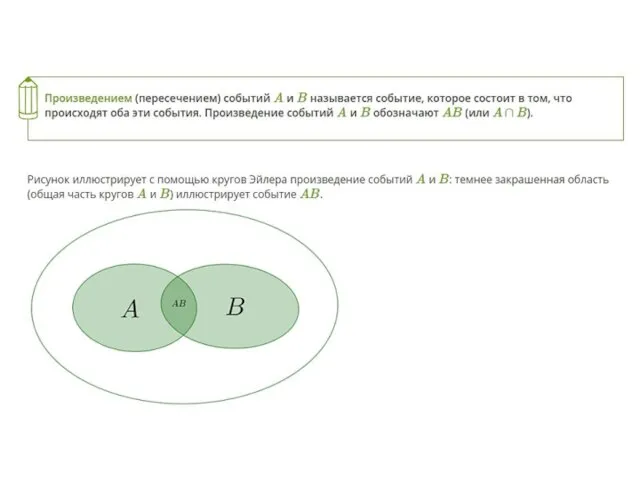
2. Комбинации событий. Противоположные события.

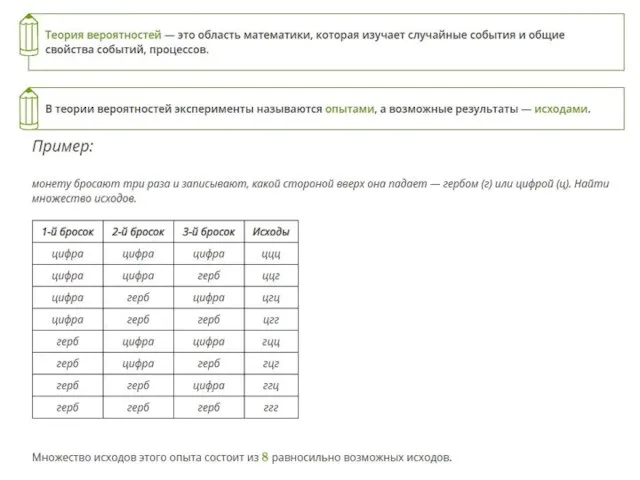
3. Вероятность события.

4. Сложение вероятностей.

5. Независимые события. Умножение вероятностей.

6. Статистическая вероятность.

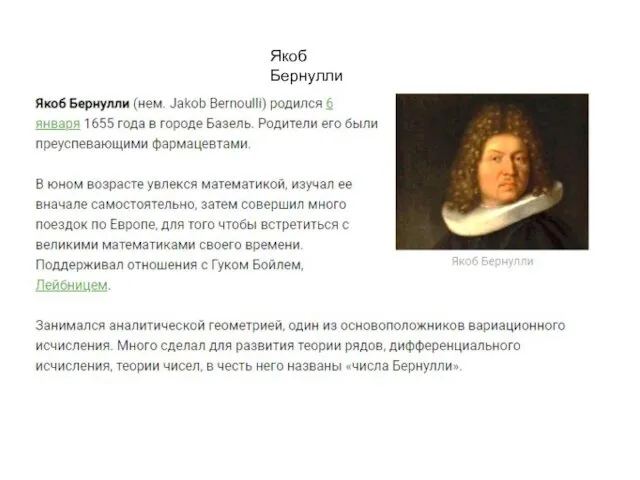
Якоб Бернулли

Давайте вспомним известные вам примеры, в которых информируется об итогах обработанной информации. (Средний прожиточный минимум на данный период, средняя продолжительность жизни, средняя зарплата по области, по стране; средняя успеваемость по группе, по колледжу; среднемесячная температура воздуха и т.д.)
Экономическая статистика изучает производство и потребление разнообразных видов продукции, изменение цен, спроса и предложения на товары, прогнозирует рост и падение производства и потребления, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и многое другое
Медицинская статистика изучает эффективность различных лекарств и методов лечения, вероятность возникновения некоторого заболевания в зависимости от возраста, пола, наследственности, условий жизни, вредных привычек, прогнозирует распространение эпидемий.
Демографическая статистика изучает рождаемость, численность населения, его состав (возрастной, национальный, профессиональный).
Есть еще статистика финансовая, налоговая, биологическая и т.д.

1.Статистика – это научное направление (комплекс наук), объединяющее принципы и методы работы с числовыми данными, характеризующими массовые явления.
2. Статистика – это отрасль практической деятельности, направленной на сбор, обработку, анализ статистических данных.
3. Статистика – это совокупность статистических данных, характеризующих какое-нибудь явление или процесс (например, статистика рождаемости и смертности в России, статистика успеваемости учащихся и т.п.).
Математическая статистика – это раздел математики который занимается разработкой методов сбора, описания и анализа экспериментальных результатов наблюдений, массовых случайных явлений..
Математическая статистика – наука, основанная на законах теории вероятностей. Статистические методы обработки данных из самых разных областей жизни имеют много общего. Это позволило создать универсальные научно обоснованные методы статистических исследований и проверки статистических гипотез.

Статистические характеристики – это математические понятия, с помощью которых описываются отличительные особенности и свойства совокупности данных, полученных с помощью наблюдений или каким-то другим способом.
Значение характеристик состоит еще и в том, что они «подсказывают», с каких позиций целесообразно анализировать имеющуюся совокупность данных.
Сбор информации: происходит массово или выборочно. При этом используется: перепись населения, отчеты предприятий, текущий учет, опросы, анкетирование, интервьюирование, наблюдения, статистика больниц, загсов и т.д.
Фундаментальными понятиями математической статистики являются генеральная совокупность и выборка. Генеральную совокупность удобно изображать с использованием круговой диаграммы, выборку – с использованием части круговой диаграммы.
Способы образования выборочной совокупности: случайная (отбирая на удачу), механическая (отбирая через определенный интервал), типическая (случайные выборки из каждой группы), серийная (разбивается на непересекающиеся серии или группы).

Обработка собранной информации.
Статистическая информация о результатах наблюдений или экспериментов может быть представлена в различных формах.
Простейшей из них является запись в порядке их появления – запись в ряд, называемый простым статистическим рядом или выборкой.
Отдельные значения, составляющие этот ряд, называют вариантами или просто данными.
Понятие объема ряда
Количество вариант в ряду n называют объемом ряда, или объемом выборки.
Варианты в ряду могут иметь как различные, так и одинаковые значения.
Понятие ранжированного ряда
Составить ранжированный ряд - это значит записать варианты в порядке их возрастания.

Характеристики числового ряда
Средним арифметическим (или выборочным средним) ряда чисел называется частное от деления суммы этих чисел на их количество.
Модой (Мо) называют число ряда, которое встречается в этом ряду наиболее часто.
Медианой ряда, состоящего из нечетного количества чисел, называется число данного ряда, которое окажется посередине, если этот ряд упорядочить.
Медианой ряда, состоящего из четного количества чисел, называется среднее арифметическое двух стоящих посередине чисел этого ряда, если этот ряд упорядочить.
Для того чтобы найти медиану ряда чисел, нужно сначала их упорядочить — составит ранжированный ряд (записать в порядке убывания).
Достоинством медианы является ее большая по сравнению со средним арифметическим «устойчивость к ошибкам».
Медиану используют вместо средней арифметической, когда крайние варианты упорядоченного ряда (наименьшая и наибольшая) по сравнению с остальными оказываются чрезмерно большими или чрезмерно малыми.

Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений.
Обработанные результаты статистики можно демонстрировать графически.
Пример: В первом полугодии 2011 года завод получил прибыль в 10 млн. рублей. Распределение прибыли по месяцам показано в таблице
В координатной плоскости на оси абсцисс будем отмечать номер месяца (янв. – 1, февр. – 2 и т.д.). На оси ординат будем отмечать прибыль завода (в млн. руб.). Отметим точки: (1;1,4),(2;1,3),(3;1,5),(4;2,1),(5;2),(6;1,7) и соединим их последовательно отрезками.

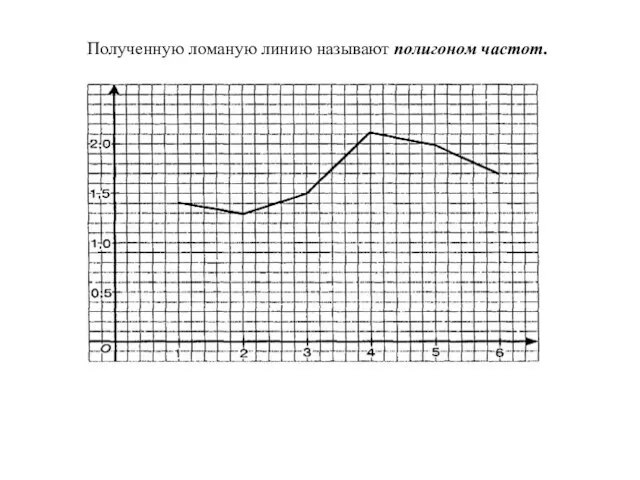
Полученную ломаную линию называют полигоном частот.

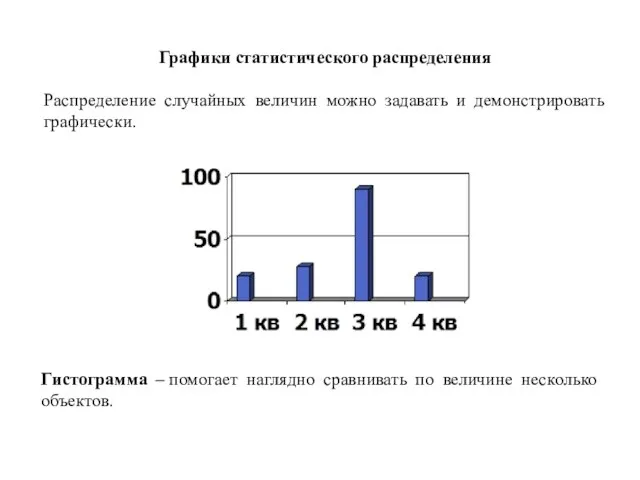
Графики статистического распределения
Распределение случайных величин можно задавать и демонстрировать графически.
Гистограмма – помогает наглядно сравнивать по величине несколько объектов.

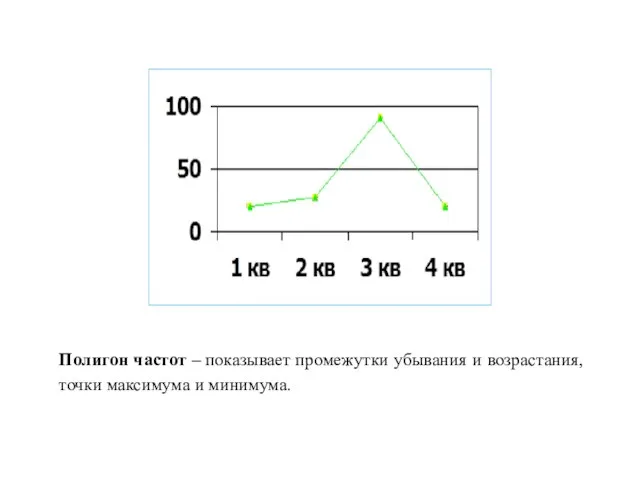
Полигон частот – показывает промежутки убывания и возрастания, точки максимума и минимума.

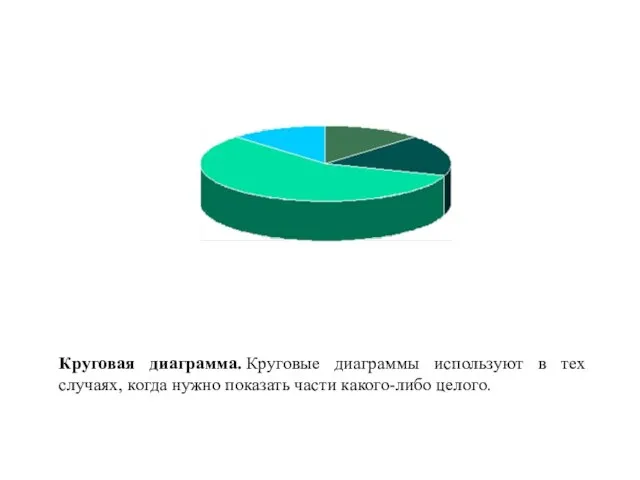
Круговая диаграмма. Круговые диаграммы используют в тех случаях, когда нужно показать части какого-либо целого.

Существуют и другие статистические характеристики, которые называются характеристиками отклонения.
Средние характеристики числового ряда позволяют оценить его поведение «в среднем». Но это далеко не всегда полностью характеризует выборку.
Размах — это разность наибольшего и наименьшего значений ряда данных.
Чтобы получить представление о поведении числового ряда, помимо средних характеристик надо знать характеристики разброса, показывающие, насколько значения ряда различаются между собой, как сильно они «разбросаны» вокруг средних. Простейшей такой характеристикой является размах.

В реальных статистических исследованиях чаще используют другую характеристику разброса, которая сложнее вычисляется, но зато меньше подвержена колебаниям.
Так появилось понятие дисперсии числового ряда.
Дисперсией числового ряда называется среднее арифметическое квадратов отклонений от среднего арифметического.
У дисперсии есть один существенный недостаток: если исходные значения ряда измеряются в каких-то единицах (например, в рублях), то у дисперсии эти единицы возводятся в квадрат («квадратные» рубли).
Избавиться от таких странных единиц измерения можно, если использовать другую характеристику разброса — стандартное отклонение.
Стандартным (или средним квадратичным) отклонением числового ряда называется квадратный корень из дисперсии.