Разложение вектора по двум неколлинеарным векторам. Координаты вектора

Разложение вектора по двум неколлинеарным векторам

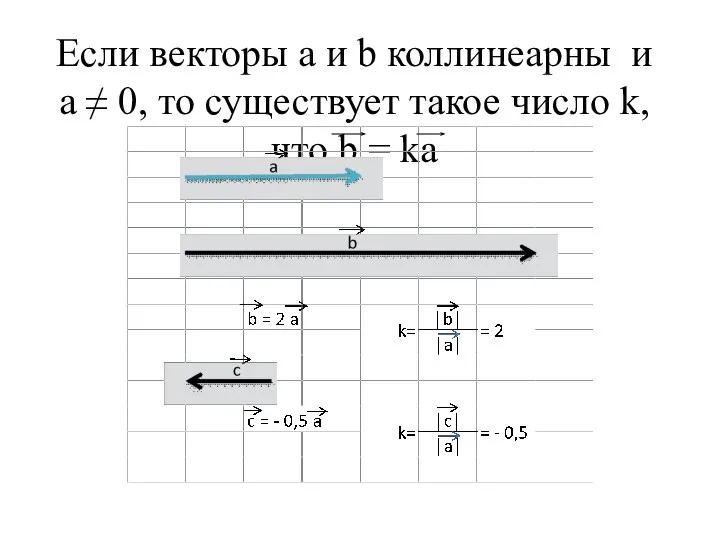
Если векторы а и b коллинеарны и а ≠ 0, то существует такое число k, что b = ka

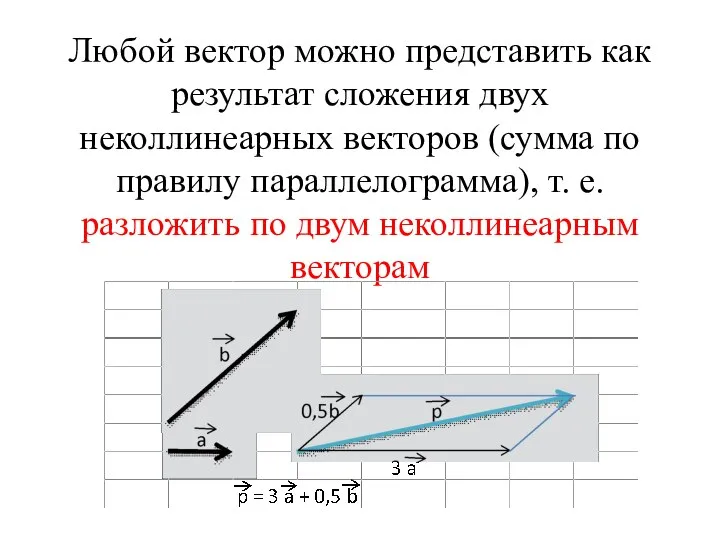
Любой вектор можно представить как результат сложения двух неколлинеарных векторов (сумма по правилу параллелограмма), т. е. разложить по двум неколлинеарным векторам

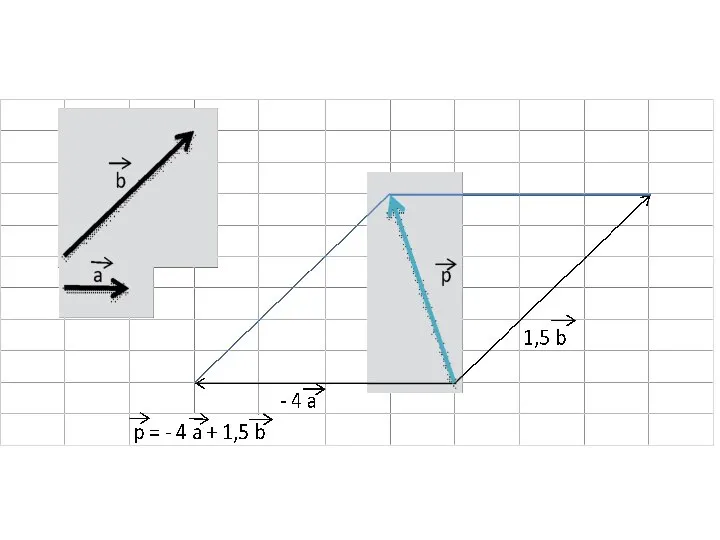
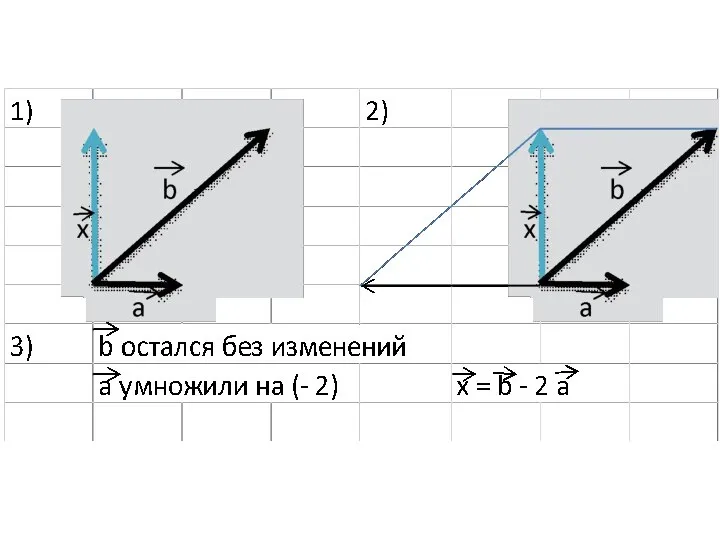
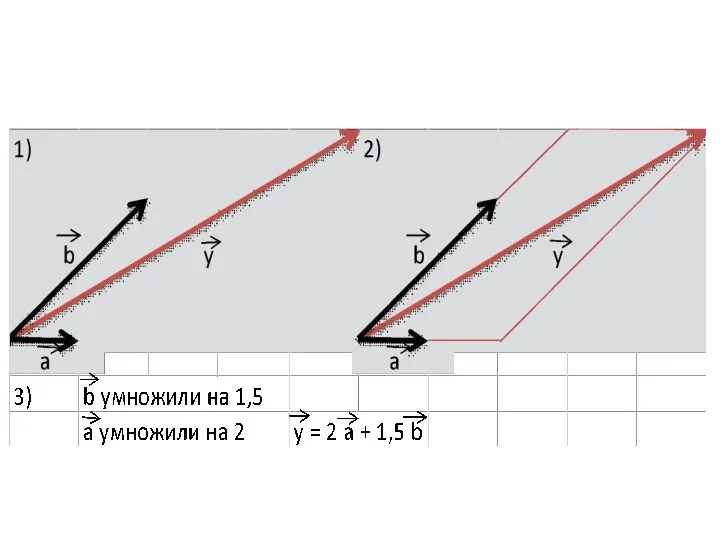
Чтобы разложить вектор по двум векторам надо:
1) отложить все три вектора от одной точки;
2) достроить до параллелограмма;
3) вычислить значения k для каждого вектора

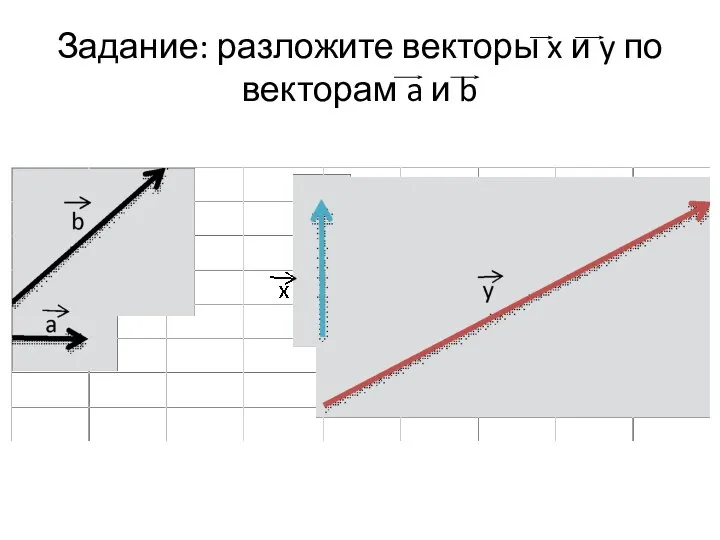
Задание: разложите векторы x и y по векторам a и b

Координаты вектора

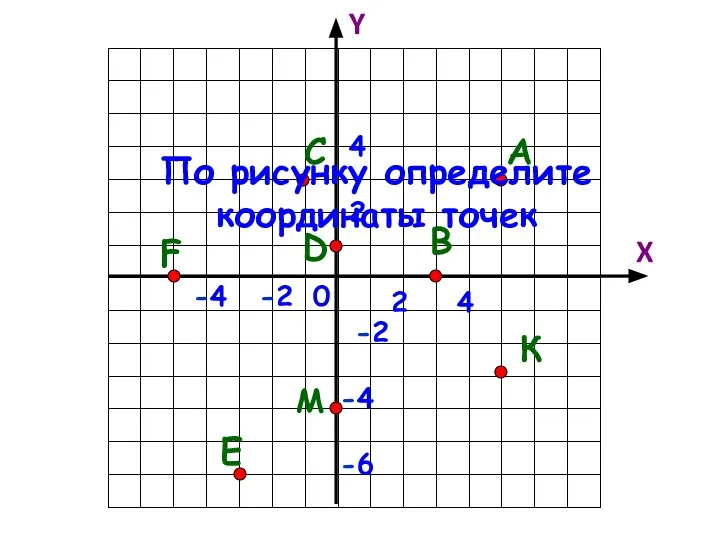
По рисунку определите координаты точек
М

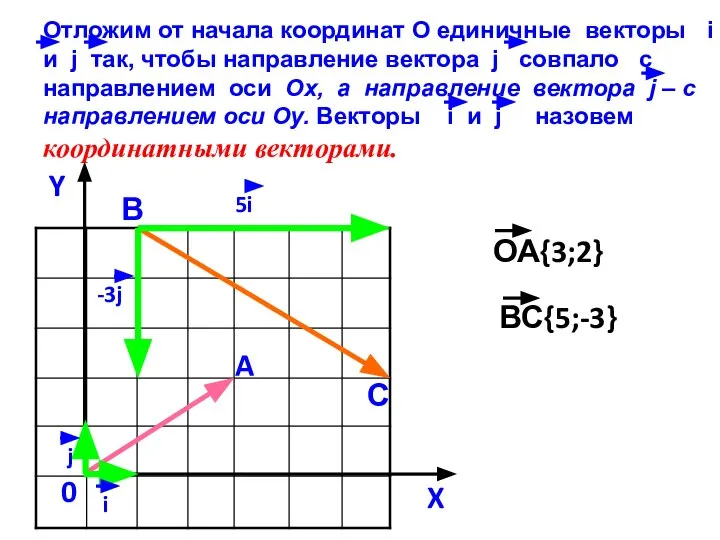
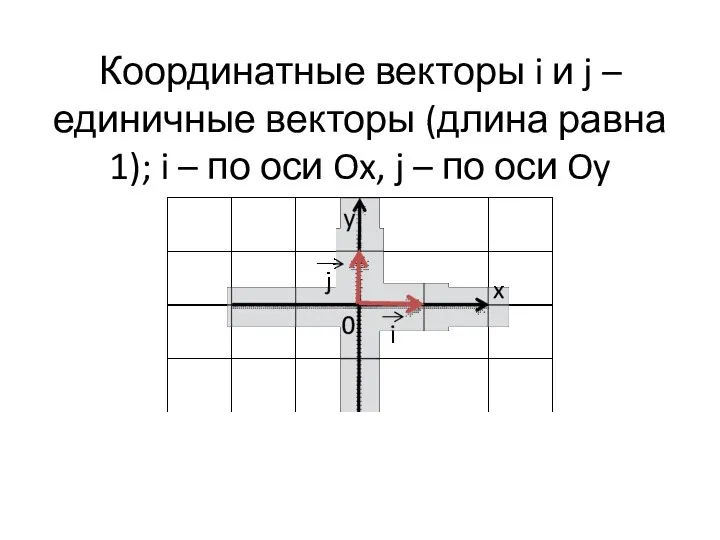
Координатные векторы i и j – единичные векторы (длина равна 1); i – по оси Ox, j – по оси Oy

ОА{3;2}
В
ВС{5;-3}

Любой вектор можно разложить по координатным векторам

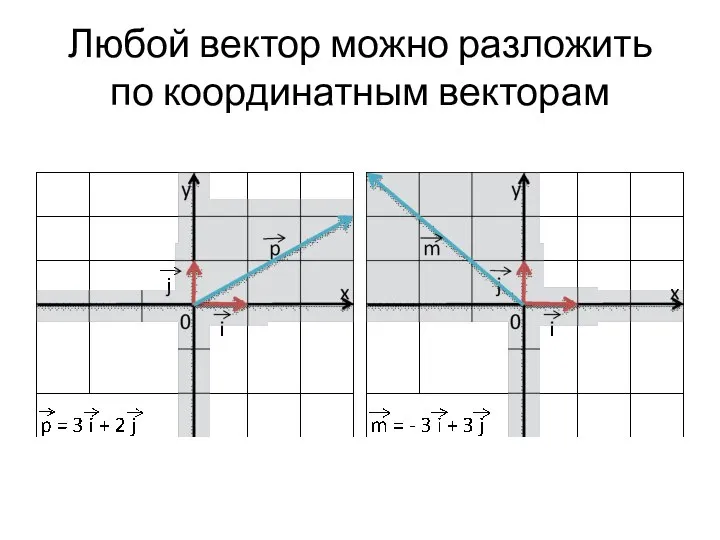
Коэффициенты разложения называются координатами вектора

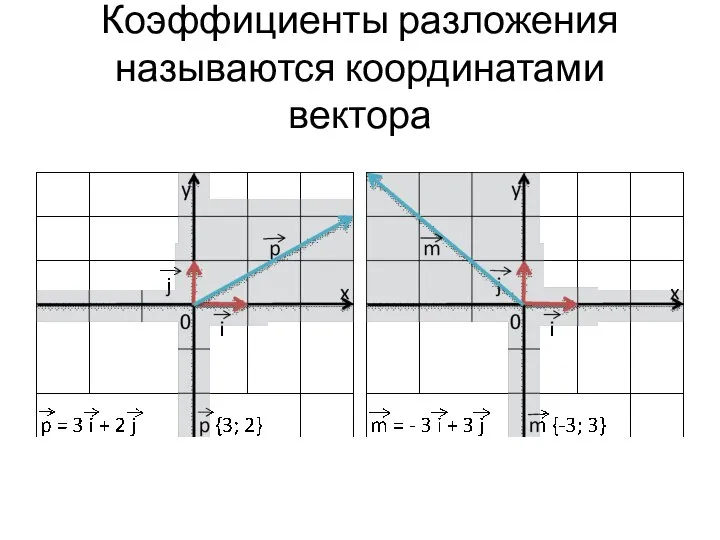
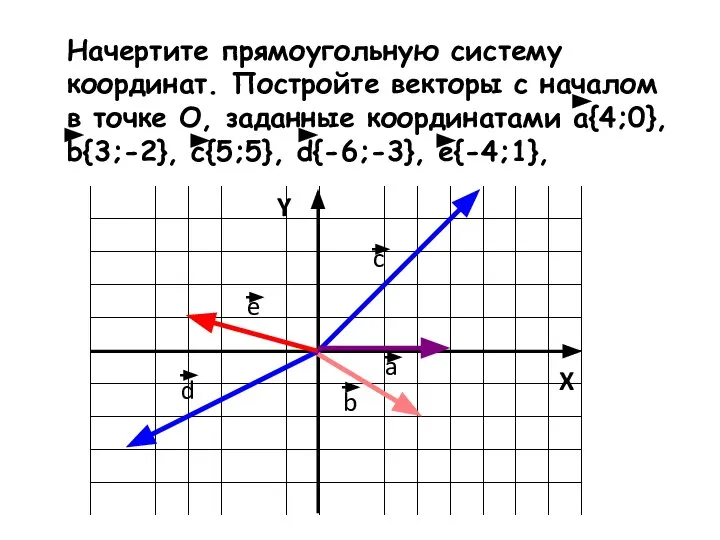
Начертите прямоугольную систему координат. Постройте векторы с началом в точке О, заданные координатами a{4;0}, b{3;-2}, c{5;5}, d{-6;-3}, e{-4;1},

1. Каждая координата суммы векторов равна сумме соответствующих координат
a {2;3} + b {1;4} = c {3;7}
2. Каждая координата разности векторов равна разности соответствующих координат
a {2;3} - b {1;4} = c {1;-1}

3. Каждая координата произведения вектора на число равна произведению соответствующей координаты на это число
если a {2;5}, то -4 a {-8;-20}