Содержание
- 2. Дифференциальным уравнением (ДУ) называется уравнение, содержащее производные от искомой функции или её дифференциалы. или
- 3. Примеры ДУ:
- 4. Наивысший порядок производной, входящей в уравнение, называется порядком ДУ. Решением ДУ называется такая функция, подстановка которой
- 5. Пример: Показать, что данная функция является решением ДУ Т.о. функции вида являются решениями данного ДУ при
- 6. Дифференциальные уравнения I порядка
- 7. Общим решением ДУ I порядка называется функция , которая зависит от одного произвольного постоянного С. или
- 8. Частным решением ДУ I порядка называется любая функция полученная из общего решения при конкретном значении постоянной
- 9. Пример: ДУ: -общее решение частные решения
- 10. Геометрически: Общее решение ДУ есть семейство интегральных кривых на плоскости Оху; Частное решение ДУ -одна кривая
- 11. Задача отыскания конкретного частного решения данного ДУ по начальным данным называется задачей Коши (Cauchy). или Условие
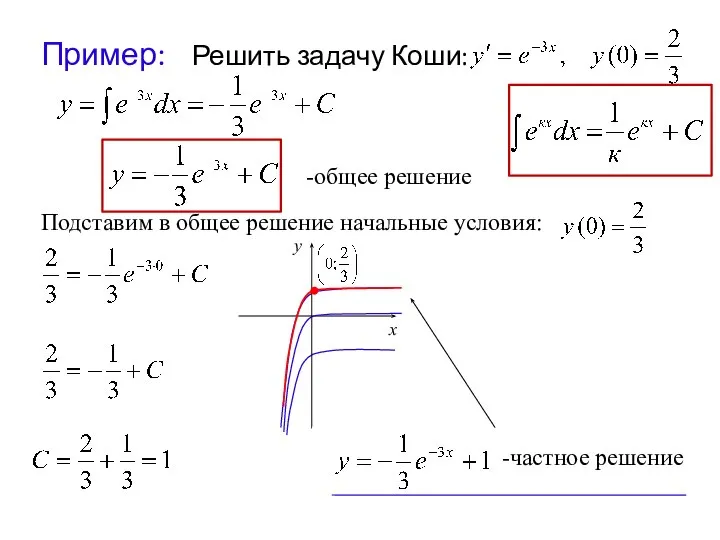
- 12. Пример: Решить задачу Коши: -общее решение Подставим в общее решение начальные условия: -частное решение х у
- 13. 1. ДУ I порядка с разделёнными переменными Если каждая часть ДУ представляет собой произведение некоторого выражения,
- 14. Пример: Решить ДУ С общее решение: или Геометрически: получили семейство концентрических окружностей с центром в начале
- 15. 2. ДУ I порядка с разделяющимися переменными Уравнения, в которых переменные разделяются, называются ДУ с разделяющимися
- 16. Пример: Найти общее и частное решение ДУ ⇒
- 17. Итак, общее решение ДУ: 2) Найдём частное решение ДУ, если Подставим эти начальные условия в общее
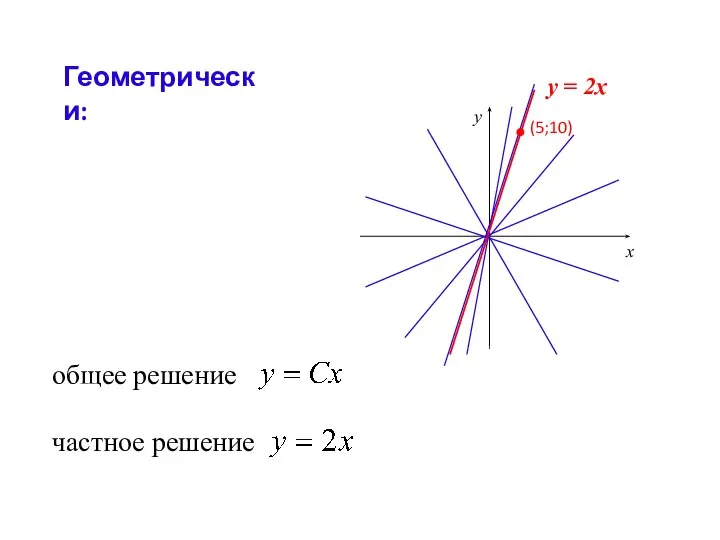
- 18. Геометрически: х у общее решение частное решение у = 2х (5;10)
- 19. Пример: Решить задачу Коши
- 21. Скачать презентацию
















 Уравнения и неравенства
Уравнения и неравенства Примеры на состав числа 6
Примеры на состав числа 6 Простейшие преобразования графиков функцмй
Простейшие преобразования графиков функцмй Личные местоимения
Личные местоимения Теория вероятностей. Примеры решения задач. Задачи
Теория вероятностей. Примеры решения задач. Задачи Показательная функция, её свойства и график. Логарифмическая функция, ее свойства и график
Показательная функция, её свойства и график. Логарифмическая функция, ее свойства и график Свойства уравнения
Свойства уравнения Урок математики в 10 классе по теме Пирамида
Урок математики в 10 классе по теме Пирамида Функции одной переменной (лекция № 1)
Функции одной переменной (лекция № 1) Показательная функция. Теория
Показательная функция. Теория Загадки и тайны треугольника
Загадки и тайны треугольника Основы геометрии (5 класс)
Основы геометрии (5 класс) Vaths. Properties of Shapes
Vaths. Properties of Shapes Параллельное проектирование
Параллельное проектирование Школа скорочтения и развития интеллекта IQ007. Ментальная арифметика
Школа скорочтения и развития интеллекта IQ007. Ментальная арифметика Концентрация. Часть II
Концентрация. Часть II Центральная симметрия. Осевая симметрия
Центральная симметрия. Осевая симметрия Решение задач. 2 класс
Решение задач. 2 класс Основные тригонометрические формулы
Основные тригонометрические формулы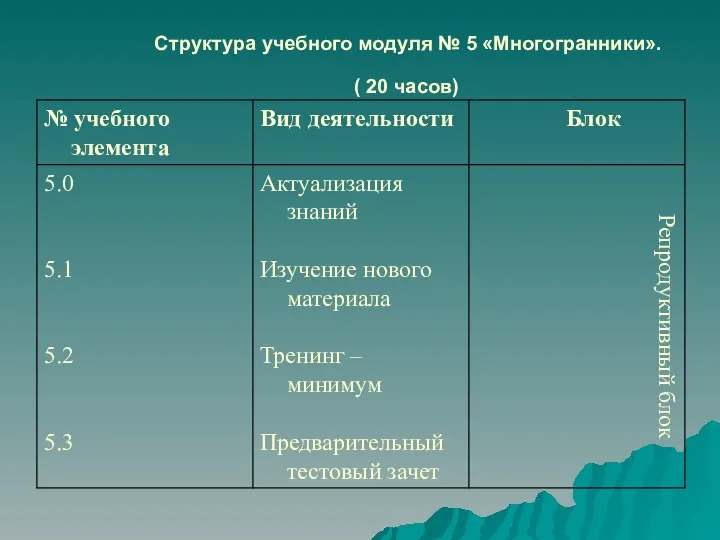 Структура учебного модуля № 5 Многогранники. ( 20 часов)
Структура учебного модуля № 5 Многогранники. ( 20 часов) Презентация на тему Начальные понятия планиметрии. Прямая и отрезок. Луч и угол
Презентация на тему Начальные понятия планиметрии. Прямая и отрезок. Луч и угол  Пирамида. Площади поверхностей. Объём. Многогранники
Пирамида. Площади поверхностей. Объём. Многогранники Анализ вариационных рядов, показатели дифференциации и концентрации
Анализ вариационных рядов, показатели дифференциации и концентрации Логарифмические уравнения
Логарифмические уравнения Цифра 8
Цифра 8 Числовая окружность
Числовая окружность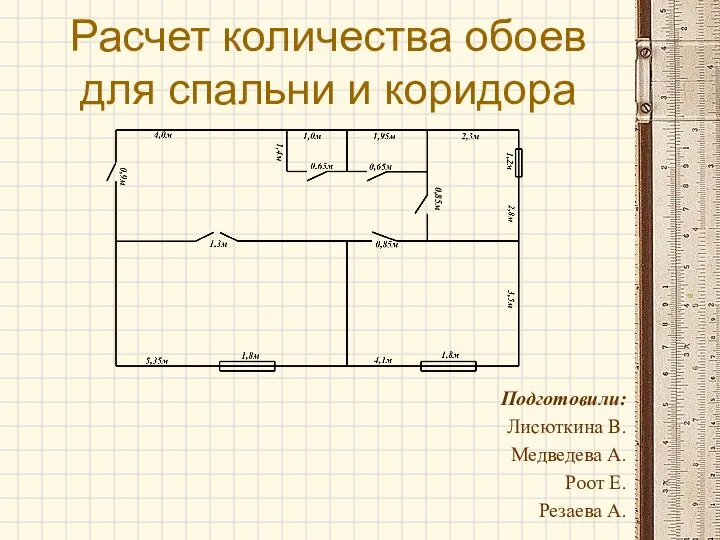 Расчет количества обоев для спальни и коридора
Расчет количества обоев для спальни и коридора Определение длин контррельсов и усовиков
Определение длин контррельсов и усовиков