Содержание
- 2. Комбинаторика- это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или
- 3. Комбинаторика необходима: -конструктору, разрабатывающему новую модель механизма; -механику, занимающемуся сложными сооружениями; -ученому-агроному, планирующему распределение сельхозкультур на
- 4. Исторические корни Комбинаторика возникла в глубокой древности, много тысячелетий назад
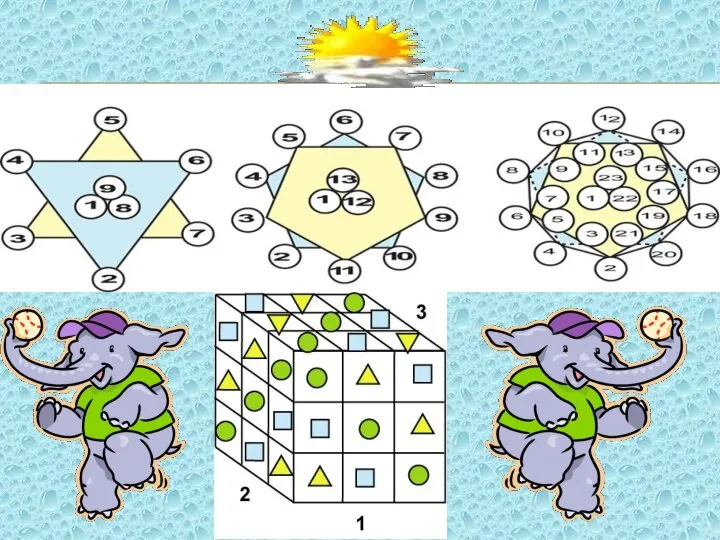
- 5. Древний Китай Составление магических квадратов (Заданные числа располагали так, что их сумма по всем горизонталям, вертикалям
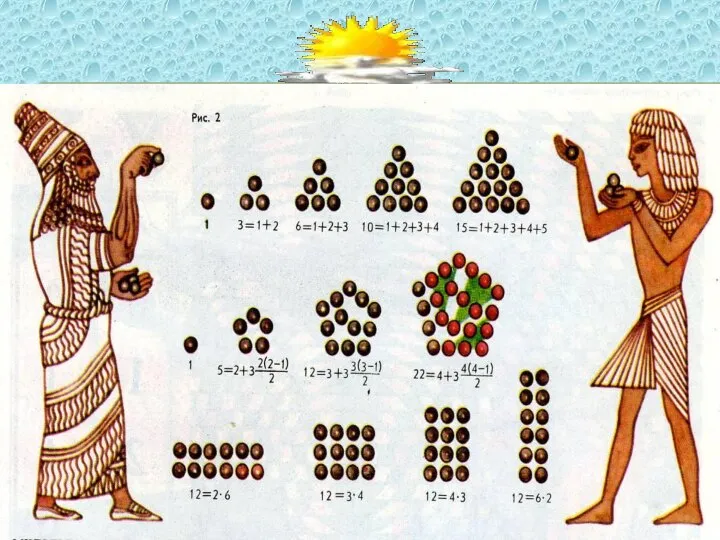
- 7. Древняя Греция -Подсчитали , что число различных комбинаций длинных и коротких слогов в стихотворных размерах; -занимались
- 9. 17 в.- период возникновения теории вероятностей. Комбинаторика становится наукой.
- 10. Пионеры комбинаторики: Итальянские ученые- Дж. Кардано, Н.Тартальей, Г.Галиллей(16в.) Французские ученые- Б.Паскаль, П.Ферма(16в.) Немецкий ученый- Г.Лейбниц(17в.) Швейцарский
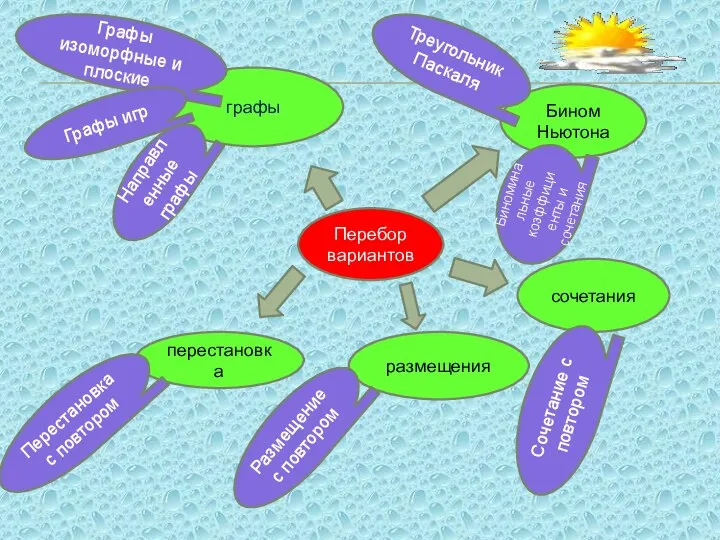
- 11. Основные типы задач комбинаторики
- 12. Перебор вариантов сочетания Бином Ньютона размещения перестановка графы Графы изоморфные и плоские Графы игр Направленные графы
- 13. Задача о квартете В знаменитой басне Крылова «Квартет» «Проказница мартышка, Осел, Козел да косолапый Мишка» исследовали
- 15. Решение: 1 способ- в ряд Здесь n=4, поэтому способов «усесться чинно в ряд» имеется P =
- 16. 2 способ- по кругу Пронумеруем всех участников по часовой стрелке, начиная скажем с Осла! В различных
- 17. Задача о паспортах. Воспетый Маяковским «молоткастый, серпастый» советский паспорт имел серию и номер, состоящие в общей
- 18. Решение: Римские цифры серии зафиксируем. Остаются две русские буквы и шесть арабских цифр. Буквы В русском
- 19. Задача о лото – миллион Нужно угадать из 49 номеров 6, которые выпадут во время тиража.
- 21. Решение: Сколько карточек нужно купить и заполнить, чтобы на них оказались все возможные комбинации по 6
- 23. Скачать презентацию

















 Презентация на тему ТОЧКИ И ЛИНИИ. ПРЯМАЯ
Презентация на тему ТОЧКИ И ЛИНИИ. ПРЯМАЯ  Градусное измерение углов. Сумма углов в треугольнике. Тест
Градусное измерение углов. Сумма углов в треугольнике. Тест Решение линейных систем уравнений способом подстановки
Решение линейных систем уравнений способом подстановки Контрольная работа. Логарифм, логарифмическая функция
Контрольная работа. Логарифм, логарифмическая функция Свойства и графики тригонометрических функций
Свойства и графики тригонометрических функций Шахматные головоломки. Для любителей логических задач
Шахматные головоломки. Для любителей логических задач Решение квадратных уравнений
Решение квадратных уравнений Определение равнодействующей и уравновешивающих сходящихся сил плоской системы сил графическим и аналитическим способами
Определение равнодействующей и уравновешивающих сходящихся сил плоской системы сил графическим и аналитическим способами Рассчитать площадь и периметр прямоугольника по двум известным сторонам. Алгоритм решения подобных задач
Рассчитать площадь и периметр прямоугольника по двум известным сторонам. Алгоритм решения подобных задач Углы, связанные с окружностью
Углы, связанные с окружностью Весенняя прогулка. Занятие по математике для детей средней группы с ТНР
Весенняя прогулка. Занятие по математике для детей средней группы с ТНР Учение – это сила. Зимняя математическая олимпиада
Учение – это сила. Зимняя математическая олимпиада Электронное приложение к рабочей тетради по математике 1 класс школа VIII вида дочисловой период
Электронное приложение к рабочей тетради по математике 1 класс школа VIII вида дочисловой период Квадрат. Прямоугольник
Квадрат. Прямоугольник Геометрия
Геометрия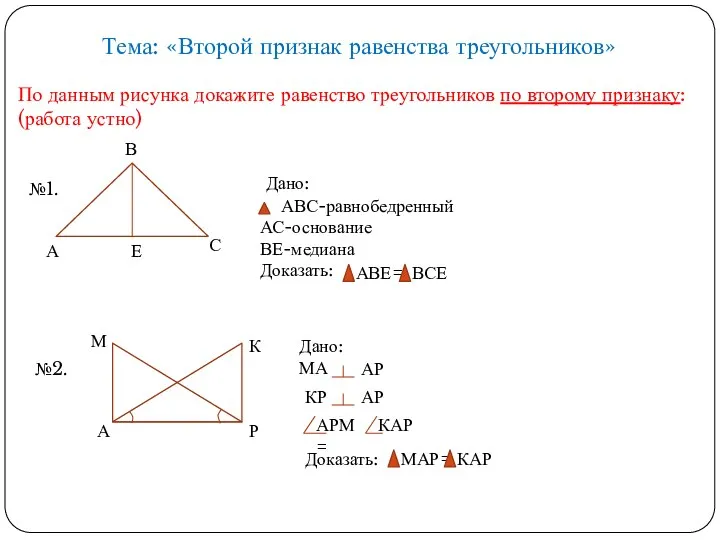 Равенство треугольников по второму признаку
Равенство треугольников по второму признаку Признаки параллельности прямых
Признаки параллельности прямых Решение задач в целых числах
Решение задач в целых числах ЕГЭ. Решение задач
ЕГЭ. Решение задач Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Решение текстовых задач
Решение текстовых задач Второй и третий признаки равенства треугольников. LOGO
Второй и третий признаки равенства треугольников. LOGO Системы счисления
Системы счисления Презентация на тему Внетабличное умножение и деление
Презентация на тему Внетабличное умножение и деление  Признаки параллельности прямых
Признаки параллельности прямых Понятие о задачах математической статистики
Понятие о задачах математической статистики Вероятность события
Вероятность события Сумма углов треугольника
Сумма углов треугольника