Конус

Оглавление
Свойства
Развертка
Усеченный конус

Свойства конуса
Объем конуса равен одной третьей от произведения основания на высоту
S=1/3(S*H)
Если разрезать конус по любой из образующих мы получим развертку конуса-сектор.

Площадь боковой поверхности конуса равна будет равна площади сектора радиусом R
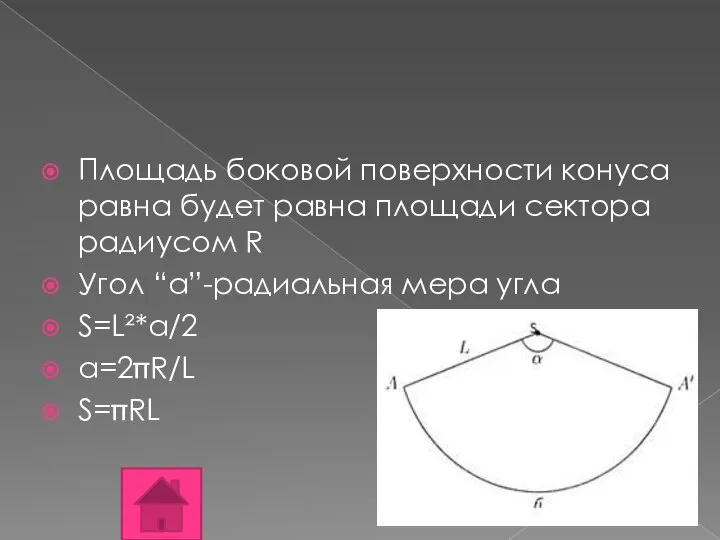
Угол “а”-радиальная мера угла
S=L²*a/2
a=2R/L
S=RL

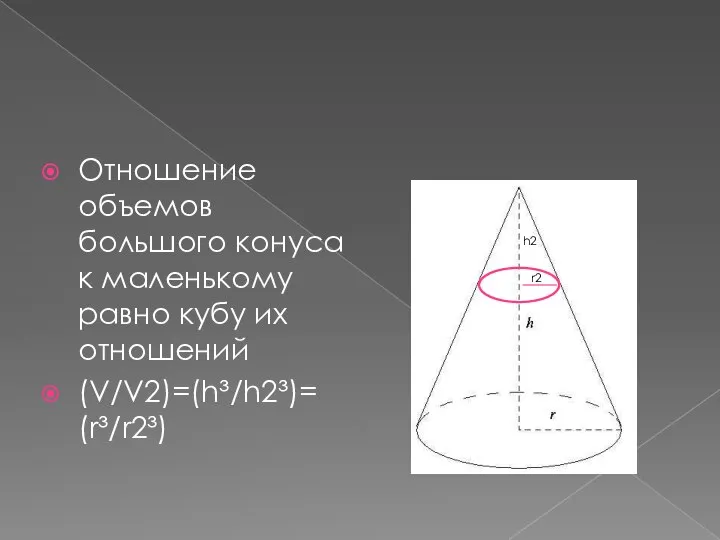
Отношение объемов большого конуса к маленькому равно кубу их отношений
(V/V2)=(h³/h2³)= (r³/r2³)
r2
h2

Развертка
Прямой круговой конус как тело вращения образован прямоугольным треугольником, вращающимся вокруг одного из катетов, гдеh — высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольника r — радиус в основании конуса. Гипотенузой прямоугольного треугольника является l — образующая конуса.

В создании развёртки конуса могут использоваться всего две величины r и l. Радиус основания r определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхности l, являющаяся радиусом сектора боковой поверхности. Угол сектора в развёртке боковой поверхности конуса определяется по формуле:
φ = 360°·(r/l).

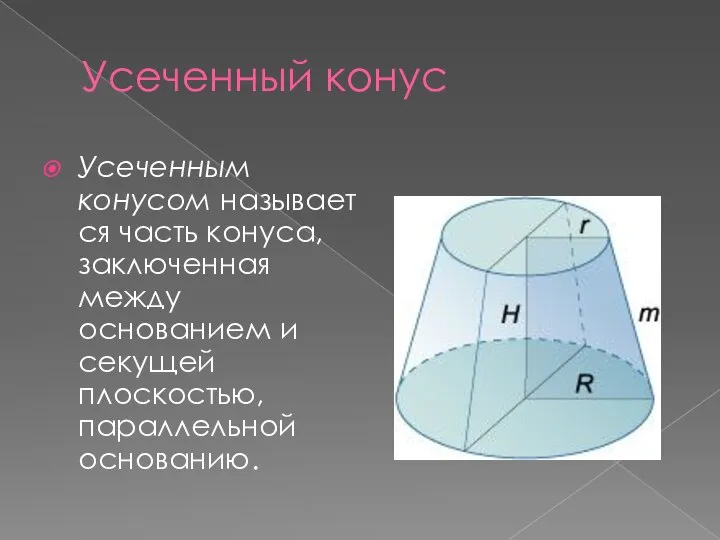
Усеченный конус
Усеченным конусом называется часть конуса, заключенная между основанием и секущей плоскостью, параллельной основанию.

Площадь боковой поверхности усеченного конуса
Sбок =πm(R+r)
Отношение площадей нижнего и верхнего оснований
S2/S1=R²/r²=k²,
где k − коэффициент подобия.