Содержание
- 2. Назвать функции, заданные формулами и соответствующие им графики.
- 3. Свойства функции: область определения функции область значений функции четность функции возрастание (убывает) функции наибольшее и наименьшее
- 4. Определение: Логарифмом положительного числа b по основанию а, где а>0, а≠1, называется показатель степени, в которую
- 5. Записаны формулы, определите, какие из них записаны неверно:
- 6. Самостоятельная работа Вычислите: 1 вариант. 2 вариант.
- 7. Проверка: Ответы:1 вариант: -2;-1;0;1;2;3; нет. Ответы:2 вариант: 2;1;0;-1;-2;-3; нет.
- 8. Итак, мы повторили необходимый материал. С какими трудностями вы встретились при выполнении самостоятельной работы?
- 9. Вернемся к заданиям самостоятельной работы на повторение понятия логарифма. Задание. Обозначьте изменяющуюся величину через x. При
- 10. Задаются ли этими формулами функции?... Объясните, почему? Посмотрите внимательно на правую часть формулы. Подумайте, как бы
- 11. Тема урока:
- 12. Тема урока: «Логарифмическая функция, её свойства и график».
- 13. Цели урока. Ввести понятие логарифмической функции, дать определение. Изучить основные свойства логарифмической функции. Сформировать умение выполнять
- 14. Постройте графики функций по вариантам используя результаты самостоятельной работы I вариант II вариант
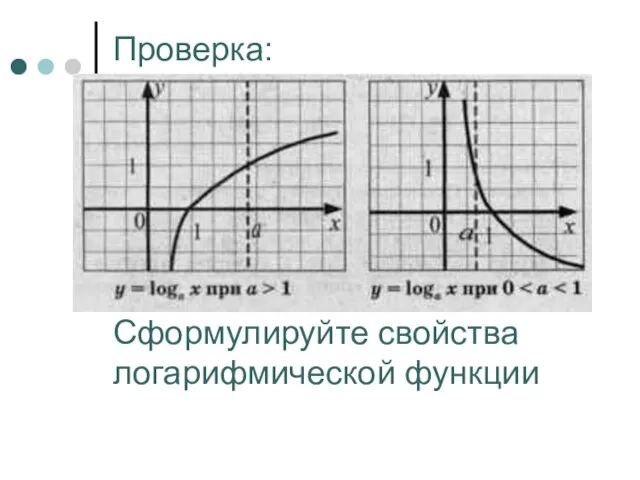
- 15. Проверка: Сформулируйте свойства логарифмической функции
- 16. Свойства логарифмической функции. область определения - множество всех положительных чисел (х>0). область значений - множество всех
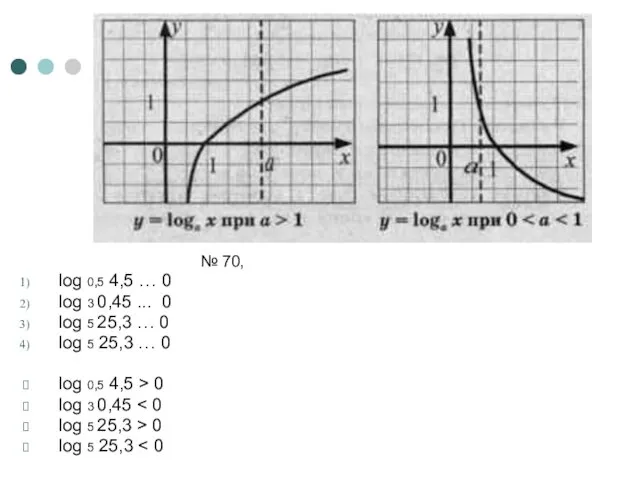
- 17. Закрепление нового материала. Стр 243, № 69 Объясните, как при сравнении значений логарифмов, вы будете использовать
- 18. № 70, log 0,5 4,5 … 0 log 3 0,45 ... 0 log 5 25,3 …
- 19. Задание. Постройте график функции
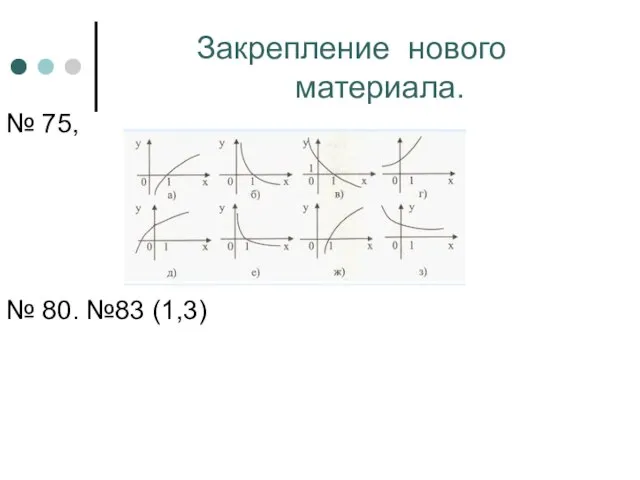
- 20. Закрепление нового материала. № 75, № 80. №83 (1,3)
- 21. В математике встречаются немного экзотические графики. Одним из них является логарифмическая спираль.
- 22. ПРЕЗЕНТАЦИЯ НА ТЕМУ «ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ» Презентацию выполнил ученик 10 «А» Максим Щетков
- 23. В математике встречаются немного экзотические графики. Одним из них является логарифмическая спираль. Спираль имеет бесконечное множество
- 24. Уравнение логарифмической спирали Логарифмическая спираль описывается уравнением r=aф, где r – расстояние от точки, вокруг которой
- 25. Свойства логарифмической спирали Произвольный луч, выходящий из полюса спирали, пересекает любой виток спирали под одним и
- 26. Свойства логарифмической спирали Если вращать спираль вокруг полюса по часовой стрелке, то можно наблюдать кажущееся растяжение
- 27. Логарифмическая спираль в природе Один из наиболее распространенных пауков, эпейра, сплетая паутину, закручивает нити вокруг центра
- 28. Живые существа обычно растут, сохраняя общее очертание своей формы. При этом они растут чаще всего во
- 29. Можно сказать, что эта спираль является математическим символом соотношения форм роста. Великий немецкий поэт Иоганн Вольфганг
- 31. Скачать презентацию

























 Введение таблицы умножения (Школа XXI века. Рудницкая В.Н )
Введение таблицы умножения (Школа XXI века. Рудницкая В.Н ) Что такое степень
Что такое степень Презентация на тему Уравнения в ЕГЭ по математике: примеры и решения
Презентация на тему Уравнения в ЕГЭ по математике: примеры и решения  Подобие треугольников. Первый признак подобия
Подобие треугольников. Первый признак подобия Обыкновенные дроби
Обыкновенные дроби Делители числа
Делители числа Граф. Построение графов
Граф. Построение графов Проценты. Часть 2
Проценты. Часть 2 Преобразование тригонометрических выражений
Преобразование тригонометрических выражений Целые и дробные числа
Целые и дробные числа Презентация на тему Умножение и деление степеней
Презентация на тему Умножение и деление степеней 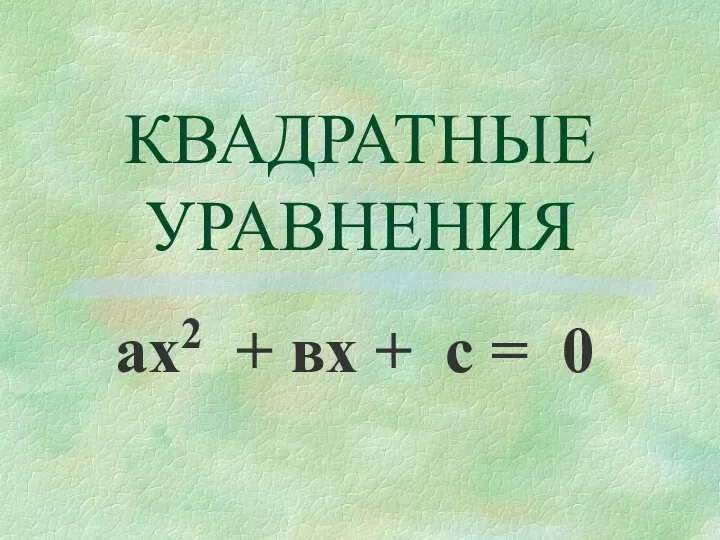 Квадратные уравнения ах2 + вх + с = 0
Квадратные уравнения ах2 + вх + с = 0 Окружность и круг
Окружность и круг Методы оценки рисков проекта
Методы оценки рисков проекта Математика. Задания на лето. Часть 3
Математика. Задания на лето. Часть 3 определение и свойства числ.функции
определение и свойства числ.функции Подготовка к контрольной работе
Подготовка к контрольной работе Геометрия пчелиных сот
Геометрия пчелиных сот Понятие процента
Понятие процента Проверка статистических гипотез. Статистическая функция распределения случайной величины
Проверка статистических гипотез. Статистическая функция распределения случайной величины Смотр знаний: Экскурс по формулам сокращенного умножения
Смотр знаний: Экскурс по формулам сокращенного умножения Состав числа 5
Состав числа 5 Решение задач. Параллельные прямые
Решение задач. Параллельные прямые Презентация на тему Викторина "Ох уж эта математика" 5 класс
Презентация на тему Викторина "Ох уж эта математика" 5 класс  Выборочное наблюдение. Практическое занятие
Выборочное наблюдение. Практическое занятие График показательной функции
График показательной функции Комбинаторика. Правило умножения
Комбинаторика. Правило умножения Окружность и круг
Окружность и круг