Слайд 2Определение.
Уравнения, в которых под знаком корня содержится переменная, называют иррациональными.
Примеры:

Слайд 3Методы решения иррациональных уравнений.
1.
Если а - отрицательно, то уравнение
- не

имеет решения;
Если то уравнение
Это следует из определения арифметического корня.
Слайд 5Решите самостоятельно
Решение: Возведем обе части в квадрат.
Ответ: 2; -3.

Слайд 62. Решение иррациональных уравнений, используя переход к смешанной системе.

Слайд 7Пример:
удовлетворяет условию
не удовлетворяет
условию
Ответ: посторонний корень.

Слайд 8Решите самостоятельно.
Решение:
удовлетворяет условию
не удовлетворяет условию -
посторонний корень. Ответ:

Слайд 93. Переход к равносильной системе.

Слайд 10Пример.
удовлетворяет условию удовлетворяет условию

Слайд 11Решите самостоятельно
Решение:
Ответ:

Слайд 124.
Если , то не имеет
решения.
Если , то

Слайд 13Пример:
- не
удовлетворяет
условию
- удовлетворяет
условию
Ответ:













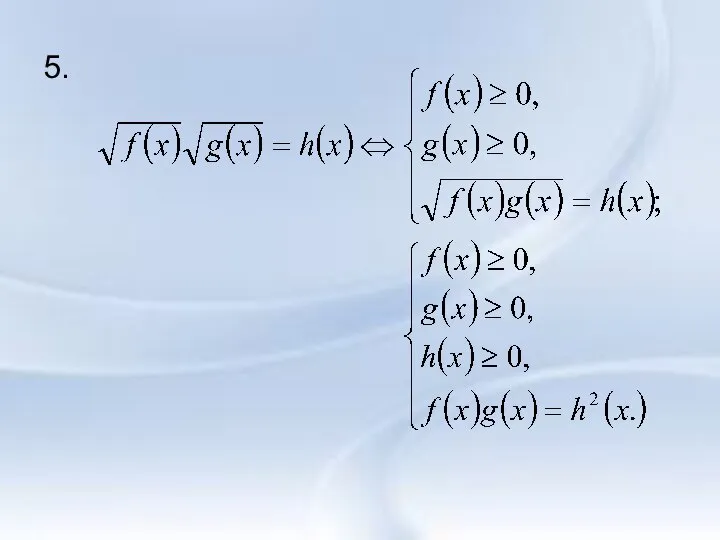

 Система пропорционирования в проектировании объектов дизайна
Система пропорционирования в проектировании объектов дизайна Кроссворд Геометрические термины
Кроссворд Геометрические термины Виды задач на вступительной работе для поступления в математическую вертикаль
Виды задач на вступительной работе для поступления в математическую вертикаль Скалярное произведение векторов
Скалярное произведение векторов Проценты. Ж.Ж. Руссо (1712–1778 гг.)
Проценты. Ж.Ж. Руссо (1712–1778 гг.) Методы интегрирования
Методы интегрирования Равнобедренный треугольник
Равнобедренный треугольник Презентация по математике "Отношение больше, меньше" -
Презентация по математике "Отношение больше, меньше" -  Путешествие по математическому морю (2)
Путешествие по математическому морю (2) Определите, какими являются данные величины: прямо пропорциональными, обратно пропорциональными или ни теми ни другими
Определите, какими являются данные величины: прямо пропорциональными, обратно пропорциональными или ни теми ни другими Плоское зеркало. Построение изображений в плоском зеркале
Плоское зеркало. Построение изображений в плоском зеркале Задачи. вариант 3
Задачи. вариант 3 Стереометрия. Геометрия
Стереометрия. Геометрия Системы уравнений первой и второй степени
Системы уравнений первой и второй степени Анализ и синтез как методы научного познания, их применение при обучении математике
Анализ и синтез как методы научного познания, их применение при обучении математике Теорема Пифагора
Теорема Пифагора Простейшие тригонометрические неравенства и методы их решения
Простейшие тригонометрические неравенства и методы их решения Решение задач
Решение задач Презентация на тему Элементы теории вероятностей на ЕГЭ
Презентация на тему Элементы теории вероятностей на ЕГЭ  Мнимые числа. Определение комплексных чисел
Мнимые числа. Определение комплексных чисел Тест по теме: Углы. Параллельные прямые. Перпендикулярные прямые
Тест по теме: Углы. Параллельные прямые. Перпендикулярные прямые Презентация на тему Алгебраические уравнения произвольных степеней 10 класс
Презентация на тему Алгебраические уравнения произвольных степеней 10 класс  Многоугольники
Многоугольники Решение уравнений
Решение уравнений Построение плана изучения чисел
Построение плана изучения чисел Математика. 3 класс
Математика. 3 класс Численные методы (траектория 1)
Численные методы (траектория 1) Ряды. Лекция
Ряды. Лекция