Слайд 2Параметр в уравнении или неравенстве некоторая плавающая величина, т.е. число, принимающая различные

значения
Уравнение с параметрами — математическое уравнение внешний вид и решение которого зависит от значений одного или нескольких параметров.
Решить уравнение с параметром означает, что нужно найти все системы значений параметров, при которых выполняется то или иное требование.
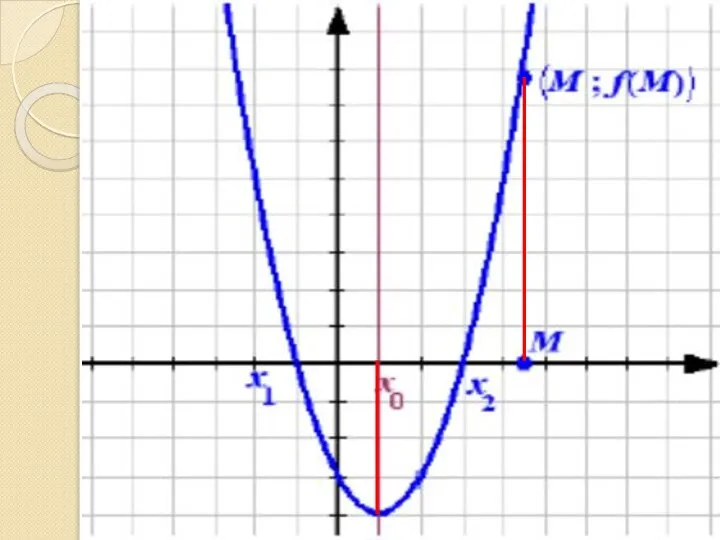
Слайд 3При каких условиях корни уравнения
меньше числа М?
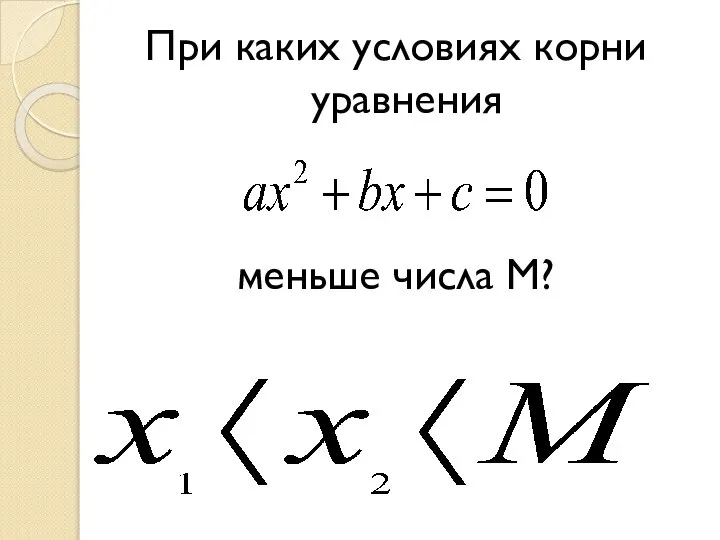
Слайд 4Рассмотрим соответствующую квадратичную функцию
Найдем вершину параболы

Слайд 5 I случай
Ветви параболы направлены вверх
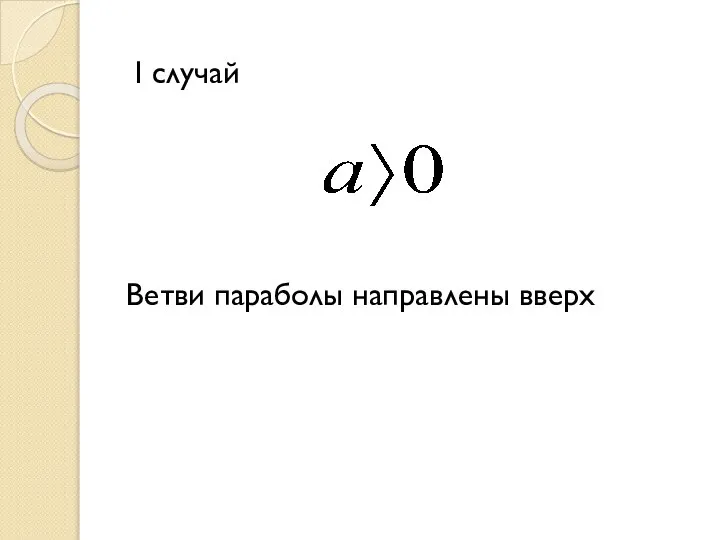
Слайд 6Условие существования действительных корней квадратного уравнения

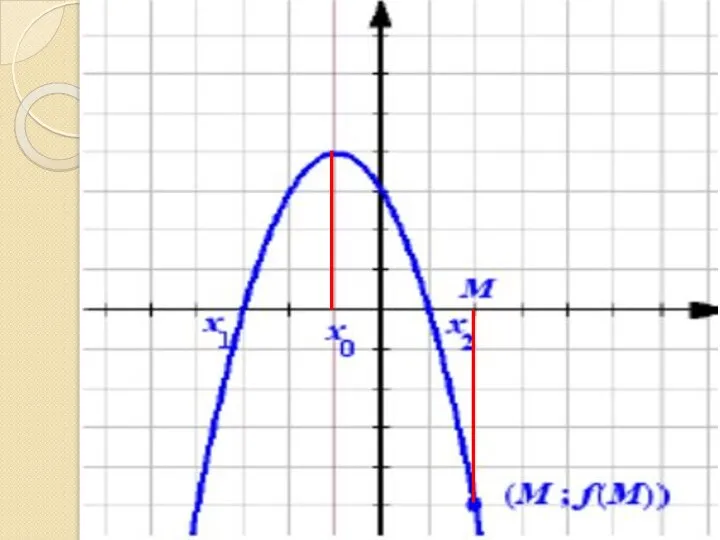
Слайд 9 II случай
Ветви параболы направлены вниз

Слайд 13При каких значениях параметра m корни уравнения
отрицательны.

Слайд 17При каких значениях параметра р корни уравнения
1 группа
меньше 0.
2 группа
меньше -1
3

группа
меньше 1
Слайд 19
При каких условиях корни уравнения
больше числа М?


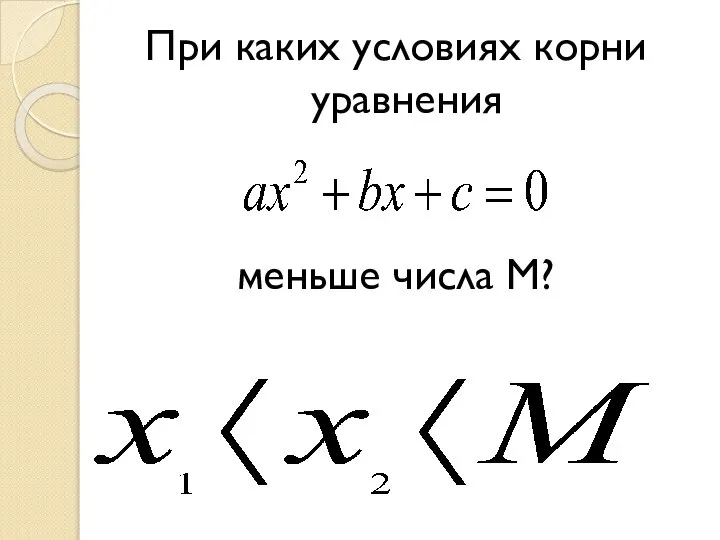

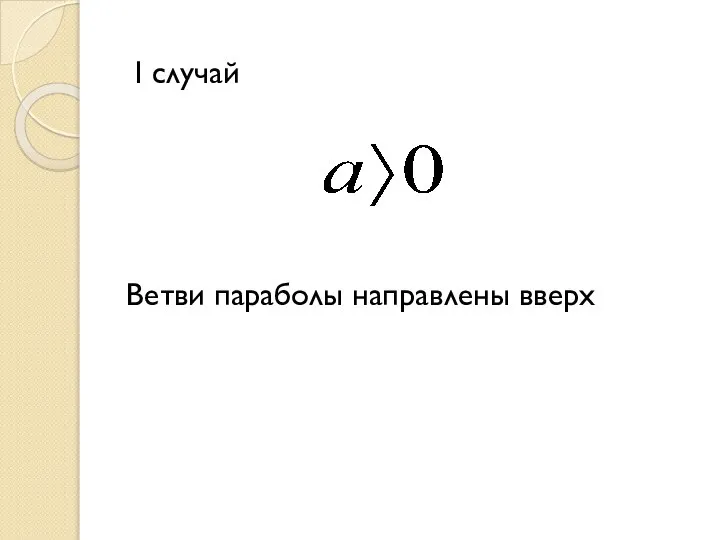

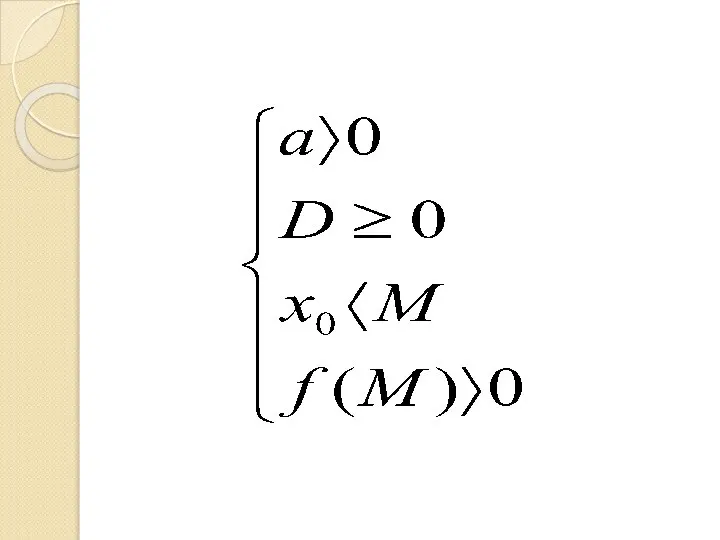

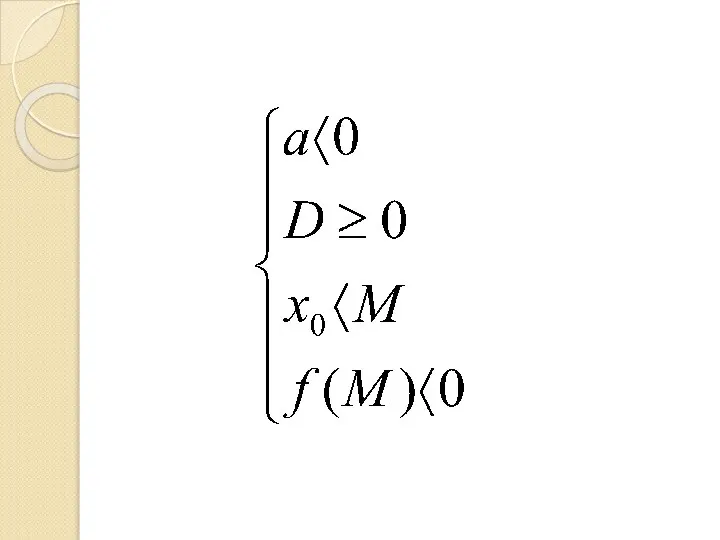

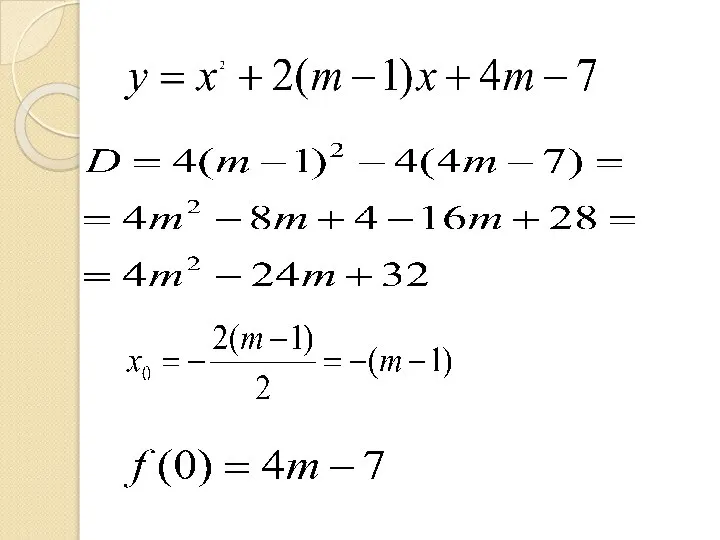
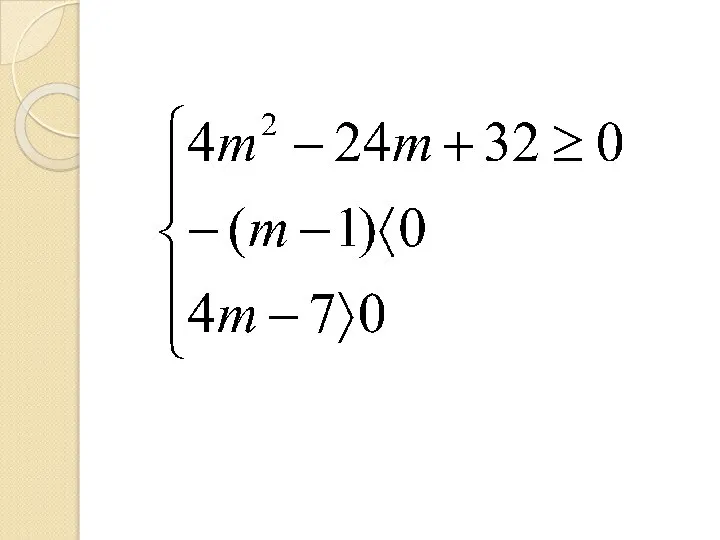
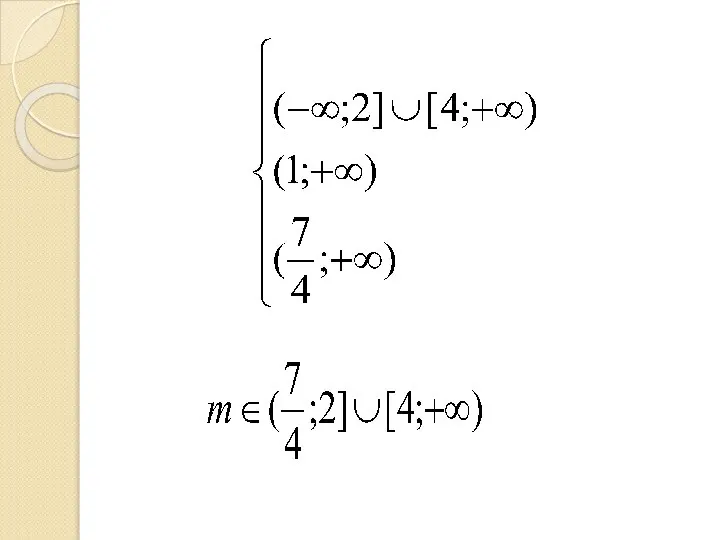



 Квадратный корень из степени
Квадратный корень из степени Определение свойств функции по графику
Определение свойств функции по графику Параллельные прямые, перпендикулярные к плоскости
Параллельные прямые, перпендикулярные к плоскости Основы математической статистики. Регрессионный и корреляционный анализы
Основы математической статистики. Регрессионный и корреляционный анализы Задача о кратчайшем пути
Задача о кратчайшем пути Развертка. Создание объёмных фигур из плоскости
Развертка. Создание объёмных фигур из плоскости Перетворення графіків
Перетворення графіків Идеально сбалансированное дерево. Задание
Идеально сбалансированное дерево. Задание Больше, меньше, столько же
Больше, меньше, столько же Геометрические тела. Обьём прямоугольного параллелепипеда. 5 класс
Геометрические тела. Обьём прямоугольного параллелепипеда. 5 класс Формирование действия моделирования через решение текстовых задач
Формирование действия моделирования через решение текстовых задач Уравнение окружности и прямой
Уравнение окружности и прямой Мир чисел
Мир чисел Симмертия. Зеркальное отражение – симметрия
Симмертия. Зеркальное отражение – симметрия Деление дробей
Деление дробей Соста числа 11
Соста числа 11 Деление десятичных дробей
Деление десятичных дробей Квадрат. Основные свойства квадрата
Квадрат. Основные свойства квадрата Сравнение и измерение отрезков
Сравнение и измерение отрезков Стандартный вид одночлена
Стандартный вид одночлена Презентация на тему Решение иррациональных неравенств (11 класс)
Презентация на тему Решение иррациональных неравенств (11 класс)  Презентация на тему КВАДРАТИЧНАЯ ФУНКЦИЯ И КВАДРАТИЧНЫЕ НЕРАВЕНСТВА
Презентация на тему КВАДРАТИЧНАЯ ФУНКЦИЯ И КВАДРАТИЧНЫЕ НЕРАВЕНСТВА  Домашнее задание по геометрии
Домашнее задание по геометрии Количество делителей числа
Количество делителей числа Комплексные числа
Комплексные числа Цифра 1. Посчитаем до 10
Цифра 1. Посчитаем до 10 Презентация по математике "Алгоритмы внутренних точек с приближенным решением вспомогательной задачи" -
Презентация по математике "Алгоритмы внутренних точек с приближенным решением вспомогательной задачи" -  Algorytmy i struktury danych
Algorytmy i struktury danych