Содержание
- 2. Понятие числовой последовательности Рассмотрим ряд натуральных чисел N: 1, 2, 3, …, n – 1, n,
- 3. Примеры числовых последовательностей 1, 2, 3, 4, 5, … – ряд натуральных чисел; 2, 4, 6,
- 4. Способы задания последовательностей Перечислением членов последовательности (словесно). Заданием аналитической формулы. Заданием рекуррентной формулы. Примеры: Последовательность простых
- 5. Ограниченность числовой последовательности Последовательность {уn} называют ограниченной сверху, если все ее члены не больше некоторого числа.
- 6. Ограниченность числовой последовательности Последовательность {уn} называют ограниченной снизу, если все ее члены не меньше некоторого числа.
- 7. Возрастание и убывание числовой последовательности Последовательность {уn} называют возрастающей последовательностью, если каждый ее член больше предыдущего:
- 8. Предел числовой последовательности Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу a при увеличении
- 9. Предел числовой последовательности Это определение означает, что a есть предел числовой последовательности, если её общий член
- 10. Рассмотрим последовательность: – гармонический ряд Если │q│ Если │q│> 1, то последовательность уn = q n
- 11. Основные теоремы о пределах Теорема 1. Функция не может иметь более одного предела. Теорема 2. Предел
- 12. Основные теоремы о пределах Следствие 2. Предел степени равен степени предела, т.е. Теорема 4. Предел частного
- 13. Если m∈N, k∈R, то
- 14. Примеры:
- 15. Предел функции на бесконечности В этом случае прямая у=b является горизонтальной асимптотой графика функции y=f(x). х
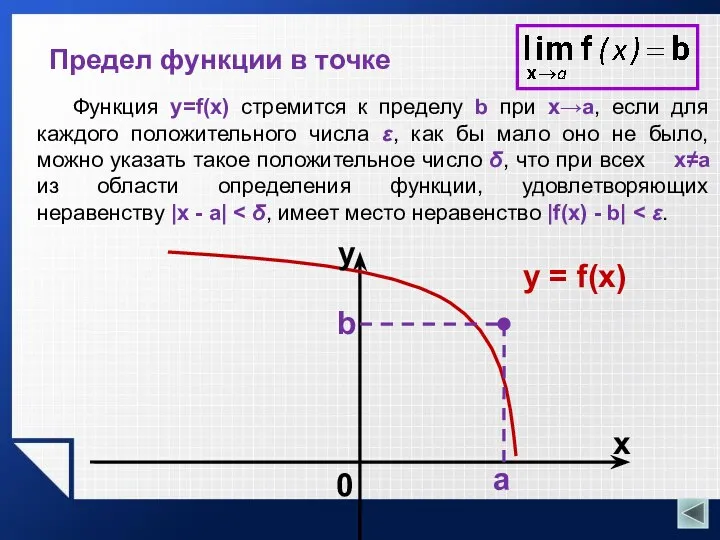
- 16. Предел функции в точке Функция y=f(x) стремится к пределу b при x→a, если для каждого положительного
- 18. Скачать презентацию














 Применение различных способов разложения на множители многочлена
Применение различных способов разложения на множители многочлена Представляют геометрические фигуры
Представляют геометрические фигуры Матрицы. 1 часть
Матрицы. 1 часть Презентация на тему Числовые неравенства и их свойства
Презентация на тему Числовые неравенства и их свойства  Случаи сложения вида +5
Случаи сложения вида +5 Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Формирование алгоритмического мышления у младших школьников
Формирование алгоритмического мышления у младших школьников Формула Пика
Формула Пика Перпендикулярность плоскостей
Перпендикулярность плоскостей Математика. Раздел 6. Метод координат в пространстве. Занятие 63. Координаты точек и векторов
Математика. Раздел 6. Метод координат в пространстве. Занятие 63. Координаты точек и векторов П.Л. Чебышёв – гордость русской науки. Занятие математического кружка в 8-9 классах
П.Л. Чебышёв – гордость русской науки. Занятие математического кружка в 8-9 классах Линейная алгебра и аналитическая геометрия
Линейная алгебра и аналитическая геометрия Математический марафон. Интеллектуальная игра
Математический марафон. Интеллектуальная игра Тригонометрия. Меры углов. Определения синуса, косинуса, тангенса, котангенса
Тригонометрия. Меры углов. Определения синуса, косинуса, тангенса, котангенса Задания с фигурами
Задания с фигурами Алгебра в жизни человека
Алгебра в жизни человека Презентация на тему Арифметическая прогрессия: практикум
Презентация на тему Арифметическая прогрессия: практикум 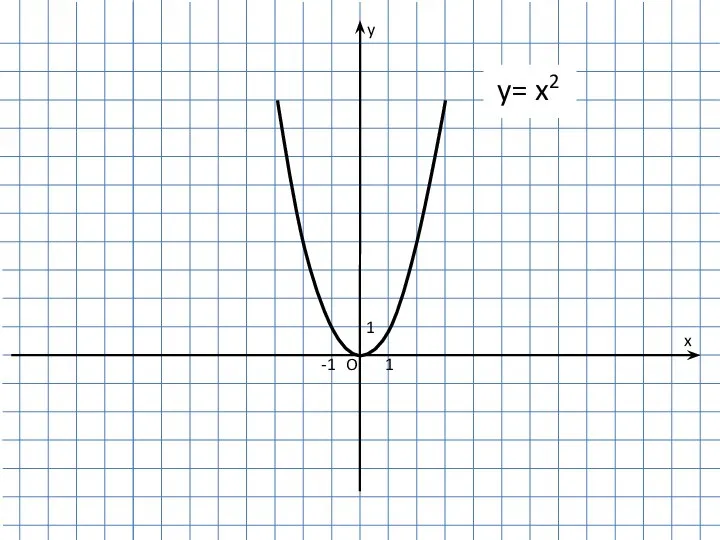 Функция y= x2
Функция y= x2 Семь чудес Кузбасса 5 класс
Семь чудес Кузбасса 5 класс Неравенство треугольника (7 класс)
Неравенство треугольника (7 класс) Формулы сокращенного умножения. Космический час на планете знаний
Формулы сокращенного умножения. Космический час на планете знаний Теория множеств
Теория множеств Многоугольники
Многоугольники Уравнение линии на плоскости
Уравнение линии на плоскости Сложение вида +2 +3 с переходом через десяток
Сложение вида +2 +3 с переходом через десяток Презентация на тему НАХОЖДЕНИЕ ЧИСЛА ПО ЕГО ДРОБИ
Презентация на тему НАХОЖДЕНИЕ ЧИСЛА ПО ЕГО ДРОБИ  Прибавить и вычесть число 1
Прибавить и вычесть число 1 Площади и объемы многогранников. Решение задач
Площади и объемы многогранников. Решение задач