Содержание
- 2. матрицы Определение матрицы Виды матрицы Равенство матриц Сложение матриц Умножение матрицы на число Умножение матриц
- 3. Определение матрицы Прямоугольная таблица, составленная из m x n чисел, называется матрицей. Для обозначения матрицы применяются
- 4. Горизонтальные ряды матрицы называются строками матрицы вертикальные - столбцами. Индексы i и j элемента aij, где
- 5. Виды матриц Квадратная матрица Диагональная матрица Единичная матрица Матрица-строкаМатрица-строка Матрица-строка и матрица-столбец Транспонированная матрица
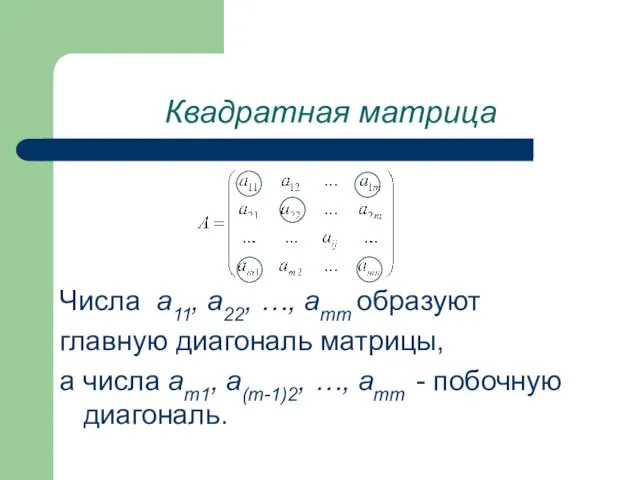
- 6. Квадратная матрица Матрица, у которой число строк равно числу ее столбцов называется квадратной матрицей. При этом
- 7. Числа a11, a22, …, amm образуют главную диагональ матрицы, а числа am1, a(m-1)2, …, amm -
- 8. Диагональная матрица Квадратная матрица, у которой все числа, не стоящие на главной диагонали, равны нулю, называется
- 9. ЕДИНИЧНАЯ МАТРИЦА Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной матрицей. Единичную
- 10. Матрица-строка Матрица, состоящая только из одной строки, называется матрицей-строкой. Матрица, состоящая только из одной строки, называется
- 11. Транспонированная матрица Матрица называется транспонированной по отношению к матрице А, если столбцы матрицы являются соответствующими строчками
- 12. РАВЕНСТВО МАТРИЦ Две матрицы А и В называются равными (A=B), если они имеют одинаковые размеры и
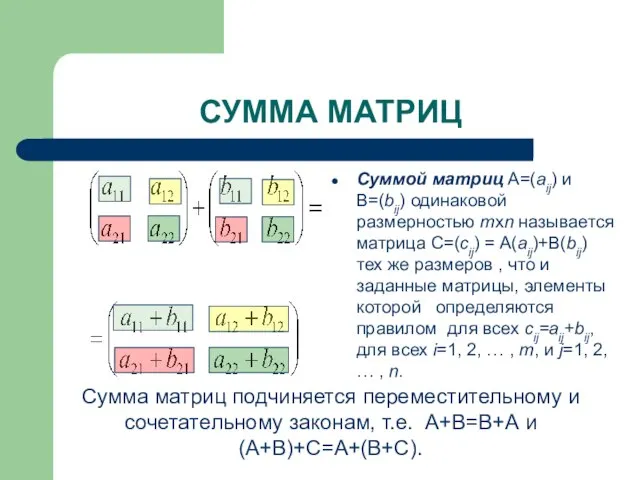
- 13. СУММА МАТРИЦ Суммой матриц A=(aij) и B=(bij) одинаковой размерностью mxn называется матрица С=(cij) = A(aij)+B(bij) тех
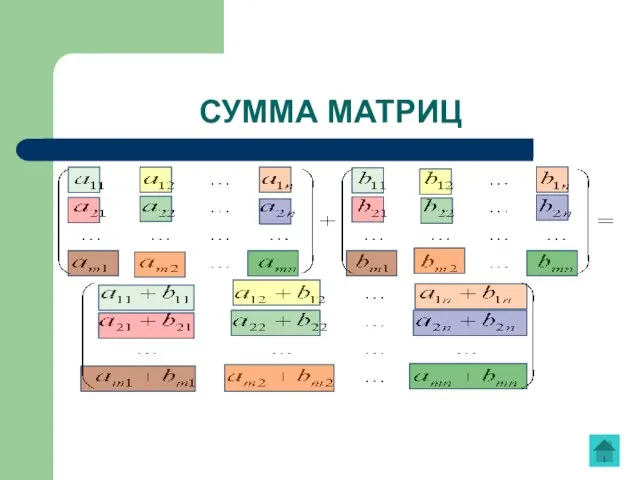
- 14. СУММА МАТРИЦ
- 15. Умножение матрицы на число Произведением матрицы A=(aij) размеров mxn на число k называется матрица B=(bij) тех
- 16. УМНОЖЕНИЕ МАТРИЦ Пусть заданы матрица А размеров mxn и матрица В размеров nxp, т.е. такие, что
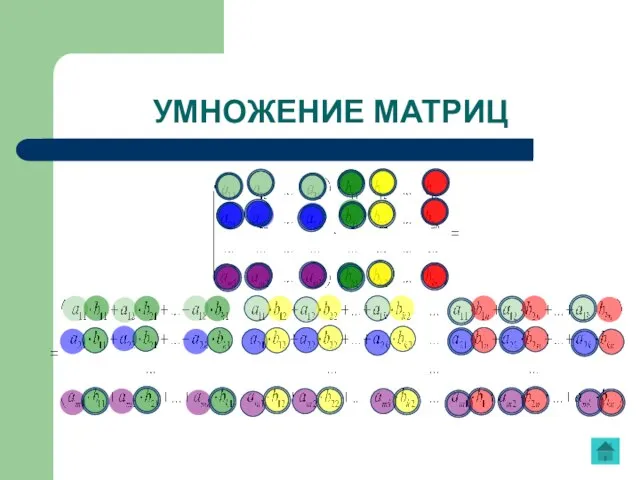
- 17. Произведением матрицы А размеров mxn на матрицу В размеров nxp называется матрица размеров mxp , элементы
- 18. УМНОЖЕНИЕ МАТРИЦ
- 20. Скачать презентацию













 Подготовка к ЕГЭ
Подготовка к ЕГЭ Числа и точки на прямой
Числа и точки на прямой Величины. Объём
Величины. Объём Шахматы и математика
Шахматы и математика Окружности. Центр окружности
Окружности. Центр окружности Презентация на тему Леонтий Филиппович Магницкий
Презентация на тему Леонтий Филиппович Магницкий  Логические основы обработки информации. Алгебра логики
Логические основы обработки информации. Алгебра логики Признаки параллельности двух прямых
Признаки параллельности двух прямых Вычисление вероятностей по электроснабжению
Вычисление вероятностей по электроснабжению Числовые последовательности
Числовые последовательности Площади фигур
Площади фигур Линейные дискретные системы с постоянными параметрами. Лекция 6
Линейные дискретные системы с постоянными параметрами. Лекция 6 Занимательная математика. Задачи в стихах (1 класс)
Занимательная математика. Задачи в стихах (1 класс) Линейная функция и ее график. Прямая пропорциональность
Линейная функция и ее график. Прямая пропорциональность Признаки равенства треугольников
Признаки равенства треугольников Работа над ошибками СОР. Подготовка к СОЧ
Работа над ошибками СОР. Подготовка к СОЧ Решение задач с помощью уравнений. 7 класс
Решение задач с помощью уравнений. 7 класс РўР’РёРњРЎ_Лекция 4_Дискретные СЃРучайные РІРµРичины
РўР’РёРњРЎ_Лекция 4_Дискретные СЃРучайные РІРµРичины Поворот и параллельный перенос
Поворот и параллельный перенос Геометрия
Геометрия Применение производной к исследованию функций и построению графиков
Применение производной к исследованию функций и построению графиков Расстояние от точки до плоскости
Расстояние от точки до плоскости Опыт по получению тени от различных фигур
Опыт по получению тени от различных фигур Функцияның нүктедегі шегі туралы ұғым және функцияның үзіліссіздігі
Функцияның нүктедегі шегі туралы ұғым және функцияның үзіліссіздігі Знакомство с клеткой
Знакомство с клеткой Организации проектной деятельности
Организации проектной деятельности Задачи на увеличение и уменьшение
Задачи на увеличение и уменьшение Системы счисления
Системы счисления