Содержание
- 2. Логарифмическим неравенством называется неравенство, в котором переменная находится под знаком логарифма Логарифмическими неравенствами называют неравенства вида
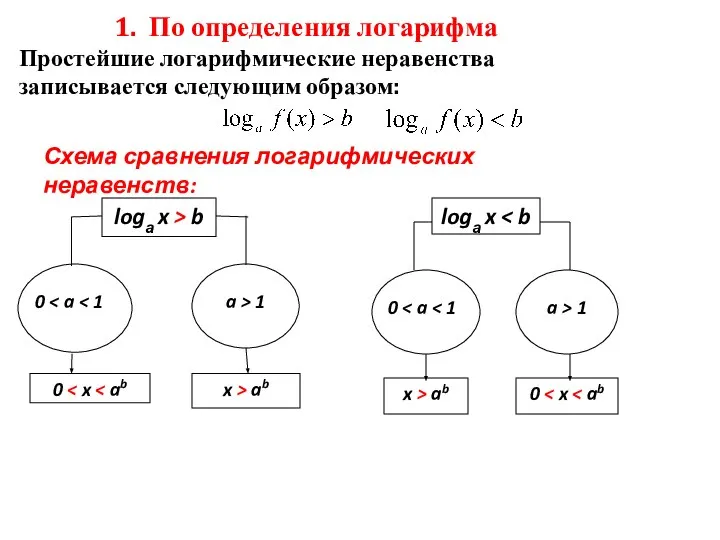
- 3. 1. По определения логарифма Простейшие логарифмические неравенства записывается следующим образом: Схема сравнения логарифмических неравенств:
- 5. 2. Метод потенцирования Суть метода в следующем: с помощью формул неравенство привести к виду Справедливы следующие
- 8. 3).
- 10. log8 (5х-10) 5x-10 6x x Ответ: х (-∞; 4). Решить верно: log8 (5х-10) Ответ: х (2;4).
- 11. 3.Метод введения новой переменной: Ищем в неравенстве некоторое повторяющееся выражение, которое обозначим новой переменной, тем самым,
- 12. Решить неравенство
- 13. Физминутка для глаз
- 14. Правильному применению методов можно научиться, только применяя их на различных примерах Цейтен
- 16. Скачать презентацию

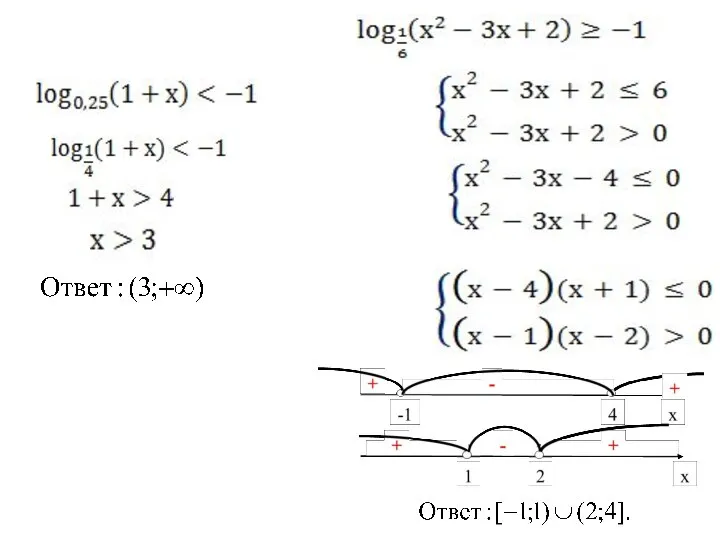



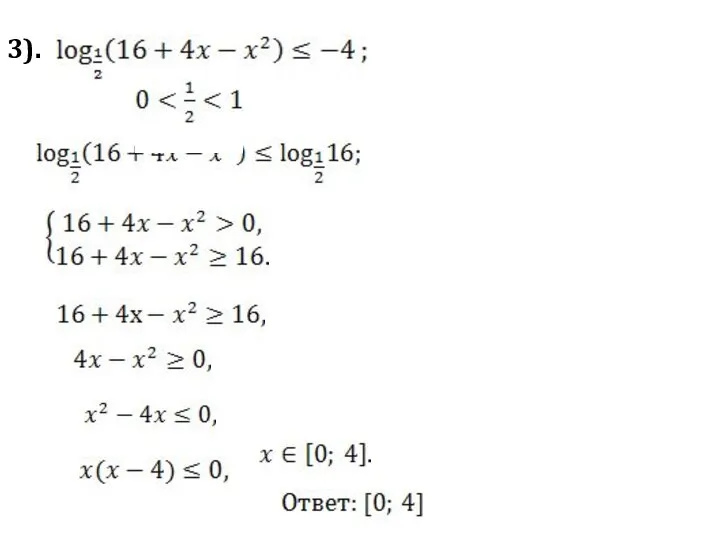



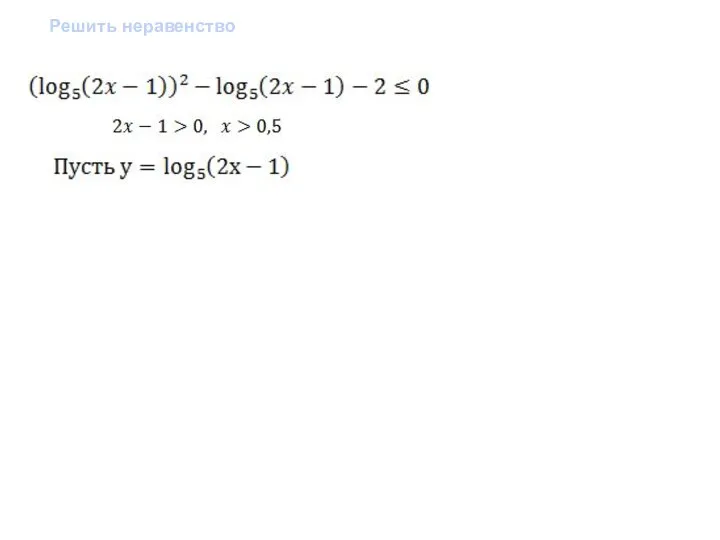

 Некоторые законы распределения случайных величин. Нормальный закон распределения (закон Гаусса)
Некоторые законы распределения случайных величин. Нормальный закон распределения (закон Гаусса) Математика. Занятие 31
Математика. Занятие 31 Подобные треугольники. (8 класс)
Подобные треугольники. (8 класс) Числа 6 и 7. Письмо цифры 7 (1 класс)
Числа 6 и 7. Письмо цифры 7 (1 класс) Эквивалентные преобразования формул
Эквивалентные преобразования формул Численные методы решения систем линейных уравнений
Численные методы решения систем линейных уравнений Косинусоида. Задание № 9
Косинусоида. Задание № 9 Проценты. ОГЭ и ЕГЭ
Проценты. ОГЭ и ЕГЭ Треугольники. Задачи
Треугольники. Задачи Решение СЛАУ методом Крамера
Решение СЛАУ методом Крамера Средняя линия треугольника (8 класс)
Средняя линия треугольника (8 класс) Устный счёт для дошкольников
Устный счёт для дошкольников Десятичные дроби произвольного знака
Десятичные дроби произвольного знака Вычитание смешанных чисел. 5 класс
Вычитание смешанных чисел. 5 класс Арифметический пейзаж
Арифметический пейзаж электронный учебник по интеллектике в 5 классе. знакомство с вероятностью
электронный учебник по интеллектике в 5 классе. знакомство с вероятностью Приближенные решения уравнений
Приближенные решения уравнений Цикл for
Цикл for Вторая производная и её физический смысл
Вторая производная и её физический смысл Max cut problem
Max cut problem Третий признак равенства треугольников. 7 класс
Третий признак равенства треугольников. 7 класс Тригонометрия (В5, В7) на ЕГЭ
Тригонометрия (В5, В7) на ЕГЭ Играем и считаем. Комплекс учебно-развивающих компьютерных игровых тренажеров по начальному обучению математике
Играем и считаем. Комплекс учебно-развивающих компьютерных игровых тренажеров по начальному обучению математике Параллельные прямые
Параллельные прямые Задача на арифметическую прогрессию (2)
Задача на арифметическую прогрессию (2)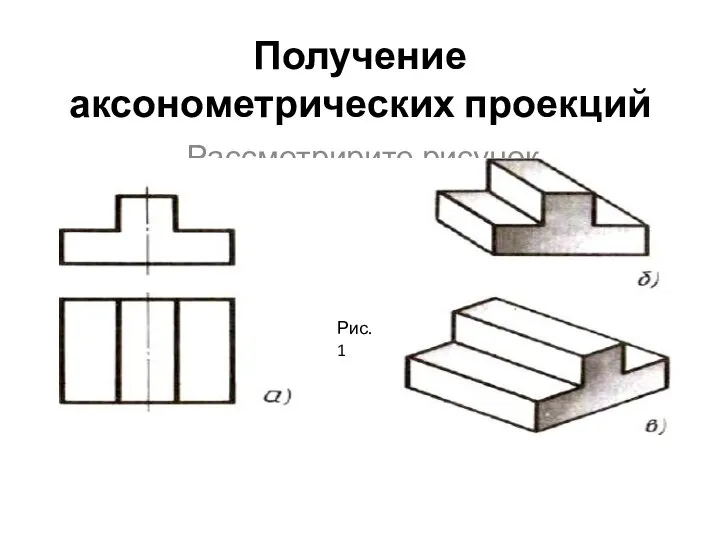 Получение аксонометрических проекций
Получение аксонометрических проекций Движение
Движение Виды кривых, замечательные кривые. Окружность и круг
Виды кривых, замечательные кривые. Окружность и круг