Решение неравенств методом интервалов

Содержание
Пример 1.
Пример 2.
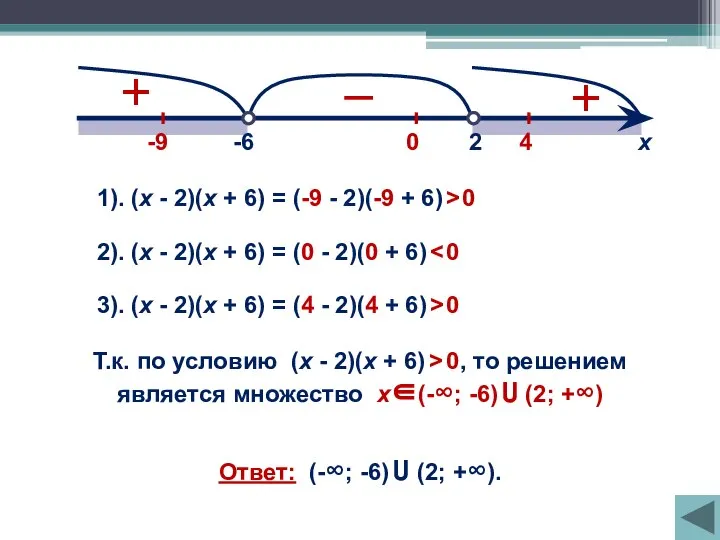
Пример 3.

Пример 1. Решить неравенство: (х - 2)(х + 6) > 0
Найдём корни квадратного трехчлена из уравнения:
(х – 2)(х + 6) = 0
х1 = 2; х2 = -6
Отметим эти корни на числовой прямой:
2
-6
х
Получим три промежутка:
Определим знаки (х - 2)(х + 6) на каждом из полученных промежутков:
х – 2 = 0 или х + 6 = 0

2
-6
х
1). (х - 2)(х + 6) = (-9 - 2)(-9 + 6) > 0
-9
2). (х - 2)(х + 6) = (0 - 2)(0 + 6) < 0
0
4
3). (х - 2)(х + 6) = (4 - 2)(4 + 6) > 0
+
+
–
Т.к. по условию (х - 2)(х + 6) > 0, то решением
является множество х∈(-∞; -6) U (2; +∞)
Ответ: (-∞; -6) U (2; +∞).

Пример 2. Решить неравенство: 2х2 - 3х + 1 < 0
Найдём корни квадратного трехчлена из уравнения:
2х2 - 3х + 1 = 0
х1 = 1; х2 = 0,5
Отметим эти корни на числовой прямой:
1
0,5
х
Получим три промежутка:
Определим знаки 2х2 - 3х + 1 на каждом из полученных промежутков:

+
1
0,5
х
1). 2х2 - 3х + 1 = 2∙02 - 3∙0 + 1 > 0
0
0,8
1,2
+
–
Т.к. по условию 2х2 - 3х + 1 < 0, то решением
является множество х∈(0,5; 1)
Ответ: (0,5; 1).
2). 2х2 - 3х + 1 = 2∙0,82 - 3∙0,8 + 1 < 0
3). 2х2 - 3х + 1 = 2∙1,22 - 3∙1,2 + 1 > 0

Пример 3. Решить неравенство: -х2 + х + 12 ≥ 0
Найдём корни квадратного трехчлена из уравнения:
-х2 + х + 12 = 0
х1 = 4; х2 = -3
Отметим эти корни на числовой прямой:
4
-3
х
Получим три промежутка:
Определим знаки -х2 + х + 12 на каждом из полученных промежутков: