Проверка статистических гипотез. Статистическая функция распределения случайной величины

Учебный вопрос №1 Статистическая функция распределения
случайной величины.

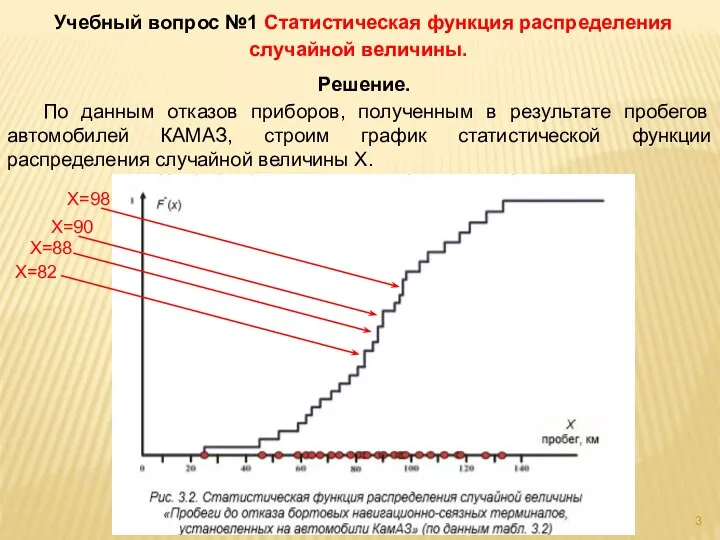
Учебный вопрос №1 Статистическая функция распределения
случайной величины.
Решение.
По данным отказов приборов, полученным в результате пробегов автомобилей КАМАЗ, строим график статистической функции распределения случайной величины Х.
Х=82
Х=88
Х=90
Х=98

Учебный вопрос №2 Точечные оценки параметров
функции распределения случайной величины.
2.1 Основные определения.

2.2 Нахождение точечной оценки математического ожидания
случайной величины по данным выборки.

2.3 Нахождение точечной оценки дисперсии, среднего квадратичного отклонения и коэффициента вариации случайной величины
по данным выборки
Точечная оценка дисперсии определяется по формуле:

Для нормально распределенной случайной величины значение коэффициента вариации V должно быть меньше 0,3. Исходя из этого, гипотеза о нормальном законе распределения для случайной величины (пробеги автомобилей КАМАЗ до отказа прибора), правдоподобна.

Учебный вопрос №3 Построение доверительного интервала
для параметров нормального распределения.
3.1 Основные определения.

3.2 Пример построения доверительного интервала.

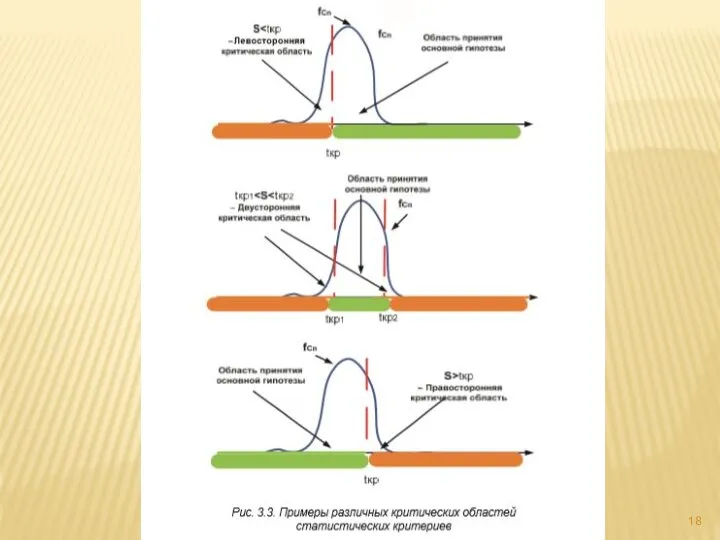
Учебный вопрос №4 Проверка статистических гипотез
4.1 Основные понятия.

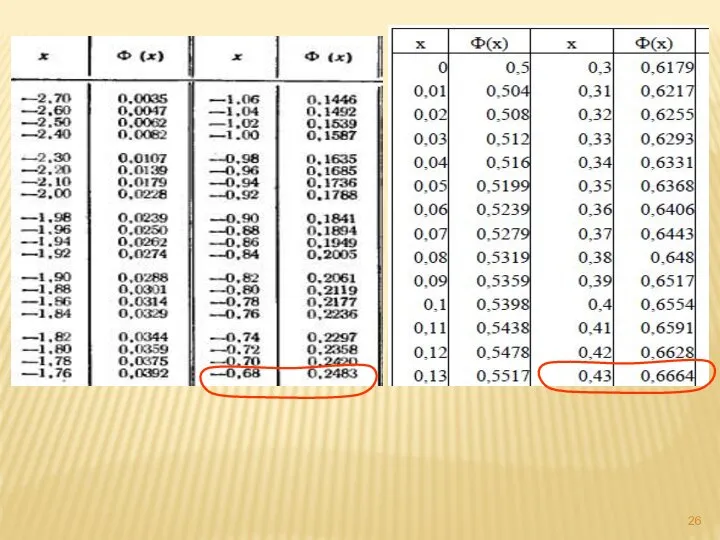
4.2 Проверка гипотез о законе распределения с использованием
критерия Пирсона χ2

4.3 Пример проверки гипотеза о законе распределения

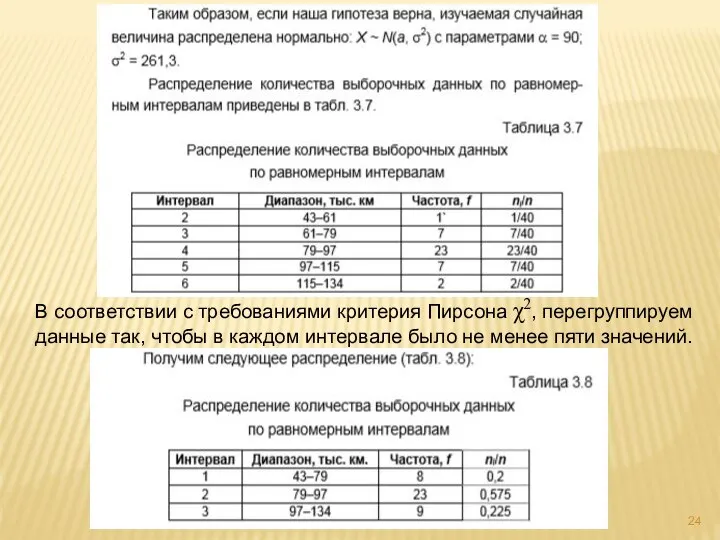
В соответствии с требованиями критерия Пирсона χ2, перегруппируем
данные так, чтобы в каждом интервале было не менее пяти значений.

где из условия примера n=40.