Содержание
- 2. Если выполняется неравенство t >t ℓ , то значение коэффициента корреляции признается значимым, т.е нулевая гипотеза,
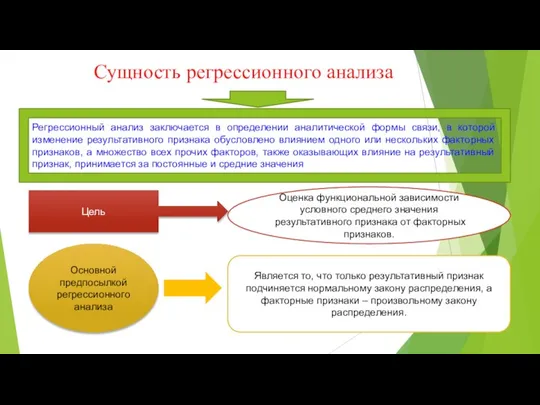
- 3. Сущность регрессионного анализа Регрессионный анализ заключается в определении аналитической формы связи, в которой изменение результативного признака
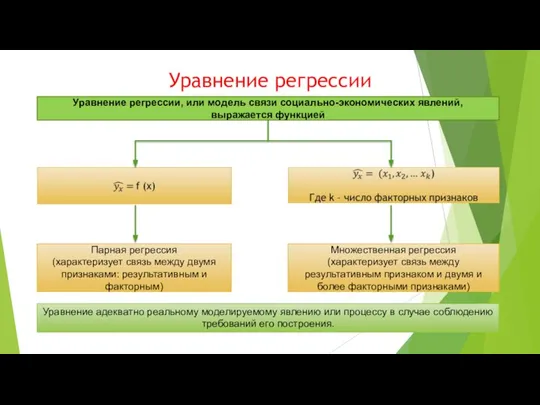
- 4. Уравнение регрессии Уравнение регрессии, или модель связи социально-экономических явлений, выражается функцией Множественная регрессия (характеризует связь между
- 5. Требования к построению уравнения регрессии Совокупность исходных данных должна быть однородной и математически описываться непрерывными функциями
- 6. Теоретическая обоснованность моделей Условия Теоретической Обоснованности моделей
- 7. Уравнение линейной парной регрессии Уравнение линейной парной регрессии Параметры модели и их содержание
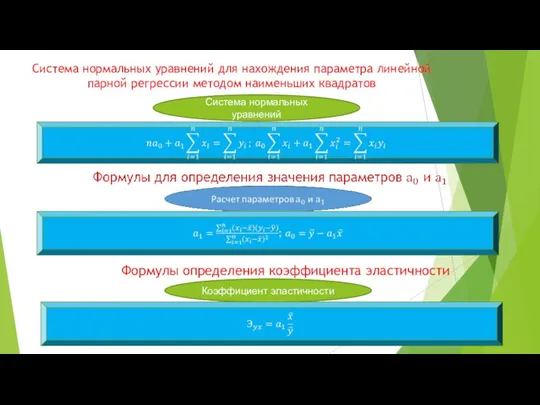
- 8. Система нормальных уравнений для нахождения параметра линейной парной регрессии методом наименьших квадратов Система нормальных уравнений Формулы
- 9. Формула определения бета-коэффициента Бета-коэффициент Важно! Бета-коэффициент показывает, на какую часть своего среднего квадратического отклонения изменится в
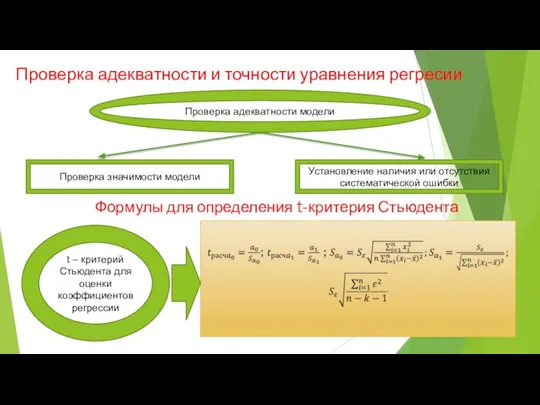
- 10. Формулы для определения t-критерия Стьюдента Проверка адекватности модели Проверка значимости модели Установление наличия или отсутствия систематической
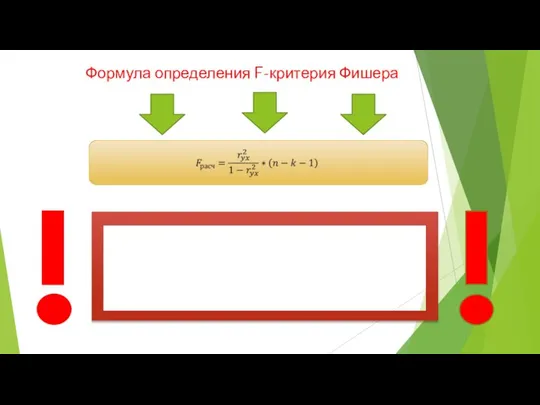
- 11. Формула определения F-критерия Фишера
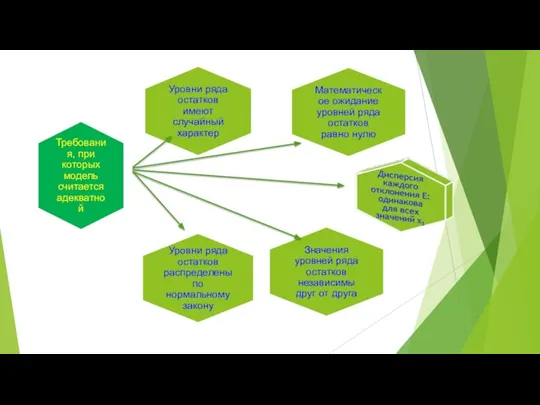
- 13. Соблюдение требований, которым должен удовлетворять ряд остатков
- 17. Скачать презентацию








 Округление.десятичных дробей
Округление.десятичных дробей Теория вероятностей. Задачи ЕГЭ
Теория вероятностей. Задачи ЕГЭ Действия с десятичными дробями
Действия с десятичными дробями Согласование существительных с числительными
Согласование существительных с числительными Презентация по математике "Двоичная арифметика. Сложение Вычитание Умножение" -
Презентация по математике "Двоичная арифметика. Сложение Вычитание Умножение" -  Задание 19. Профиль
Задание 19. Профиль Государственное общеобразовательное учреждение Гимназия№49 Приморского района Санкт -Петербурга «Путешествие Алисы в страну Ма
Государственное общеобразовательное учреждение Гимназия№49 Приморского района Санкт -Петербурга «Путешествие Алисы в страну Ма 2_Teoria_veroyatnostey_920_is
2_Teoria_veroyatnostey_920_is Усеченная пирамида
Усеченная пирамида Взаимосвязь между скоростью, временем и расстоянием. Умножение на числа, оканчивающиеся нулями
Взаимосвязь между скоростью, временем и расстоянием. Умножение на числа, оканчивающиеся нулями Квадратичная функция. Преобразование графика параболы путем параллельного переноса вдоль осей абцисс и ординат
Квадратичная функция. Преобразование графика параболы путем параллельного переноса вдоль осей абцисс и ординат Пропозиційна логика (продовження). Лекція №2
Пропозиційна логика (продовження). Лекція №2 Задачи с дробями
Задачи с дробями Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника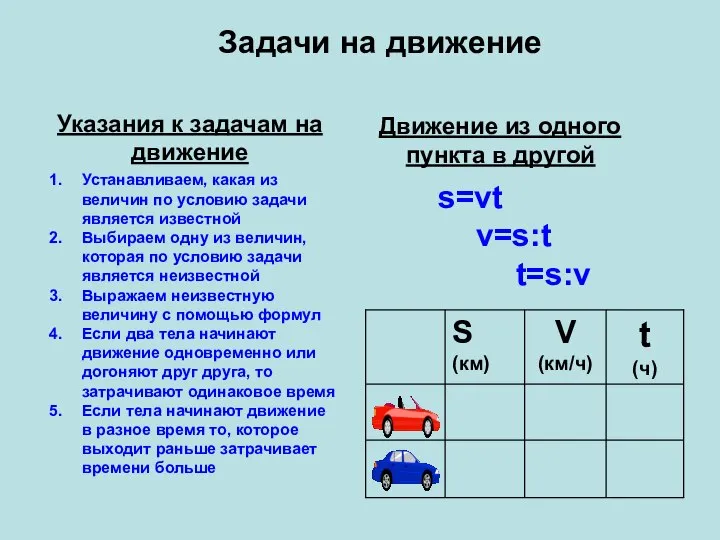 Задачи на движение Указания к задачам на движение
Задачи на движение Указания к задачам на движение Понятие вектора
Понятие вектора Понятие вектора в пространстве
Понятие вектора в пространстве Применение распределительного свойства умножения
Применение распределительного свойства умножения Запомни цифры
Запомни цифры Презентация на тему Квадратичная функция
Презентация на тему Квадратичная функция  Уравнение окружности
Уравнение окружности Моделирование. Объекты и их модели. (Тема 10)
Моделирование. Объекты и их модели. (Тема 10) Взаимное расположение прямых в пространстве. Угол между двумя прямыми
Взаимное расположение прямых в пространстве. Угол между двумя прямыми Aproximarea numerică a funcţiilor. Metode numerice – curs 10
Aproximarea numerică a funcţiilor. Metode numerice – curs 10 Сумма углов треугольника
Сумма углов треугольника Число или цифра 5
Число или цифра 5 Признаки параллельности прямых
Признаки параллельности прямых Задача з піцою
Задача з піцою