Содержание
- 2. 11.1. ПЕРВООБРАЗНАЯ ФУНКЦИИ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Функция F(x) называется первообразной функции f(x) на промежутке Х, если
- 3. Например, функция является первообразной для функции поскольку Для заданной функции f(x) ее первообразная определена не однозначно.
- 4. В общем случае, если F(x) – первообразная для функции f(x), то функция вида F(x)+С тоже является
- 5. Из геометрического смысла производной вытекает, что есть угловой коэффициент касательной к кривой y=F(x) в точке х.
- 6. ТЕОРЕМА. Если F1(x) и F2(x) - первообразные функции f(x) на некотором промежутке Х, то найдется такое
- 7. Доказательство: Найдем производную разности первообразных: Тогда по следствию из теоремы Лагранжа найдется число С, такое что
- 8. Из этой теоремы следует, что если F(x) – первообразная для функции f(x), то выражение задает все
- 9. Совокупность всех первообразных для функции f(x) на промежутке Х называется неопределенным интегралом от функции f(x). Функция
- 11. Скачать презентацию








 Экзаменационные задачи по дисциплине Процессы и аппараты
Экзаменационные задачи по дисциплине Процессы и аппараты Множественные связи. Порядковые и категоризованные переменные
Множественные связи. Порядковые и категоризованные переменные Lecture 6. Techniques of Integration (part 1)
Lecture 6. Techniques of Integration (part 1) Тригонометрия. Подготовка к диагностической работе
Тригонометрия. Подготовка к диагностической работе Изоморфизм понятий
Изоморфизм понятий Сравнение чисел. Координаты
Сравнение чисел. Координаты Проверка математических данных в произведении Н. Носова Незнайка на Луне
Проверка математических данных в произведении Н. Носова Незнайка на Луне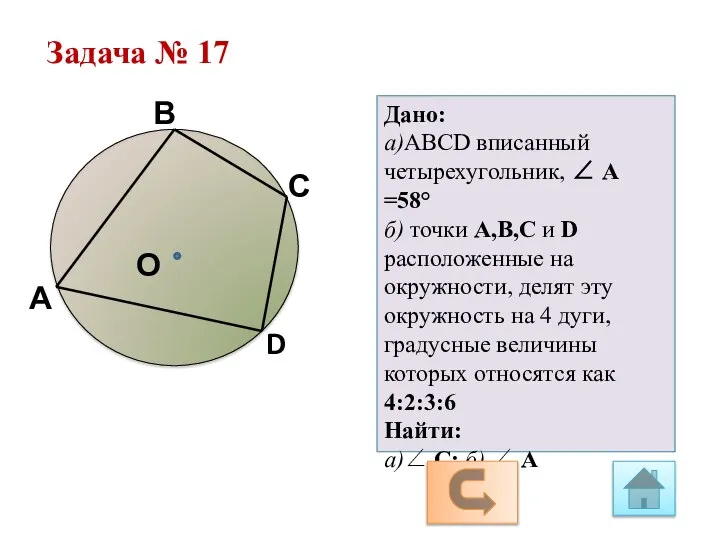 Геометрия 9 класс. Задачи
Геометрия 9 класс. Задачи Тетраэдр и параллелепипед. Геометрия 10 класс
Тетраэдр и параллелепипед. Геометрия 10 класс Понятие системы
Понятие системы Предельные величины, эластичности
Предельные величины, эластичности Приёмы устных вычислений
Приёмы устных вычислений Литература
Литература Системы линейных уравнений
Системы линейных уравнений Структура урока
Структура урока Тела вращения
Тела вращения Арксинус, Арккосинус, Арктангенс, Арккотангенс
Арксинус, Арккосинус, Арктангенс, Арккотангенс Натуральные и целые числа. Проверочная работа
Натуральные и целые числа. Проверочная работа Решение задач по теме Треугольники. 7 класс
Решение задач по теме Треугольники. 7 класс Математическое описание случайных явлений
Математическое описание случайных явлений + - 3. Закрепление. Сравнение отрезков
+ - 3. Закрепление. Сравнение отрезков Классические алгоритмы на графах
Классические алгоритмы на графах Математические знания при покупке телевизора
Математические знания при покупке телевизора Решение систем неравенств с одной переменной
Решение систем неравенств с одной переменной Математика. Задачи на кратное сравнение
Математика. Задачи на кратное сравнение Углы. Прямой и развернутый углы
Углы. Прямой и развернутый углы Логарифмы. История возникновения логарифмов
Логарифмы. История возникновения логарифмов Элементы аналитической геометрии на плоскости
Элементы аналитической геометрии на плоскости