Слайд 2Повторение:
1. Что является графиком линейного уравнения с двумя неизвестными?
2.Что называется системой двух

линейных уравнений с двумя переменными?
3.Что называется решением системы?
4.Что значит решить систему двух линейных уравнений с двумя неизвестными?
Слайд 3Метод сложения
Решим систему уравнений:
1) Сложим почленно уравнение (1)
и уравнение (2)

Слайд 4Метод сложения
2) Упрощаем
3) Решаем уравнение:

Слайд 5Метод сложения
4) Подставим в уравнение (1) получившееся значение аргумента x
5) Решаем уравнение

Слайд 6Метод сложения
Таким образом решением системы уравнений:
Является пара чисел:

Слайд 7Метод сложения
Решим систему уравнений:
Умножим уравнение (1) на число - 2

Слайд 9Метод сложения
1) Сложим почленно уравнение (1)
и уравнение (2)
2) Упрощаем

Слайд 10Метод сложения
4) Подставим в уравнение (2) получившееся значение y
3) Решаем уравнение:

Слайд 11Метод сложения
5) Решаем уравнение

Слайд 12Метод сложения
Таким образом решением системы уравнений:
Является пара чисел:

Слайд 13Способ сложения (алгоритм)
Уравнять модули коэффициентов при какой-нибудь переменной
Сложить почленно уравнения системы
Составить новую

систему: одно уравнение новое, другое - одно из старых
Решить новое уравнение и найти значение одной переменной
Подставить значение найденной переменной в старое уравнение и найти значение другой переменной
Записать ответ: х=…; у=… .
Слайд 14Решение системы способом сложения
||·(-3)
+
____________
Ответ: (3; - 10)














 Решение заданий ЕГЭ уровня С2 (1 часть)
Решение заданий ЕГЭ уровня С2 (1 часть) Сочетательное и распределительное свойство умножения. Урок 1
Сочетательное и распределительное свойство умножения. Урок 1 Признаки делимости на 2, 5,10, 3, 6 и 9
Признаки делимости на 2, 5,10, 3, 6 и 9 Параллельные прямые в пространстве
Параллельные прямые в пространстве Неопределенный интеграл
Неопределенный интеграл Урок 53. Расстояние от точки до прямой
Урок 53. Расстояние от точки до прямой Степень с рациональным показателем
Степень с рациональным показателем Косинус угла
Косинус угла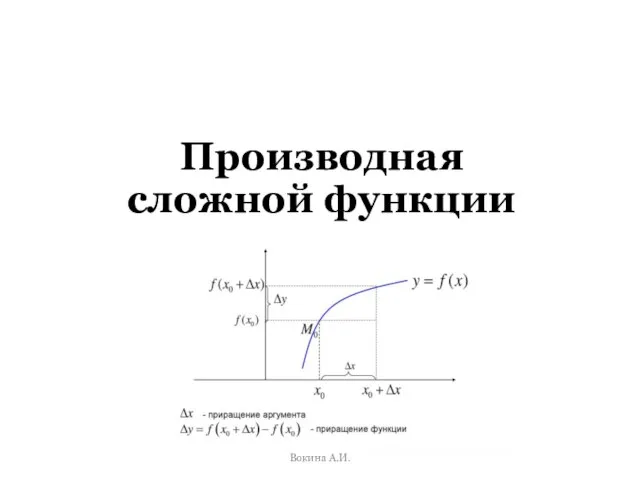 Производная сложной функции
Производная сложной функции Понятие вектора
Понятие вектора Определители. Матрица и ее определитель
Определители. Матрица и ее определитель Решение простейших тригонометрических уравнений с помощью единичной окружности
Решение простейших тригонометрических уравнений с помощью единичной окружности Задания на развитие логики
Задания на развитие логики 20171212_prezentatsiya_k_urokuарифметические действия над обыкновенными дробями и смешанными числами
20171212_prezentatsiya_k_urokuарифметические действия над обыкновенными дробями и смешанными числами Деловая игра Маркетинг инноваций
Деловая игра Маркетинг инноваций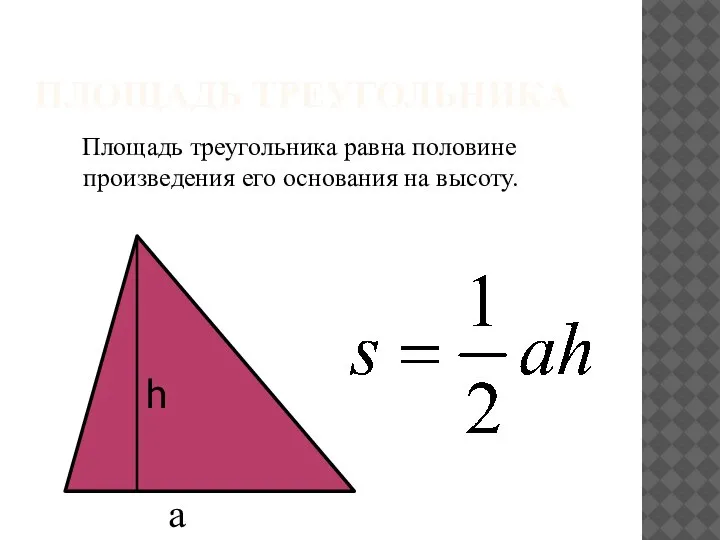 Площадь треугольника
Площадь треугольника Математика без границ. Конкурс
Математика без границ. Конкурс Сантиметр. Линейка
Сантиметр. Линейка Золотое сечение
Золотое сечение Информатика. Вероятность
Информатика. Вероятность Загадки и тайны треугольника
Загадки и тайны треугольника Сложение вида + 2, + 3
Сложение вида + 2, + 3 Презентация на тему Признаки равенства треугольников
Презентация на тему Признаки равенства треугольников  Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике)
Производная. Первообразная. Интеграл (по материалам открытого банка задач ЕГЭ по математике) Умножение одночлена на многочлен
Умножение одночлена на многочлен Современная финансовая математика
Современная финансовая математика Элементы круга и окружности в задачах ОГЭ
Элементы круга и окружности в задачах ОГЭ Плоскость и прямая в пространстве
Плоскость и прямая в пространстве