Содержание
- 2. Одной из наиболее важных тем курса алгебры является решение систем линейных уравнений Есть несколько видов решения
- 3. Решение системы линейных уравнений методом почленного сложения (вычитания) уравнений системы
- 4. Суть данного метода состоит в избавлении от одной из переменных в системе уравнений, алгоритм метода достаточно
- 5. В качестве примера решим систему уравнений: методом почленного сложения (вычитания). Здесь будет достаточно просто «избавиться» от
- 6. Получим равносильную систему уравнений: Теперь прибавим к левой части первого уравнения левую часть второго уравнения, а
- 7. Решим это уравнение относительно единственной переменной: Подставим найденное значение в первое уравнение исходной системы и найдём
- 8. Решите систему линейных уравнений: Х – У + 5 = 0 2Х + У + 7
- 9. Анализируя систему уравнений, замечаем, что коэффициенты при переменной y одинаковы по модулю и противоположны по знаку
- 10. В чистовом оформлении решение должно выглядеть примерно так: Ответ: x = -4, y = 1
- 12. Скачать презентацию









 Решение систем неравенств с одной переменной. 8 класс
Решение систем неравенств с одной переменной. 8 класс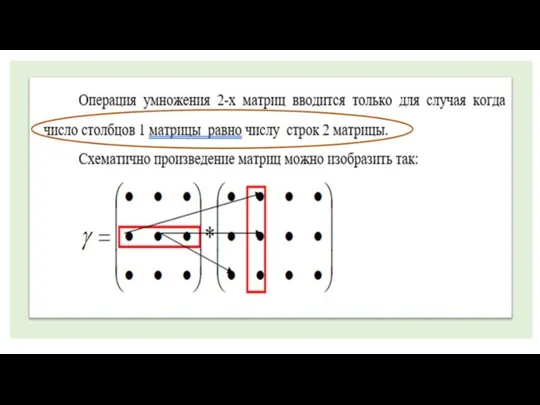 Операция умнодения 2 матриц
Операция умнодения 2 матриц Один - много. 1 класс
Один - много. 1 класс Веселый счет. Викторина
Веселый счет. Викторина Уравнение окружности
Уравнение окружности Подмножество. Операции над множествами. Самостоятельная работа
Подмножество. Операции над множествами. Самостоятельная работа Фундаментальные и прикладные исследования в метрологии
Фундаментальные и прикладные исследования в метрологии Общее решение неполного квадратного уравнения. 8 класс
Общее решение неполного квадратного уравнения. 8 класс Длиннее, короче (1 класс)
Длиннее, короче (1 класс) Языки и автоматы
Языки и автоматы Знаки неравенств. Историческая справка
Знаки неравенств. Историческая справка Как измерить величину угла
Как измерить величину угла Rinjka liinija
Rinjka liinija Цилиндр
Цилиндр Правила деления. (6 класс)
Правила деления. (6 класс) Занятие 45. Формулы двойного угла. Формулы половинного угла
Занятие 45. Формулы двойного угла. Формулы половинного угла Комбинаторные методы решения вероятностных задач
Комбинаторные методы решения вероятностных задач Вычисление производных с помощью правил дифференцирования
Вычисление производных с помощью правил дифференцирования Пирамида
Пирамида Понятие множество
Понятие множество Расчет количества потолочной краски
Расчет количества потолочной краски Презентация на тему ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ
Презентация на тему ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ  Формулы сложения
Формулы сложения Сложение сил. Лабораторная работа №5
Сложение сил. Лабораторная работа №5 Прогрессия. Задача
Прогрессия. Задача Арифметические действия с десятичными дробями. Математический тренажёр
Арифметические действия с десятичными дробями. Математический тренажёр Lektsia-2-russ
Lektsia-2-russ Правильные многогранники
Правильные многогранники