- Главная
- Математика
- Производная функции

Содержание
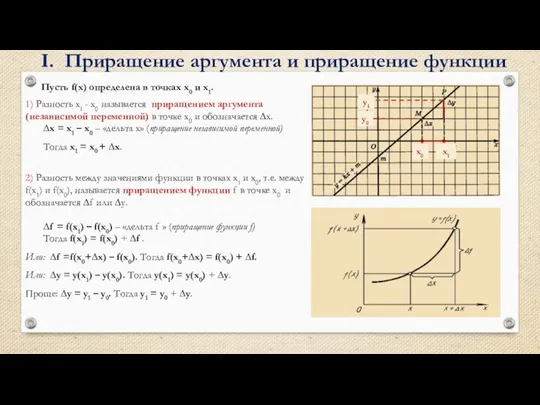
- 2. I. Приращение аргумента и приращение функции Пусть f(х) определена в точках х0 и х1. х1 х0
- 3. I. Приращение аргумента и приращение функции ∆х = х1 – х0 х1 = х0 + ∆х
- 4. I. Приращение аргумента и приращение функции ∆х = х1 – х0 х1 = х0 + ∆х
- 5. I. Приращение аргумента и приращение функции ∆х = х1 – х0 х1 = х0 + ∆х
- 7. Скачать презентацию
Слайд 2 I. Приращение аргумента и приращение функции
Пусть f(х) определена в точках х0
I. Приращение аргумента и приращение функции
Пусть f(х) определена в точках х0
х1
х0
2) Разность между значениями функции в точках х1 и х0, т.е. между f(х1) и f(х0), называется приращением функции f в точке x0 и обозначается ∆f или ∆у.
∆f = f(х1) – f(х0) – «дельта f » (приращение функции f)
Тогда f(х1) = f(х0) + ∆f .
Или: ∆f =f(х0+∆х) – f(х0). Тогда f(х0+∆х) = f(х0) + ∆f.
Или: ∆у = у(х1) – у(х0). Тогда у(х1) = у(х0) + ∆у.
Проще: ∆у = у1 – у0. Тогда у1 = у0 + ∆у.
1) Разность х1 - х0 называется приращением аргумента (независимой переменной) в точке х0 и обозначается ∆х.
∆х = х1 – х0 – «дельта х» (приращение независимой переменной)
Тогда х1 = х0 + ∆х.
у0
у1
Слайд 3 I. Приращение аргумента и приращение функции
∆х = х1 – х0
х1
I. Приращение аргумента и приращение функции
∆х = х1 – х0
х1

3) Основные формулы
∆f = f(х1) – f(х0)
f(х1) = f(х0) + ∆f
∆f =f(х0+∆х) – f(х0)
f(х0+∆х) = f(х0) + ∆f
∆у = у1 – у0
у1 = у0 + ∆у
Примеры.
Дано: у = х2 – 1, х0 = 0, х1 = 0,1.
Найти: приращения аргумента и функции.
Решение:
∆х = х1 – х0
∆х = 0,1 – 0 = 0,1
2) ∆у = у(х1) – у(х0 )
∆у = (0,12 – 1) – (02 – 1)= 0,01 – 1 + 1 = 0,01
Слайд 4 I. Приращение аргумента и приращение функции
∆х = х1 – х0
х1
I. Приращение аргумента и приращение функции
∆х = х1 – х0
х1

3) Основные формулы
∆f = f(х1) – f(х0)
f(х1) = f(х0) + ∆f
∆f =f(х0+∆х) – f(х0)
f(х0+∆х) = f(х0) + ∆f
∆у = у1 – у0
у1 = у0 + ∆у
Примеры.
Слайд 5 I. Приращение аргумента и приращение функции
∆х = х1 – х0
х1
I. Приращение аргумента и приращение функции
∆х = х1 – х0
х1

3) Основные формулы
∆f = f(х1) – f(х0)
f(х1) = f(х0) + ∆f
∆f =f(х0+∆х) – f(х0)
f(х0+∆х) = f(х0) + ∆f
∆у = у1 – у0
у1 = у0 + ∆у
Примеры.
 Презентация на тему Задачи на уменьшение (3 класс)
Презентация на тему Задачи на уменьшение (3 класс)  Свойства логарифмов
Свойства логарифмов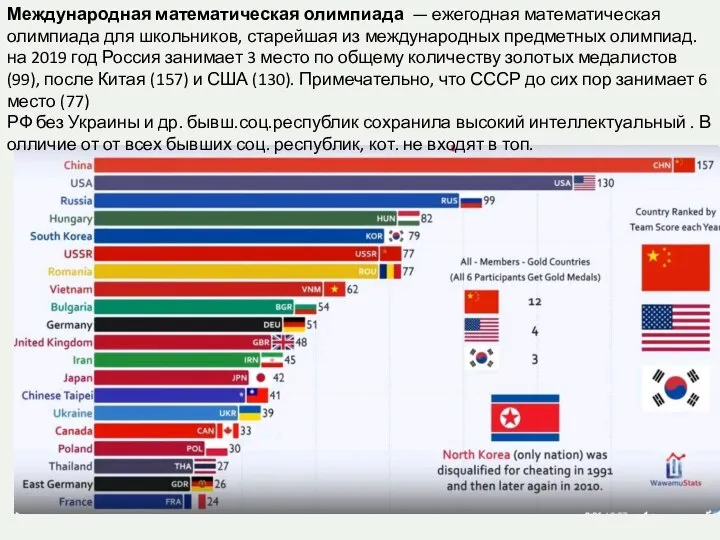 Международная математическая олимпиада
Международная математическая олимпиада Решение текстовых задач. Интегрированный урок с использованием дидактической игры. 9 класс
Решение текстовых задач. Интегрированный урок с использованием дидактической игры. 9 класс Презентация на тему Медиана, биссектриса и высота треугольника
Презентация на тему Медиана, биссектриса и высота треугольника  Роль и место математики в современном мире. Пределы. Свойства пределов. Тема 1.1
Роль и место математики в современном мире. Пределы. Свойства пределов. Тема 1.1 Доли и дроби. 5 класс Новоселова Е.А. МКОУ «Усть-Мосихинская СОШ»
Доли и дроби. 5 класс Новоселова Е.А. МКОУ «Усть-Мосихинская СОШ» Решение треугольников
Решение треугольников Геометрия (8 класс)
Геометрия (8 класс) Скрещивающиеся прямые
Скрещивающиеся прямые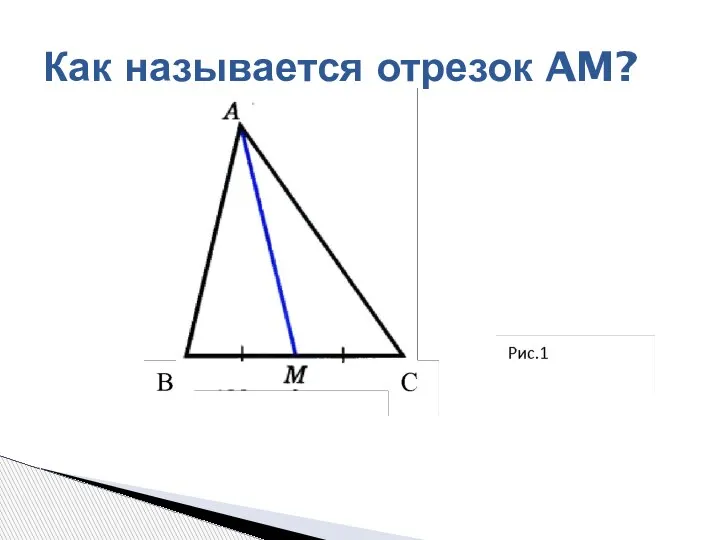 Как называется отрезок AM?
Как называется отрезок AM? Цифра 3. Урок математики в 1 классе
Цифра 3. Урок математики в 1 классе Занимательная математика
Занимательная математика Математическая сказка. Путешествие в сказку Царевна-лягушка
Математическая сказка. Путешествие в сказку Царевна-лягушка Презентация на тему Сложение и вычитание смешанных чисел
Презентация на тему Сложение и вычитание смешанных чисел  Презентация на тему Умножение многочлена на многочлен
Презентация на тему Умножение многочлена на многочлен  Презентация на тему Правильные и неправильные дроби
Презентация на тему Правильные и неправильные дроби  Угол между векторами
Угол между векторами Описанная окружность. 8 класс
Описанная окружность. 8 класс Презентация на тему Параллелограмм. Свойства параллелограмма
Презентация на тему Параллелограмм. Свойства параллелограмма  Правила построения алгоритма
Правила построения алгоритма Система уравнений. Метод алгебраического сложения
Система уравнений. Метод алгебраического сложения Структурные средние величины. Мода и медиана
Структурные средние величины. Мода и медиана Методы решения Слау. Метод Гаусса
Методы решения Слау. Метод Гаусса Графический метод решения систем уравнений
Графический метод решения систем уравнений Решение задач по теме Площади фигур
Решение задач по теме Площади фигур Презентация на тему Буквенные выражения (2 класс)
Презентация на тему Буквенные выражения (2 класс)  ЕГЭ 2014. Задачи первой и второй части (Вариант 43)
ЕГЭ 2014. Задачи первой и второй части (Вариант 43)